LeetCode 5955. 摘水果 题目解析

LeetCode 5955. 摘水果 ⭐️⭐️⭐️⭐️⭐️

5955. 摘水果 #前缀和 #二分查找

1、题目解析

这是LeetCode周赛中的最后一题，也是我觉得迄今为止离AC最近的一次

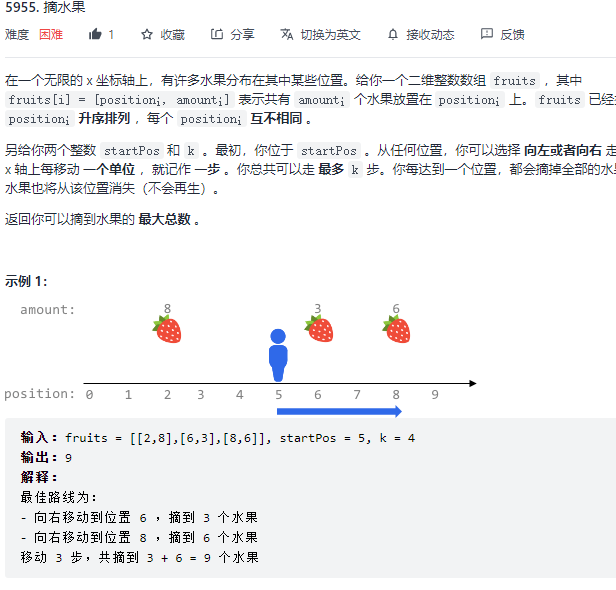
题目很好理解，在最多K次的移动中获取水果的最大值将其返回。

开始的思路是动态规划还有搜索，但是限于水平有限也没有动规出啥东西反而时间浪费了

这道题的核心是要理解：移动的过程中最多改变一次移动的方向

也就是说只要枚举出坐标轴中所有的水果 改变方向前、改变方向后的最大总数之和就是我们需要求的值。

例如水果分别在0、6、7位置上出发点为3，k=10

假设在0出改变方向，出发点到0位置需要3步剩余7，改变位置后人物只会向右方移动，移动的最远距离为7，途中可以采集位于6的水果。在6、7处改变方向也同理，这里不过多赘述。

那么如何快速获取在 移动到某点能收获的数量呢？每一次经过水果后相加时间复杂度高得吓人，这里可以使用前缀和数组，通过前缀和性质能够快速获得值。

那么如何获取每次转向后最终能够收集的水果索引呢？因为索引编号递增，因此可以使用二分查找的方式。如下代码中定义了upperBound查找第一个大于key的索引下标，lowerBound查找第一个大于等于key的索引下标。

因此在代码中，所有的移动方式，先向右移动然后返回向左或先向左移动返回后向右，保存每次移动后获得的最大值，即使答案。

2、代码

class Solution {
    public int upperBound(int []pos,int l,int r,int key){
        while(l<r){
            int m = (l+r)/2;
            if(pos[m]>key){
                r=m;
            }
            else{
                l=m+1;
            }
        }
        return  l;
    }
    public int lowerBound(int []pos,int l,int r,int key){
        while(l<r){
            int m = (l+r)/2;
            if(pos[m]>=key){
                r=m;
            }
            else{
                l=m+1;
            }
        }
        return l;
    }
    public int maxTotalFruits(int[][] fruits, int startPos, int k) {
        List<Integer>sum=new ArrayList<>();
        int ans=0;
        sum.add(0);
        int n=fruits.length;
        for(int i=1;i<=n;++i){
            sum.add(sum.get(i-1)+fruits[i-1][1]);
        }
        int []pos=new int[n];
        for(int i=0;i<n;++i){
            pos[i]=fruits[i][0];
        }
        for(int red=k;red>=0;--red){
            // 折返距离因此需要除以2
            int dis=(k-red)/2;
            int l,r,lw,rw;
            // 先向左移动
            l=startPos-dis;
            r=startPos+red;
            lw=sum.get(lowerBound(pos,0,n,l));
            rw=sum.get(upperBound(pos,0,n,r));
            ans=Math.max(ans,rw-lw);

            // 先向右移动
            r=startPos+dis;
            l=startPos-red;
            lw=sum.get(lowerBound(pos,0,n,l));
            rw=sum.get(upperBound(pos,0,n,r));
            ans=Math.max(ans,rw-lw);
        }
        return ans;
    }
}