第十三届蓝桥杯大赛软件赛省赛（C/C++ 大学B组）

---

  虽然我的 $\mathrm{J}\mathrm{a}\mathrm{v}\mathrm{a}$ 组的，但怕被查重，等成绩公布了再做 $\mathrm{J}\mathrm{a}\mathrm{v}\mathrm{a}$ 的题解吧。

---

试题 A: 九进制转十进制

本题总分：$5$ 分

---

【问题描述】

  九进制正整数 $(2022{)}_9$ 转换成十进制等于多少？

【答案提交】

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

1478

---

#include 

int main() {
    int c, ans = 0;
    while (c = getchar(), '0' <= c && c <= '9')
        ans = ans * 9 + c - '0';
    printf("%d", ans);
}

  凭什么都是双非，$\mathrm{C}$ 的签到难度这么低。

  不公平不公平，重赛！重赛！

---

试题 B: 顺子日期

本题总分：$5$ 分

---

【问题描述】

  小明特别喜欢顺子。顺子指的就是连续的三个数字$：123、456$ 等。顺子日期指的就是在日期的 $\mathrm{y}\mathrm{y}\mathrm{y}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{d}\mathrm{d}$ 表示法中，存在任意连续的三位数是一个顺子的日期。例如 $20220123$ 就是一个顺子日期，因为它出现了一个顺子：$123$；而 $20221023$ 则不是一个顺子日期，它一个顺子也没有。小明想知道在整个 $2022$ 年份中，一共有多少个顺子日期。

---

【答案提交】

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

14

---

#include 

int year = 20220000, date, ans;

int days[13] = { 0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 }, buff[8];

int main() {
    for (int month = 1; month <= 12; ++month)
        for (int day = 1; day <= days[month]; ++day) {
            date = year + 100 * month + day;
            for (int i = 0; i < 8; ++i)
                buff[i] = date % 10, date /= 10;
            for (int i = 1; i < 7; ++i)
                if (buff[i] - buff[i + 1] == 1 &&
                    buff[i - 1] - buff[i] == 1) {
                    ++ans;
                    break;
                }
        }
    printf("%d", ans);
}

  虽然从题目描述中，无法直观的感受到所谓的顺子，是否包括如 $321$ 这样递减的连续自然数列，但描述给出的样例 $20221023$ 中包含了 $210$，基本上可以认为答案中不包含递减的连续自然数列的统计，但同时还有另一个问题，那就是顺子中能否包含 $0$。

  总之，我认为是能包含 $0$ 的，不愧是蓝桥，

  题面做的真是有够失败的呢。

---

试题 C: 刷题统计

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$10$ 分

---

【问题描述】

  小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 $a$ 道题目，周六和周日每天做 $b$ 道题目。请你帮小明计算，按照计划他将在第几天实现做题数大于等于 $n$ 题？

【输入格式】

  输入一行包含三个整数 $a,b$ 和 $n$。

【输出格式】

  输出一个整数代表天数。

【样例输入】

10 20 99

【样例输出】

8

【评测用例规模与约定】

  对于 $50\%$ 的评测用例，$1\le a,b,n\le 10^6$。
  对于 $100\%$ 的评测用例，$1\le a,b,n\le 10^{18}$。

---

#include 

long long a, b, n, ans;

int main() {
    scanf("%lld %lld %lld", &a, &b, &n);
    ans = n / (5 * a + 2 * b) * 7;
    n %= 5 * a + 2 * b;
    if (n > 5 * a)
        ans += 5 + ((n - 5 * a) + b - 1) / b;
    else
        ans += (n + a - 1) / a;
    printf("%lld", ans);
}

  没啥好说的，

  一个 $a/b$ 向上取整的小技巧就是 $(a+b-1)/b$ 向下取整。

---

试题 D: 修剪灌木

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$10$ 分

---

【问题描述】

  爱丽丝要完成一项修剪灌木的工作。

  有 $N$ 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晚会修剪一棵灌木，让灌木的高度变为 $0$ 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始，每天向右修剪一棵灌木。当修剪了最右侧的灌木后，她会调转方向，下一天开始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。

  灌木每天从早上到傍晚会长高 1 厘米，而其余时间不会长高。在第一天的早晨，所有灌木的高度都是 $0$ 厘米。爱丽丝想知道每棵灌木最高长到多高。

【输入格式】

  一个正整数 $N$ ，含义如题面所述。

【输出格式】

  输出 $N$ 行，每行一个整数，第行表示从左到右第 $i$ 棵树最高能长到多高。

【样例输入】

3

【样例输出】

4
2
4

【评测用例规模与约定】

  对于 $30\%$ 的数据，$N\le 10$。
  对于 $100\%$ 的数据，$1<N\le 10000$。

---

#include 

int n;

int max(int a, int b) { return a > b ? a : b; }

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        printf("%d ", 2 * max(i - 1, n - i));
}

  一颗灌木可以长到的最高高度，可能为：

  1. 在它第一次被修剪之前
  2. 它在某一次被修剪后，在此被修剪之前。

  对于第二种情况，很容易分类出第 $i$ 个灌木 $t_i$ 的最高高度为 $\max \{2\times (i-1),2\times (n-i)\}$，即对应着爱丽丝从左端点折返和爱丽丝从右端点折返 $t_i$ 能达到的最高高度的取值。

  同时 $2\times (i-1)\le i$，仅在 $i\le 1$ 成立，故对于第一种情况，无需额外的判断，直接取第二种情况的最大值即可。

---

试题 E: X 进制减法

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$15$ 分

---

【问题描述】

  进制规定了数字在数位上逢几进一。

  $X$ 进制是一种很神奇的进制，因为其每一数位的进制并不固定！例如说某种 $X$ 进制数，最低数位为二进制，第二数位为十进制，第三数位为八进制，则 $X$ 进制数 $321$ 转换为十进制数为 $65$。

  现在有两个 $X$ 进制表示的整数 $A$ 和 $B$，但是其具体每一数位的进制还不确定，只知道 $A$ 和 $B$ 是同一进制规则，且每一数位最高为 $N$ 进制，最低为二进制。请你算出 $A-B$ 的结果最小可能是多少。

  请注意，你需要保证 $A$ 和 $B$ 在 $X$ 进制下都是合法的，即每一数位上的数字要小于其进制。

【输入格式】

  第一行一个正整数 $N$，含义如题面所述。

  第二行一个正整数 $M_a$，表示 $X$ 进制数 $A$ 的位数。

  第三行 $M_a$ 个用空格分开的整数，表示 $X$ 进制数 $A$ 按从高位到低位顺序各个数位上的数字在十进制下的表示。

  第四行一个正整数 $M_b$，表示 $X$ 进制数 $B$ 的位数。

  第五行 $M_b$ 个用空格分开的整数，表示 $X$ 进制数 $B$ 按从高位到低位顺序各个数位上的数字在十进制下的表示。

  请注意，输入中的所有数字都是十进制的。

【输出格式】

  输出一行一个整数，表示 $X$ 进制数 $A-B$ 的结果的最小可能值转换为十进制后再模 $1000000007$ 的结果。

【样例输入】

11
3
10 4 0
3
1 2 0

【样例输出】

94

【样例说明】
  当进制为：最低位 $2$ 进制，第二数位 $5$ 进制，第三数位 $11$ 进制时，减法得到的差最小。此时 $A$ 在十进制下是 $108$，$B$ 在十进制下是 $14$，差值是 $94$。

【评测用例规模与约定】

  对于 $30\%$ 的数据，$N\le 10;M_a,M_b\le 8$。
  对于 $100\%$ 的数据，$2\le N\le 1000;1\le M_a,M_b\le 100000;A\ge B$。

---

#include 

typedef long long ll;

int n, m, ma, mb, ans, p = 1000000007;

int A[100010], B[100010], S[100010] = {1};

int max(int a, int b) { return a > b ? a : b; }

int main() {
    scanf("%d", &n);
    scanf("%d", &ma);
    for (int i = ma; i > 0; --i) scanf("%d", &A[i]);
    scanf("%d", &mb);
    for (int i = mb; i > 0; --i) scanf("%d", &B[i]);
    m = max(ma, mb);
    for (int i = 1; i <= m; ++i) {
        S[i] = (ll)(max(1, max(A[i], B[i])) + 1) * S[i - 1];
        ans = (ans + (ll)S[i - 1] * (A[i] - B[i]) % p + p) % p;
    }
    printf("%d", ans);
}

  稍微转变一下就是，设 $m=\max \{m_a,m_b\}$，找到一个序列 $S=\{s_i|s_i\le N|s_i>A_i,B_i,1\}$，$s_0=1$，$|S|=m$，使得 ${\sum }_{i=1}^m[{\prod }_{j=0}^{i-1}{s}_j(A_i-B_i)]$ 最小，

  对于任意合法 $n$、$X$，${\prod }_{i=0}^n{s}_i>{\sum }_{i=1}^{n-1}(x_i{\prod }_{j=0}^{i-1}{s}_j)$ 都成立，因为 ${\prod }_{i=0}^n{s}_i=1+{\sum }_{i=1}^{n-1}[(s_i-1){\prod }_{j=0}^{i-1}{s}_j]$。

  因为 $A\ge B$，所以必然存在一个最小的 $i$，使得所有 $i^{\prime }>i$ 都有 $A_{i^{\prime }}=B_{i^{\prime }}$ 且 $A_i\ge B_i$，我们的任务就是构造 $S$ 使得 $(A_i-B_i){\prod }_{j=0}^{i-1}{s}_j$ 最小。

  因此每个 $s_i$ 取最小值即可。

---

试题 F: 统计子矩阵

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$15$ 分

---

【问题描述】

  给定一个 $N\times M$ 的矩阵 $A$，请你统计有多少个子矩阵 (最小 $1\times 1$，最大 $N\times M$) 满足子矩阵中所有数的和不超过给定的整数 $K?$

【输入格式】

  第一行包含三个整数 $N,M$ 和 $K$。

  之后 $N$ 行每行包含 $M$ 个整数，代表矩阵 $A$。

【输出格式】

  一个整数代表答案。

【样例输入】

3 4 10
1 2 3 4
5 6 7 8
9 10 11 12

【样例输出】

19

【样例说明】
  满足条件的子矩阵一共有 $19$，包含：
  大小为 $1\times 1$ 的有 $10$ 个。
  大小为 $1\times 2$ 的有 $3$ 个。
  大小为 $1\times 3$ 的有 $2$ 个。
  大小为 $1\times 4$ 的有 $1$ 个。
  大小为 $2\times 1$ 的有 $3$ 个。

【评测用例规模与约定】

  对于 $30\%$ 的数据，$N,M\le 20$。
  对于 $70\%$ 的数据，$N,M\le 100$。
  对于 $100\%$ 的数据，$1\le N,M\le 500;0\le A_{ij}\le 1000;1\le K\le 250000000$。

---

  $O(m{n}^2\log m)$ 好像差点意思，放一放。

---

试题 G: 积木画

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$20$ 分

---

【问题描述】

  小明最近迷上了积木画，有这么两种类型的积木，分别为 $I$ 型（大小为 $2$ 个单位面积）和 $L$ 型（大小为 $3$ 个单位面积）$：$

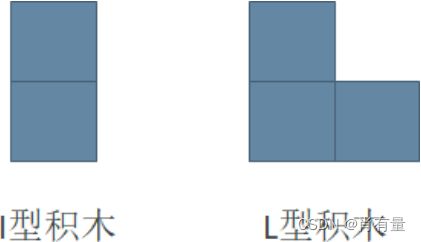
  同时，小明有一块面积大小为 $2\times N$ 的画布，画布由 $2\times N$ 个 $1\times 1$ 区域构成。小明需要用以上两种积木将画布拼满，他想知道总共有多少种不同的方式？积木可以任意旋转，且画布的方向固定。

【输入格式】

  输入一个整数 $N$，表示画布大小。

【输出格式】

  输出一个整数表示答案。由于答案可能很大，所以输出其对 $1000000007$ 取模后的值。

【样例输入】

3

【样例输出】

5

【样例说明】
  五种情况如下图所示，颜色只是为了标识不同的积木$：$

【评测用例规模与约定】

  对于所有测试用例，$1\le N\le 10000000$。

---

状压 DP

---

  按列划分后，第 $i$ 列能摆放某个积木是否合法，摆放后的方案数为几何，显然与第 $i-1$ 列有关，于是想到状压 $DP$。

  设 $f_{i,(00{)}_2}$、$f_{i,(01{)}_2}$、$f_{i,(10{)}_2}$、$f_{i,(11{)}_2}$，分别为 没有、第 $1$ 行 $i$ 列、$2$ 行 $i$ 列、$1$ 行 $i$ 列 和 $2$ 行 $i$ 列被某个积木占据的方法数。

  对于在 $i$ 列上的 $I$ 型积木的直立摆放，我们从 $f_{i-1,3}$ 上转移，躺平摆放则分别从 $f_{i-1,1}⟶f_{i,2}$、$f_{i-1,2}⟶f_{i,1}$，最后两个躺着的 $I$ 型积木 $f_{i-1,0}⟶f_{i,3}$。

  对于在 $i$ 列上的 $L$ 型积木的摆放，我们假定 $L$ 的朝向为上，此时它需要从 $f_{i-1,0}⟶f_{i,2}$，对于它朝向在 右、下、左 时则分别要从 $f_{i-1,0}⟶f_{i,1}$、$f_{i-1,2}⟶f_{i,3}$、$f_{i-1,1}⟶f_{i,3}$。

  于是有状态转移方程：$$\begin{array}{rl}{f}_{i,0}& =f_{i-1,3}\\ f_{i,1}& =f_{i-1,0}+f_{i-1,2}\\ f_{i,2}& =f_{i-1,0}+f_{i-1,1}\\ f_{i,3}& =f_{i-1,0}+f_{i-1,1}+f_{i-1,2}+f_{i-1,3}\end{array}$$  但其实根本不需要这么多状态，因为 $f_{i,0}$ 可以直接由 $f_{i-1,3}$ 确定，而将状态 $(01{)}_2$ 的摆放法垂直翻转后就能得到状态为 $(10{)}_2$ 的方案数，由此我们可以得出结论对于任意 $i$ 都有 $f_{i,1}=f_{i,2}$，依此为基础进一步优化状态转移方程：

  $\begin{array}{rl}{f}_{i,1}& =f_{i-2,3}+f_{i-1,1}\\ & =f_{i-2,3}+f_{i-3,3}+f_{i-2,1}\\ & =f_{i-2,3}+f_{i-3,3}+\cdots +f_{0,3}+f_{1,1}\\ & =\sum _{j=0}^{i-2}{f}_{j,3}\end{array}$

  将 $f_{i,3}$ 变化符号为 $f_i$，又 $f_{1,1}$ 显然等于 $0$，故有：

  $f_{i,1}={\sum }_{j=0}^{i-2}{f}_j$

  $f_i={\sum }_{j=0}^{i-1}{f}_j+{\sum }_{j=0}^{i-3}{f}_j$

  $\begin{array}{rl}{f}_i-f_{i-1}& =\sum _{j=0}^{i-1}{f}_j-\sum _{j=0}^{i-2}{f}_j+\sum _{j=0}^{i-3}{f}_j-\sum _{j=0}^{i-4}{f}_j\\ & =f_{i-1}+f_{i-3}\end{array}$
  最终$$f_i=2f_{i-1}+f_{i-3}$$  初始时 $f_0=1$，$f_1=1$，$f_2=2$，答案为 $f_n$。

  草，不该推这个式子的，

  浪费时间。

#include 

int n, p = 1000000007, dp[10000010] = {1, 1, 2};

int main() {
    scanf("%d", &n);
    for (int i = 3; i <= n; ++i)
        dp[i] = (2 * dp[i - 1] + dp[i - 3]) % p;
    printf("%d", dp[n]);
}

---

试题 H: 扫雷

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$20$ 分

---

【问题描述】

  小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下，在一个二维平面上放置着 $n$ 个炸雷，第 $i$ 个炸雷 $(x_i,y_i,r_i)$ 表示在坐标 $(x_i,y_i)$ 处存在一个炸雷，它的爆炸范围是以半径为 $r_i$ 的一个圆。

  为了顺利通过这片土地，需要玩家进行排雷。玩家可以发射 $m$ 个排雷火箭，小明已经规划好了每个排雷火箭的发射方向，第 $j$ 个排雷火箭 $(x_j,y_j,r_j)$ 表示这个排雷火箭将会在 $(x_j,y_j)$ 处爆炸，它的爆炸范围是以半径为 $r_j$ 的一个圆，在其爆炸范围内的炸雷会被引爆。同时，当炸雷被引爆时，在其爆炸范围内的炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷？

  你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。

【输入格式】

  输入的第一行包含两个整数 $n、m$。

  接下来的 $n$ 行，每行三个整数 $x_i,y_i,r_i$，表示一个炸雷的信息。

  再接下来的 $m$ 行，每行三个整数 $x_j,y_j,r_j$，表示一个排雷火箭的信息。

【输出格式】

  输出一个整数表示答案。

【样例输入】

2 1
2 2 4
4 4 2
0 0 

【样例输出】

2

【样例说明】
  示例图如下，排雷火箭 $1$ 覆盖了炸雷 $1$，所以炸雷 $1$ 被排除；炸雷 $1$ 又覆盖了炸雷 $2$，所以炸雷 $2$ 也被排除。

【评测用例规模与约定】

  对于 $40\%$ 的评测用例$：0\le x,y\le 10^9,0\le n,m\le 10^3,1\le r\le 10$。
  对于 $100\%$ 的评测用例$：0\le x,y\le 10^9,0\le n,m\le 5\times 10^4,1\le r\le 10$。

---

// 涉及到几何的就不想写，摆了。

---

试题  I: 李白打酒加强版

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$25$ 分

---

【问题描述】

  话说大诗人李白，一生好饮。幸好他从不开车。

  一天，他提着酒壶，从家里出来，酒壶中有酒 $2$ 斗。他边走边唱$：$

  无事街上走，提壶去打酒。
  逢店加一倍，遇花喝一斗。

  这一路上，他一共遇到店 $N$ 次，遇到花 $M$ 次。已知最后一次遇到的是花，他正好把酒喝光了。

  请你计算李白这一路遇到店和花的顺序，有多少种不同的可能？

  注意：壶里没酒 ( $0$ 斗) 时遇店是合法的，加倍后还是没酒；但是没酒时遇花是不合法的。

【输入格式】

  第一行包含两个整数 $N$ 和 $M$。

【输出格式】

  输出一个整数表示答案。由于答案可能很大，输出模 $1000000007$ 的结果。

【样例输入】

5 10

【样例输出】

14

【样例说明】
  如果我们用 0 代表遇到花，1 代表遇到店，14 种顺序如下$：$
$$\begin{gathered} 010101101000000 \\ 010110010010000 \\ 011000110010000 \\ 100010110010000 \\ 011001000110000 \\ 100011000110000 \\ 100100010110000 \\ 010110100000100 \\ 011001001000100 \\ 100011001000100 \\ 100100011000100 \\ 011010000010100 \\ 100100100010100 \\ 101000001010100 \end{gathered}$$

【评测用例规模与约定】

  对于 $40\%$ 的评测用例$：1\le N,M\le 10$。
  对于 $100\%$ 的评测用例$：1\le N,M\le 100$。

---

动态规划

---

  当壶中酒的斗数大于 $m$ 时，无论如何都无法使酒喝光，于是限制其上限为 $m$，考虑动态规划。

  设 $f_{i,j,k}$ 为李白在经过 $i$ 家店和遇 $j$ 次花后使得酒还剩 $k$ 斗的方案数。

  若李白此刻遇花，则有 $f_{i,j,k}=f_{i,j-1,k+1}$。

  若李白此刻进店，则考虑 $k$ 是否为 $2$ 的倍数，若是将 $f_{i,j,k}$ 累加上一个 $f_{i-1,j,\frac{k}{2}}$。

  最后特判一下很麻烦，索性就输出 $f_{n,m-1,1}$ 了。

  关于提醒无酒进店是合法的其实我没看太懂，因为最后一刻要求遇花且恰把酒喝完，而出现无酒后无论如何都无法达到一个剩余一定的酒且遇花合法的状态，关键这作为压轴题也太简单的离谱了。

  蓝桥，看不透。

#include 

int n, m, p = 1000000007, dp[101][101][101]= { 0, 0, 1};

int main() {
    scanf("%d %d", &n, &m);
    for (int i = 0; i <= n; ++i)
        for (int j = 0; j < m; ++j)
            for (int k = 1; k <= m; ++k) {
                if (i && k % 2 == 0) dp[i][j][k] = dp[i - 1][j][k / 2];
                if (j) dp[i][j][k] = (dp[i][j][k] + dp[i][j - 1][k + 1]) % p;
            }
    printf("%d", dp[n][m - 1][1]);
}

---

试题 J: 砍竹子

时间限制: $1.0\mathrm{s}$ 内存限制: $256.0\mathrm{M}\mathrm{B}$ 本题总分：$25$ 分

---

【问题描述】

  这天，小明在砍竹子，他面前有 $n$ 棵竹子排成一排，一开始第 i 棵竹子的高度为 $h_i$。

  他觉得一棵一棵砍太慢了，决定使用魔法来砍竹子。魔法可以对连续的一段相同高度的竹子使用，假设这一段竹子的高度为 $H$，那么使用一次魔法可以把这一段竹子的高度都变为 $\lfloor \sqrt{\lfloor \frac{H}{2}\rfloor +1}\rfloor$，其中 $\lfloor x\rfloor$ 表示对 $x$ 向下取整。小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为 $1$。

【输入格式】

  第一行为一个正整数 $n$，表示竹子的棵数。

  第二行共 $n$ 个空格分开的正整数 $h_i$，表示每棵竹子的高度。

【输出格式】

  一个整数表示答案。

【样例输入】

6
2 1 4 2 6 7

【样例输出】

5

【样例说明】
  其中一种方案$：$
  $214267$
  $\to 214262$
  $\to 214222$
  $\to 211222$
  $\to 111222$
  $\to 111111$
  共需要 $5$ 步完成

【评测用例规模与约定】

  对于 $20\%$ 的数据，保证 $n\le 1000,h_i\le 10^6$。
  对于 $100\%$ 的数据，保证 $n\le 2\times 10^5,hi\le 10^{18}$。

---

  想起那年国赛，压轴题 $O(n\log n)$ 的贪心排序，$n\le 1e3$，时间限制给了 $3$ 秒。

  就很会你知道吧。

---

贪心

---

  如果一排最大连续的竹子高度相同且高度不为 $1$，那么在一个可行的最优解中，一定存在有若干次魔法包含这一排竹子，简单证明一下：

  设这排竹子在 $[i,j]$ 上最大连续，若有一次魔法不是将它们全部包含，设魔法的操作区间为 $[x,y]$，因为 $[i,j]$ 的最大性，$[x,y]$ 一定被它们包含，若 $[x,y]$ 没有落在端点上，则这次魔法对 $[1,i)$、$(j,n]$ 没有贡献一定不优，否则对将来出现的包含 $[x,y]$ 的操作 $[k,g]$ 全部转为 $[k,i)$，现在的 $[x,y]$ 跟随 $[i,j]$ 一起变化，答案一定不会变少。

  并且一个高度只受变化公式的影响而与魔法顺序无关。

  容易想到贪心策略，即：

  建立一个优先队列将连续的一排竹子加入进去。

  每次取出最高的竹子，并检查列队剩余的竹子是否能加入到这一排中，然后对其释放魔法，最后回到该步开头直至队列为空。

  写的真粪

#include 
#include 
#include 

struct Node {

    int l, r;

    long long h;

    Node(int l1, int r1, long long h1) : l(l1), r(r1), h(h1) {}

    inline bool operator<(const Node &n) const { return h == n.h ? l > n.l : h < n.h; }
};

std::priority_queue<Node> q;

int n, h, ans;

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &h), q.push(Node(i, i, h));
    while (q.size()) {
        if (q.top().h == 1) break;
        Node now = q.top();
        q.pop();
        while (q.size() && q.top().h == now.h && q.top().l == now.r + 1)
            now.r = q.top().r, q.pop();
        ++ans;
        now.h = sqrt(now.h / 2 + 1);
        if (now.h > 1) q.push(now);
    }
    printf("%d", ans);
}

  想考他人贪心算法的都是**。