元学习之《On First-Order Meta-Learning Algorithms》论文详细解读
元学习系列文章
- optimization based meta-learning
- 《Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks》 论文翻译笔记
- 元学习方向 optimization based meta learning 之 MAML论文详细解读
- MAML 源代码解释说明 (一)
- MAML 源代码解释说明 (二)
- 元学习之《On First-Order Meta-Learning Algorithms》论文详细解读:本篇博客
- 元学习之《OPTIMIZATION AS A MODEL FOR FEW-SHOT LEARNING》论文详细解读
- metric based meta-learning: 待更新…
- model based meta-learning: 待更新…
文章目录
-
-
- 引言
- On First-Order Meta-Learning Algorithms
-
- 伪算法
- 数学过程
- 训练过程
- 实验
- 核心代码
- OpenAI Demo
- 几点思考
- 参考资料
-
引言
上一篇博客对论文 MAML 做了详细解读,MAML 是元学习方向 optimization based 的开篇之作,还有一篇和 MAML 很像的论文 On First-Order Meta-Learning Algorithms,该论文是大名鼎鼎的 OpenAI 的杰作,OpenAI 对 MAML 做了简化,但效果却优于 MAML,具体做了什么简化操作,请往下看。
On First-Order Meta-Learning Algorithms
这篇论文的标题就很针对 MAML,MAML 中有一个重要的特点,就是在求梯度时,为了加速放弃了二阶求导,使用一阶微分近似进行代替,虽然效果上相差不大,但总感觉少了点什么。这篇论文的标题上来就声称我们是一阶的 metalearning 方法,而且刚好是在 MAML 发表的下一年(2018)发表在 ICML 会议的,从标题上也是赚慢了噱头。
还有个有意思的事情,OpenAI 把论文中的算法称之为 Reptile, 但是也没有解释为什么叫这个,论文中也没看出来和 Reptile 有什么关联,感兴趣的读者,可以去深究一下。
说了一堆废话,下面开始进入正题。
伪算法
1 首先初始化一个网络模型的所有参数 ϕ \phi ϕ
2 迭代 N 次,进行训练,每次迭代执行:
- 2.1 随机抽样一个任务 T,用网络模型进行训练,对应的loss 是 L t L_t Lt,训练结束后的参数是 ϕ ~ \widetilde{\phi} ϕ
- 2.2,在参数 ϕ \phi ϕ上使用 SGD 或 Adam 执行K次梯度下降更新,得到 ϕ ~ = U t k ( ϕ ) \widetilde{\phi}={U}^{k}_{t}(\phi) ϕ =Utk(ϕ)
- 2.3 用 ϕ ~ \widetilde{\phi} ϕ 更新网络模型模型参数, ϕ = ϕ + ϵ ( ϕ ~ − ϕ ) \phi=\phi+\epsilon(\widetilde{\phi}-\phi) ϕ=ϕ+ϵ(ϕ −ϕ)
3 完成上述N次迭代训练,则结束整个过程
从上面的算法中可以看出,Reptile 是在每个单独的任务执行K次训练后,就开始真正更新网络模型的参数(Meta),更新方式不是梯度下降,但是和梯度下降公式长得很像,是用上一次的参数 ϕ \phi ϕ和K次后的参数 ϕ ~ \widetilde{\phi} ϕ 的差来更新,更新的步长是 ϵ \epsilon ϵ。在这个过程中,只有一阶求导的计算,就是在任务内部执行K次更新的过程中用到的随机梯度下降,这也是为什么标题中叫 First-Order 的原因。
从这就可以看出和 MAML 算法的不同了:
- MAML:所有任务执行完,用每个任务测试集上的平均 loss 来更新 meta 参数。
- Reptile:每个任务执行K次训练后,用最新的参数和 meta 参数的差来更新 meta 参数。
这里说的meta参数,就是真正更新网络模型参数的过程
数学过程
上面只是简单介绍了 Reptile 的算法思想,下面从数学过程上来理解下它的更新过程,先来设定几个符号:
ϕ \phi ϕ代表网络模型初始参数, ϵ , η \epsilon,\eta ϵ,η分别代表 meta 更新的学习率和 task 更新的学习率, N N N是meta训练的 batch_size,即 meta 的一个bach有 N 个task,每个task内部执行K次训练,N个任务都训练完,再来更新meta参数。按照上面的算法过程,meta的一个batch训练完之后,网络模型的参数是:
ϕ = ϕ + ϵ 1 N ∑ i = 1 N ( ϕ i ~ − ϕ ) = ϕ + ϵ ( W − ϕ ) \begin{aligned} \phi &= \phi +\epsilon \frac{1}{N}\sum_{i=1}^{N}\left ( \tilde{\phi_i } -\phi\right )\\ &= \phi +\epsilon \left ( W-\phi \right )\\ \end{aligned} ϕ=ϕ+ϵN1i=1∑N(ϕi~−ϕ)=ϕ+ϵ(W−ϕ)
其中 W W W是每个任务最后参数的平均值,上述公式再进行展开就是这样:
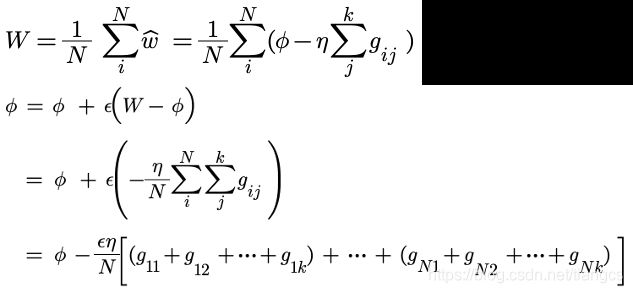
假设N=2,K=3,即meta每次训练的一个batch 有2个task,每个task内部进行3此迭代,则 meta每次更新模型参数的公式为:
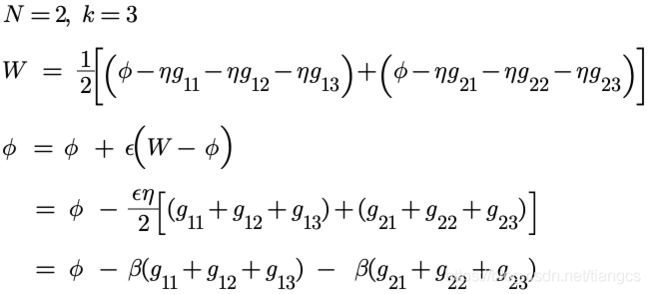
训练过程
上面公式的最后一行,又变成了熟悉的梯度下降,只不过梯度方向是每个任务内部更新的几次梯度方向的和。meta 模型的参数更新过程,在几何上就是这样的:
![]()
动图看的更加清晰些,其中绿色代表第一个任务,三个绿色箭头代表三次更新时的梯度方向,可以看到,Reptile的模型就是朝着每个任务的梯度和的方向上不断地进行更新。
还记得 MAML 是怎样更新的吗?不记得的话,请翻看上一篇博客。还是同样的设置,MAML 的更新过程如下:
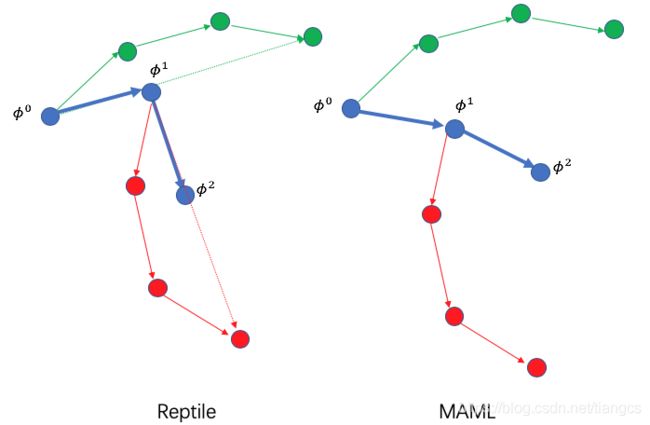
即 MAML 是在每个任务最后一个梯度的方向上进行更新,而 Reptile 是在每个任务几个梯度和的方向上进行更新。
实验
实验设置和 MAML 论文中的设置一样,回归任务以拟合正弦函数为例,分类任务以 MiniImagenet 数据和 omniglot 数据的图片分类为例,详细设置就不再赘述了,直接看实验结果:
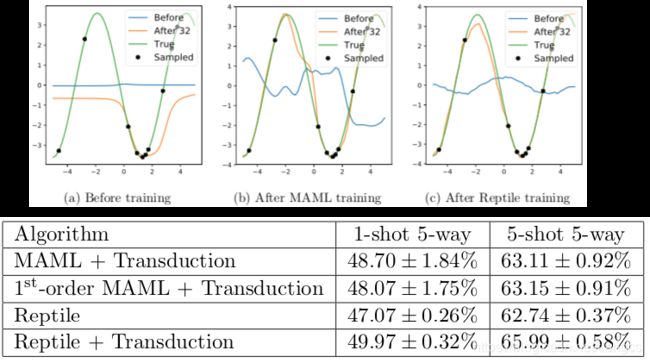
上半部分的图是正弦函数的拟合结果,(b)是MAML的结果,C是Reptile的结果,橘黄色线是微调32次之后的样子,绿色线是真实分布,可以看到 Reptile和MAML的结果相当,都能拟合到真实分布的样子,硬要一较高下的话,那就是 Reptile稍好一些。
下半部分图是在 MiniImagenet 分类数据上的结果,作者也对比了一阶近似 MAML和二阶MAML的结果,从图中可以看出,Reptile的准确率至少要高出1个百分点。
在论文中作者还对比了一个有意思的实验,Reptile 既然可以在 g 1 + g 2 + g 3 g_1+g_2+g_3 g1+g2+g3 的梯度方向上更新,那么如果在其它梯度的组合方向上去更新,结果会怎样呢?比如 g 1 + g 2 g_1+g_2 g1+g2 等方向,作者也针对不同梯度的组合进行了实验,实验结果如下:
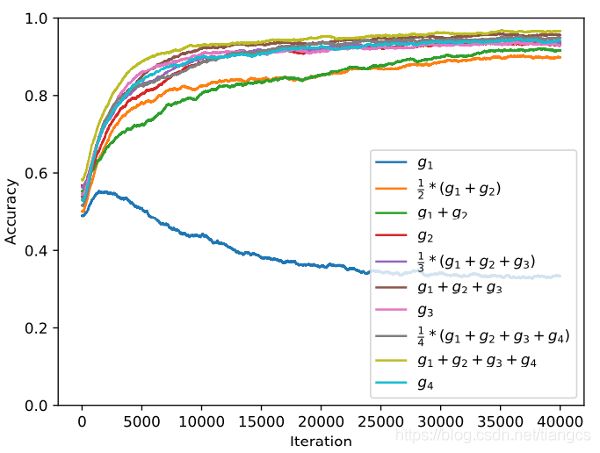
横轴是meta迭代次数,纵轴是准确率,不同颜色的曲线代表不同的梯度组合,可以明显的看到最下面的蓝色曲线准确率最低,蓝色曲线代表在 g 1 g_1 g1 第一个梯度方向上去更新,其实就是模型预训练的过程,以所有训练任务的 loss 为准进行更新。其他颜色的曲线都代表用若干次之后的 loss 来更新参数,最上面的那条曲线代表 Reptile,即用 g 1 + g 2 + g 3 + g 4 g_1+g_2+g_3+g_4 g1+g2+g3+g4 的梯度方向进行更新,只使用 g 4 g_4 g4 的那条曲线代表 MAML。
核心代码
Reptile 的论文代码也是开源的,而且代码很简介规范,不愧是 OpenAI 出品。建议感兴趣的读者去看下论文源码,不仅能更好的理解论文思想,对工程能力的提升也很有帮助,包括代码风格、模块化、组织架构、逻辑实现等都有很多值得借鉴的地方。关于源代码有疑问的话,可以私信联系我。这里只贴一点核心的训练更新代码,对应上面的数学过程:
代码文件见 reptile.py
# 取出网络模型的最新参数
old_vars = self._model_state.export_variables()
# 保存一个 meta batch 里,每个 task 更新 K 次后的参数
new_vars = []
for _ in range(meta_batch_size):
# 抽样出一个 task
mini_dataset = _sample_mini_dataset(dataset, num_classes, num_shots)
for batch in _mini_batches(mini_dataset, inner_batch_size, inner_iters, replacement):
# task 里面的训练,更新 inner_iters 次,相当于公式中的K
inputs, labels = zip(*batch) # inner_iters 个 batch,每个 iter 使用一个 batch ,里面的一次训练迭代
if self._pre_step_op:
self.session.run(self._pre_step_op)
self.session.run(minimize_op, feed_dict={input_ph: inputs, label_ph: labels})
# 一个 task 内部训练完的参数
new_vars.append(self._model_state.export_variables())
self._model_state.import_variables(old_vars)
# 对 meta_batch 个 task 的最终参数进行平均,相当于公式中的 W
new_vars = average_vars(new_vars)
# 所有的 meta_batch 个任务都训练完, 更新一次 meta 参数,并且把更新后的参数更新到计算图中,下次训练从最新参数开始
# 更新方式:old + scale*(new - old)
self._model_state.import_variables(interpolate_vars(old_vars, new_vars, meta_step_size))
OpenAI Demo
在 OpenAI 的官方博客 Reptile: A Scalable Meta-Learning Algorithm中,也有介绍这篇论文。该博客网页中还有个有意思的 demo,大家可以试玩一下:

这个 demo 的意思是,openAI 已经用他们的 Reptile 算法训练了一个用于少样本场景的3分类网络模型,并且嵌入到了网页中,用户可以通过 demo 中的交互制作一个新的三分类任务,并且这个任务只有三个训练样本,也就是每个类下只有一个样本,学名叫3-Way 1-shot,让他们的模型在这三个样本上进行微调学习,然后在右边画一个新的三个类别下的测试样本,Reptile 模型会自动给出它在三个类别下的概率。通过这个 demo 来证明他们的模型确实有奇效,在新任务的几个样本上微调一下,就可以在该任务的测试集上取得很好的准确率。
几点思考
通过上面的 demo 可以得出一些结论:
- 画图框是固定尺寸,而且是黑白图案,相当于输入大小是固定的,所以可以用同一个模型进行训练
- 框里面可以任意画一些图案,比如画数字
1,2,3的图案,那就变成了少样本手写数字识别任务;画A,B,C的图案,那就变成了手写字母识别;画三个猫、狗、兔子的图案,那就变成了动物识别;这样是不是说明了,通过 meta-learning 的方法预训练网络模型,可以在视觉场景中有广泛应用 ?因为只要输入图片的尺寸是固定的,就可以一个模型应对所有任务。不知道这样想是不是对的,如果是的话,那感觉看到了一个巨大的商机。 - Reptile 的方法能不能用到传统的结构化数据上进行迁移 ?这就涉及到对 task 定义以及 task 间相似性的理解了,欢迎感兴趣的读者一起交流。
参考资料
- https://arxiv.org/pdf/1803.02999.pdf
- https://github.com/openai/supervised-reptile
- https://www.bilibili.com/video/BV1Gb411n7dE?p=32
