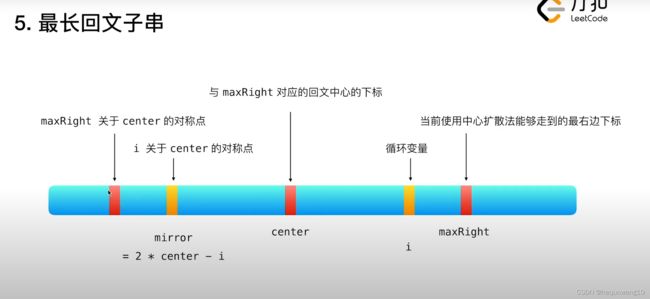
Manacher算法
Manacher算法(马拉车)
马拉车算法可以在O(n)的时间复杂度求解一个字符串的最长回文子串长度。
分析
初始化
第一步:初始化
情况1:i>=maxRight
p数组表示的是当前下标向两边扩散能够扩散的最多步数。
开始的时候i>=maxRight,p[0] = 0。

然后循环变量走至下一位,此时两边都是#好,所以最大的步数是1。
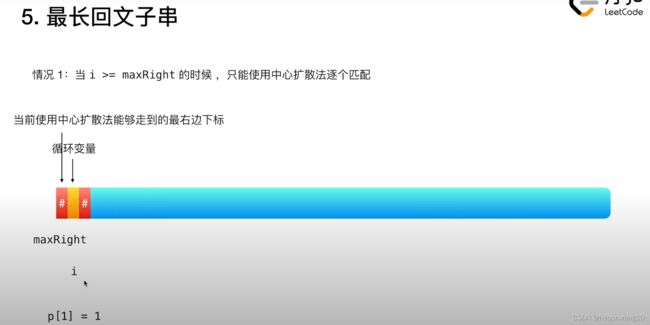
此时更新maxRight的值,此时maxRight的值是严格大于i的。这就是情况2了。
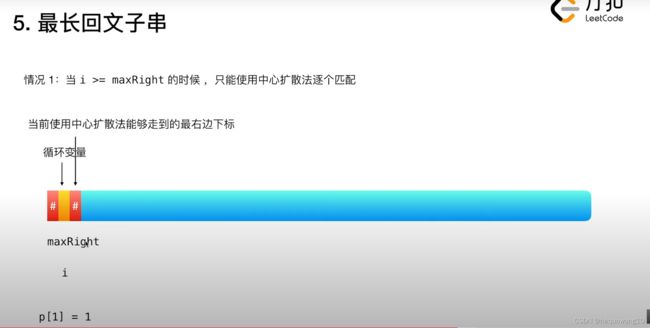
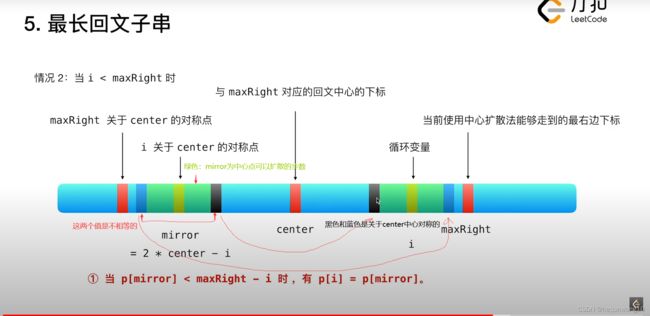
情况2:i
如下图所示,此时i的值,尽可能的参考i关于center对称的镜像mirror位置。
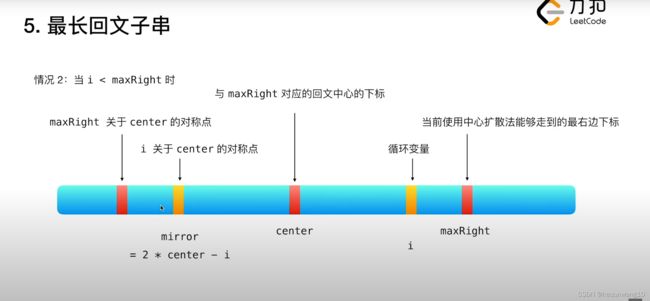
所以根据mirror的值大小可以分为三种情况:主要判断mirror的位置可以扩散的步数是否等于maxRight到i的位置。
第一种:p[mirror] < maxRight - i
因为mirror为中心向两边扩散的步数小于maxRight-i,所以以i为中心向两边扩散的步数等于mirror的步数。
p[i] = p[mirror]
第二种:p[mirror] = maxRight - i
此时mirror可以向两边扩散的步数正好走到了maxRight关于center的对称点,也就是p[mirror] = maxRight - i。

我们根据mirror的对称性和center点的对称性,我们可以发现关于i为中心可以扩散的情况主要是看maxRight的值与黑色的值是否相等。
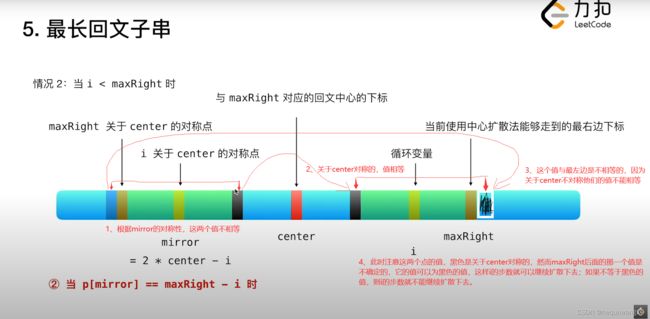
所以以i为中心的点向左右扩散的步数至少是maxRight - i的。
p[i] >= maxRight - i

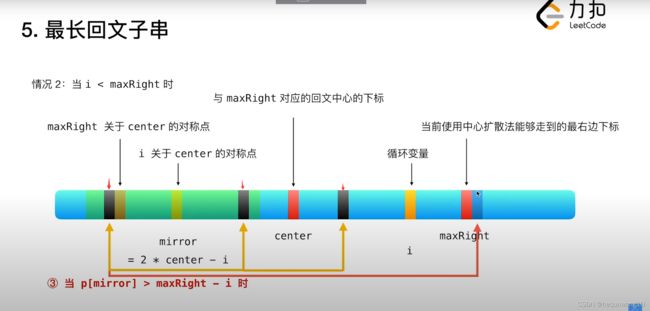
第三种:p[mirror] > maxRight - i
由mirror的对称性和center的对称性转移,发现黑色的值恰好传递为i的最左边位置,但是以center为中心的最长步数的两个点,黑色是不等于maxRight+1的位置的点的,所以以i为中心的最长步数等于maxRight - i。
总结
代码
647.回文子串
一、题目描述
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc"
输出:3
解释:三个回文子串: "a", "b", "c"
示例 2:
输入:s = "aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
二、解题
可以得到 S 所有点为中心的最大回文半径,也就能够得到 S 中所有可能的回文中心的的最大回文半径,把它们累加就可以得到答案。
class Solution {
public int countSubstrings(String s) {
int length = s.length();
if(length < 2){
return s.length();
}
String str = addDividers(s,'#');
int sLen = 2*length+1;
//p[i] :以预处理字符串下标i为中心的回文半径(奇数长度是不包括中心)
//p是首字符。
int[] p = new int[sLen];
//通过中心扩散的方式能扩散的最右边的下标
int maxRight = 0;
//与maxRight对应的中心字符的下标
int center = 0;
int maxLen = 1;
int begin = 0;
int res = 0;
char[] charArray = str.toCharArray();
for(int i = 0;i<sLen;i++){
if(i < maxRight){
//状态转移方程
int mirror = 2 * center - i;
p[i] = Math.min(maxRight - i,p[mirror]);
}
//尝试使用中心扩散法 更新p[i]的值
int left = i - (1+p[i]);
int right = i + (1+p[i]);
while(left>=0 && right<sLen && charArray[left] == charArray[right]){
p[i]++;
left--;
right++;
}
//更新maxRight,他是遍历过的i的i+p[i]的最大值
if(i+p[i] > maxRight){
//maxRight 和 center同时更新
maxRight = i + p[i];
center = i;
}
//统计答案,当前(p[i]+1)/2;
res += ((p[i]+1)/2) ;
//记录最长回文子串的长度和相应它在原始字符串的起点
if(p[i] > maxLen){
maxLen = p[i];
begin = (i - maxLen) / 2;
}
}
return res;
}
//预处理字符串
public String addDividers(String s,char divider){
if(s.indexOf(divider) != -1){
return null;
}
char[] charArray = s.toCharArray();
int length = s.length();
StringBuilder sb = new StringBuilder();
for(int i = 0;i<length;i++){
sb.append(divider);
sb.append(charArray[i]);
}
sb.append(divider);
return sb.toString();
}
}
注
如果返回最大长度的回文子字符串。
public String longSubstrings(String s) {
int length = s.length();
if(length < 2){
return s;
}
String str = addDividers(s,'#');
int sLen = 2*length+1;
//p[i] :以预处理字符串下标i为中心的回文半径(奇数长度是不包括中心)
//p是首字符。
int[] p = new int[sLen];
//通过中心扩散的方式能扩散的最右边的下标
int maxRight = 0;
//与maxRight对应的中心字符的下标
int center = 0;
int maxLen = 1;
int begin = 0;
int res = 0;
char[] charArray = str.toCharArray();
for(int i = 0;i<sLen;i++){
if(i < maxRight){
//状态转移方程
int mirror = 2 * center - i;
p[i] = Math.min(maxRight - i,p[mirror]);
}
//尝试使用中心扩散法 更新p[i]的值
int left = i - (1+p[i]);
int right = i + (1+p[i]);
while(left>=0 && right<sLen && charArray[left] == charArray[right]){
p[i]++;
left--;
right++;
}
//更新maxRight,他是遍历过的i的i+p[i]的最大值
if(i+p[i] > maxRight){
//maxRight 和 center同时更新
maxRight = i + p[i];
center = i;
}
//统计答案,当前(p[i]+1)/2;
res += ((p[i]+1)/2) ;
//记录最长回文子串的长度和相应它在原始字符串的起点
if(p[i] > maxLen){
maxLen = p[i];
begin = (i - maxLen) / 2;
}
}
return s.substring(begin,begin+maxLen);
}
完整代码
class Solution2 {
//计算最长的回文子串
public String longSubstrings(String s) {
int length = s.length();
if(length < 2){
return s;
}
String str = addDividers(s,'#');
int sLen = 2*length+1;
//p[i] :以预处理字符串下标i为中心的回文半径(奇数长度是不包括中心)
//p是首字符。
int[] p = new int[sLen];
//通过中心扩散的方式能扩散的最右边的下标
int maxRight = 0;
//与maxRight对应的中心字符的下标
int center = 0;
int maxLen = 1;
int begin = 0;
int res = 0;
char[] charArray = str.toCharArray();
for(int i = 0;i<sLen;i++){
if(i < maxRight){
//状态转移方程
int mirror = 2 * center - i;
p[i] = Math.min(maxRight - i,p[mirror]);
}
//尝试使用中心扩散法 更新p[i]的值
int left = i - (1+p[i]);
int right = i + (1+p[i]);
while(left>=0 && right<sLen && charArray[left] == charArray[right]){
p[i]++;
left--;
right++;
}
//更新maxRight,他是遍历过的i的i+p[i]的最大值
if(i+p[i] > maxRight){
//maxRight 和 center同时更新
maxRight = i + p[i];
center = i;
}
//统计答案,当前(p[i]-1)/2;
res += (p[i]/2) ;
//记录最长回文子串的长度和相应它在原始字符串的起点
if(p[i] > maxLen){
maxLen = p[i];
begin = (i - maxLen) / 2;
}
}
return s.substring(begin,begin+maxLen);
}
//统计数量
public int countSubstrings(String s) {
int length = s.length();
String str = addDividers(s,'#');
int sLen = 2*length+1;
//p[i] :以预处理字符串下标i为中心的回文半径(奇数长度是不包括中心)
//p是首字符。
int[] p = new int[sLen];
//通过中心扩散的方式能扩散的最右边的下标
int maxRight = 0;
//与maxRight对应的中心字符的下标
int center = 0;
int maxLen = 1;
int begin = 0;
int res = 0;
char[] charArray = str.toCharArray();
for(int i = 0;i<sLen;i++){
if(i < maxRight){
//状态转移方程
int mirror = 2 * center - i;
p[i] = Math.min(maxRight - i,p[mirror]);
}
//尝试使用中心扩散法 更新p[i]的值
int left = i - (1+p[i]);
int right = i + (1+p[i]);
while(left>=0 && right<sLen && charArray[left] == charArray[right]){
p[i]++;
left--;
right++;
}
//更新maxRight,他是遍历过的i的i+p[i]的最大值
if(i+p[i] > maxRight){
//maxRight 和 center同时更新
maxRight = i + p[i];
center = i;
}
//统计答案,当前(p[i]+1)/2;
res += ((p[i]+1)/2) ;
//记录最长回文子串的长度和相应它在原始字符串的起点
if(p[i] > maxLen){
maxLen = p[i];
begin = (i - maxLen) / 2;
}
}
return res;
}
//预处理字符串
public String addDividers(String s,char divider){
if(s.indexOf(divider) != -1){
return null;
}
char[] charArray = s.toCharArray();
int length = s.length();
StringBuilder sb = new StringBuilder();
for(int i = 0;i<length;i++){
sb.append(divider);
sb.append(charArray[i]);
}
sb.append(divider);
return sb.toString();
}
public static void main(String[] args){
Solution2 solu = new Solution2();
String s = "abaabacdeaabaab";
String longstr = solu.longSubstrings(s);
int res = solu.countSubstrings(s);
System.out.println(longstr);
System.out.println(res);
}
}