强化学习（九）- 策略梯度方法 - 梯度上升，黑箱优化，REINFORCE算法及CartPole实例

引言

在之前介绍的方法中，几乎所有方法都是动作价值方法（action-value Method），通过学习动作价值并基于动作价值来学做动作。如果没有动作价值评估，他们的策略甚至不会存在。但在这个部分我们将考虑学习参数化策略的方法，这些方法可以在不考虑价值函数的情况下选择动作。价值函数仍然可以用于学习策略参数，但对于动作选择是不必要的。我们使用$\theta \in {\mathbb{R}}^{d^{\prime }}$来表示策略的参数向量。所以使用$\pi (a|s,\theta )=Pr\{A_t=a|S_t=s,{\theta }_t=\theta \}$表示在$t$时刻$a$被采取的概率， 假设环境在$t$时刻处于带有参数的状态$s$。如果一个方法也使用了学习的价值函数，那么价值函数的权重向量照例表示为$\text{w}\in {\mathbb{R}}^{d^{\prime }}$，如$\hat{v}(s,\text{w})$。

在这个部分我们使用基于一些标量性能度量$J(\theta )$相对于策略参数的梯度来学习策略参数的方法。这些方法寻求性能最大化，因此它们的更新近似于$J$的梯度上升（gradient ascent）。

$${\theta }_{t+1}={\theta }_t+\alpha \nabla J({\theta }_t)\text{\hspace{1em}(9.1)}$$

其中$\nabla J({\theta }_t)\in {\mathbb{R}}^d$是一个随机估计，其期望值近似于性能度量相对于其参数${\theta }_t$的梯度。所有遵循这个一般模式的方法，我们都称之为策略梯度方法，不管它们是否也学习了一个近似的价值函数。同时学习策略和价值函数近似值的方法通常被称为执行者-评论者方法（actor–critic methods） ，其中行为者是指学习的策略，评论者指学习的价值函数，通常是状态价值函数。首先，我们处理偶发情况，在这种情况下，性能被定义为参数化策略下的起始状态值，然后再去考虑持续情况，在这种情况下，性能被定义为平均奖励率。最后，我们能够用非常相似的术语来表达这两种情况的算法。

我们考虑基于策略的方法有三个原因:

1. 简易性:基于策略的方法直接处理手头的问题(估计最优策略)，而不需要存储一堆可能没有用处的额外数据(即动作值)。
2. 随机策略:与基于价值的方法不同，基于策略的方法可以学习真正的随机策略。
3. 连续动作空间:基于策略的方法非常适合连续动作空间。

9.1 策略近似和其优势

在策略梯度方法中，策略可以以任何方式参数化，只要$\pi (a|s,\theta )$对其参数是可微的，也就是说，只要$\nabla \pi (a|s,\theta )$存在，并且对于所有$s\in \mathcal{S},a\in \mathcal{A},\theta \in {\mathbb{R}}^{d^{\prime }}$是有限的。在实际应用中，为了确保能探索环境，我们通常要求策略永远不会变成决定性的，即$\pi (a|s,\theta )\in (0,1)$对于所有$s,a,\theta$。在这个部分我们将介绍离散动作空间最常见的参数化，并指出它与动作价值方法相比的优势。

如果动作空间是离散的，而且不会太大，那么一种自然的、常见的参数化方法就是对每个状态-动作对 形成参数化的数值偏好$h(s,a,\theta )\in \mathbb{R}$。例如，根据指数soft-max分布，每个状态下具有最高偏好的动作被选择的概率是最高的。
$$\pi (a|s,\theta )\doteq \frac{e^{h(s,a,\theta )}}{{\sum }_b{e}^{h(s,b,\theta )}}\text{\hspace{1em}(9.2)}$$
注意，这里的分母只是要求使每个状态下的动作概率相加为1。我们把这种策略参数化称为动作偏好函数的soft-max参数化。

动作偏好函数本身可以任意参数化。例如，它们可以由深度人工神经网络(ANN)计算，其中$\theta$是网络所有连接权值的向量。或者动作偏好可以是简单的线性特征
$$h(s,a,\theta )={\theta }^T\text{x}(s,a)\text{\hspace{1em}(9.3)}$$
其使用特征向量$\text{x}(s,a)\in {\mathbb{R}}^{d^{\prime }}$。

根据动作偏好函数中的soft-max函数对策略进行参数化的一个好处是，近似策略可以接近确定性策略，而在$\epsilon$-贪婪的动作选择对动作值的选择中，总是存在着以概率$\epsilon$选择随机动作。当然，人们可以根据基于动作值的soft-max分布进行选择，但仅此一点就不能使策略接近确定性策略。相反，动作值的估计值将趋近于其相应的真实值，而真实值将以一种有限的量来衡量，转化为0和1之间的特定概率。如果soft-max分布包括一个温度参数，那么温度可以随着时间而降低，以接近其实际的值。但在实践中，如果没有比我们希望的假设更多的关于真实动作值的先验数据，那么将很难选择一个能使参数减少的动作规划，或者是选择一个合适的初始温度。动作偏好函数是不同的，因为它们并不接近特定的值，而是被驱动着产生最优的随机策略 。如果最优策略是确定性的，那么最优动作的偏好将被驱动到无限高于所有次优动作（如果参数化允许的话）。

根据动作偏好函数中的soft-max参数化策略的第二个优点是，它允许以任意概率选择动作。在重要函数逼近问题中，最佳近似策略可能是随机的。例如，在信息不完全的纸牌游戏中，最优的玩法通常是用特定的概率做两种不同的事情。动作-价值方法没有找到随机最优策略的自然方法，而策略近似方法可以。

与动作值参数化相比，策略参数化可能具有的最简单的优势是，策略可能是一个更简单的函数，可以近似。各种问题在其策略和动作值函数的复杂性上有所不同。对于一些问题，动作值函数更简单，因此更容易近似。对于另一些问题，策略更简单。在后一种情况下，基于策略的方法通常会学习得更快，并产生更优的渐近策略。

最后，我们注意到策略参数化的选择有时是将预期策略形式的先验知识注入到强化学习系统的一种好方法。这通常是使用基于策略的学习方法的最重要的原因。

9.2 策略梯度定理

除了策略参数化相对于$\epsilon$-贪婪的行动选择 的实际优势外，还有一个重要的理论优势。在连续策略参数化中，动作概率作为学习参数的函数平滑变化，而在$\epsilon$-贪婪选择中，动作概率可能会因为估计动作值的任意微小变化而发生剧烈变化，如果这种变化导致另一个动作具有最大值的话。主要是因为这个原因，策略梯度方法比行动值方法有更强的收敛保证。特别是，正是由于策略对参数的依赖性的连续性，使得策略梯度方法能够近似于梯度上升（9.1）。

事件性和持续性案例以不同方式定义了性能度量，$J(\theta )$， 因此在某种程度上必须要分开对待。然而，我们将统一地介绍这两种情况，并发展一种符号，以便主要的理论结果可以用单一的一组方程来描述。

在这个部分我们考虑事件性任务，其中我们定义性能度量作为时间开始状态的值。我们可以在不丢失任何有意义的概论的情况下来简化符号，通过假设每个事件开始于一些特别的状态$s_0$(非随机)。然后，在事件性任务中我们定义性能为
$$J(\theta )\doteq v_{{\pi }_{\theta }}(s_0)\text{\hspace{1em}(9.4)}$$
其中$v_{{\pi }_{\theta }}$是${\pi }_{\theta }$的真值函数，策略由$\theta$确定。从这里开始，在我们的讨论中，我们将假设在事件性任务中不使用折扣（$\gamma =1$），但为了完整性，我们在封装算法中包含了折扣的选项。

在函数近似的情况下，以确保改进的方式改变策略参数似乎具有挑战性。问题在于，性能取决于行动选择和这些选择的状态分布，而这两者都受策略参数的影响。给定一个状态，策略参数对行动的影响，从而对奖励的影响，可以通过参数化的知识以相对简单的方式计算出来。但是策略对状态分布的影响是环境的函数，通常是未知的。当梯度取决于策略变化对状态分布的未知影响时，我们如何估计性能梯度 与策略参数 的关系呢？

在这里有一个很好的理论答案，即策略梯度定理（The Policy Gradient Theorem），它提供了一个关于策略参数的性能梯度的分析表达式，它不涉及状态分布的变化。偶发情况下的策略梯度定理确定了
$$\nabla J(\theta )\propto \sum _s\mu (s)\sum _a{q}_{\pi }(s,a)\nabla \pi (a|s,\theta )\text{\hspace{1em}(9.5)}$$
其中，梯度是部分导数的列向量，与$\theta$的分量有关，$\pi$表示对应于参数向量$\theta$的策略。这里的符号$\propto$表示 “比例”。在事件性情况下，比例的常数为一个事件的平均长度，而在持续的情况下是1，所以这种关系实际上是一种相等关系。这里的$\mu$分布是策略$\pi$下on-policy分布。关于策略梯度定理的证明见9.2.2 策略梯度定理的证明。

9.2.1 梯度上升和黑箱优化

梯度上升 是迭代算法，被用作寻找最佳策略的权重$\theta$。其算法如下，

每次迭代，

• 在当前最佳权重${\theta }_{best}$附近随机选择一些值 ，然后得到一系列新的权重${\theta }_{new}$。
• 在新的一轮事件中将使用新的权重${\theta }_{new}$来获得相应的结果。如果新的权重中产生的结果大于之前权重产生的结果，则${\theta }_{best}\leftarrow {\theta }_{new}$。

梯度上升算法可以被归类为黑箱优化（black-box optimization）技术。黑盒（black-box）是旨在求得使函数$J=J(\theta )$获得最大值的权重$\theta$，我们只需要估计在任何潜在值$\theta$下的$J$的值。

也就是说，梯度上升等算法是不知道我们在解决一个强化学习问题的，其也不关心我们试图最大化的函数是否与预期奖励相对应。这些算法只知道，对于每个$\theta$的取值，有一个对应的数字。我们知道这个数字 对应于通过使用$\theta$的相关策略收集一个事件后而获得的奖励，但是算法并不知道这一点。对于算法来说，我们计算$\theta$的方法被认为是一个黑盒。这些算法只关心求出会使黑盒中数值最大化的$\theta$的值。

下面介绍一些黑箱优化算法：

• 最速梯度上升（Steepest ascent hill climbing） 是梯度上升算法的一种变体，它在每次迭代中选择少量的临近策略，并从中选择最优的策略。
• 模拟退火（Simulated annealing） 是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能。
• 自适应噪声缩放（Adaptive noise scaling） 是随着每次迭代找到新的最佳策略后减小搜索半径，反之则增大搜索半径。
• 交叉熵方法（cross-entropy method） 迭代地建议少量的相邻策略，并使用少量的最佳执行策略来计算一个新的估计。
• 进化策略（evolution strategies） 考虑每个候选策略对应的返回值。下一次迭代的策略估计是所有候选策略的加权和，其中获得更高奖励的策略被给予更高的权重。

9.2.2 策略梯度定理的证明

只需要基本的微积分和项的重排，我们就可以从第一原理证明策略梯度定理。为了保持简单的符号，我们在所有情况下都隐含着$\pi$是$\theta$的函数。，所有的梯度也都隐含在关于$\theta$的函数中。首先请注意，状态价值函数的梯度可以用动作值函数来描述
$$\begin{array}{rl}\nabla v_{\pi }(s)& =\nabla [\sum _a\pi (a|s)q_{\pi }(s,a)],\text{ for all }s\in \mathcal{S}\\ & =\sum _a[\nabla \pi (a|s)q_{\pi }(s,a)+\pi (a|s)\nabla q_{\pi }(s,a)]\text{ (product rule of calculus)}\\ & =\sum _a[\nabla \pi (a|s)q_{\pi }(s,a)+\pi (a|s)\nabla \sum _{s^{\prime },r}p(s^{\prime },r|s,a)(r+v_{\pi }(s^{\prime }))]\\ & =\sum _a[\nabla \pi (a|s)q_{\pi }(s,a)+\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)\nabla v_{\pi }(s^{\prime })]\\ & =\sum _a[\nabla \pi (a|s)q_{\pi }(s,a)+\pi (a|s)\sum _{s^{\prime }}p(s^{\prime }|s,a)\sum _{a^{\prime }}[\nabla \pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime })+\pi (a^{\prime }|s^{\prime })\sum _{s^{\prime \prime }}p(s^{\prime \prime }|s^{\prime },a^{\prime })\nabla v_{\pi }(s^{\prime \prime })]]\\ & =\sum _{s\in \mathcal{S}}\sum _{k=0}^{\infty }\text{Pr}(s\to x,k,\pi )\sum _a\nabla \pi (a|x)q_{\pi }(x,a)\end{array}$$
在多次展开后，其中$\text{Pr}(s\to x,k,\pi )$是策略$\pi$下以$k$步从状态$s$转换为状态$x$的概率。然后有
$$\begin{array}{rl}\nabla J(\theta )& =\nabla v_{\pi }(s_0)\\ & =\sum _s(\sum _{k=0}^{\infty }\text{Pr}(s\to x,k,\pi ))\sum _a\nabla \pi (a|x)q_{\pi }(x,a)\\ & =\sum _s\eta (s)\sum _a\nabla \pi (a|x)q_{\pi }(x,a)\\ & =\sum _s\eta (s^{\prime })\sum _s\frac{\eta (s)}{{\sum }_{s^{\prime }}\eta (s^{\prime })}\sum _a\nabla \pi (a|x)q_{\pi }(x,a)\\ & =\sum _s\eta (s^{\prime })\sum _s\mu (s)\sum _a\nabla \pi (a|x)q_{\pi }(x,a)\\ & \propto \sum _s\mu (s)\sum _a\nabla \pi (a|s)q_{\pi }(s,a)\end{array}$$

9.3 REINFORCE:蒙特卡洛策略梯度

现在来推导第一个策略梯度学习算法。之前说到的随机梯度上升的总体策略(9.1)，它需要一种获得样本的方法，使样本梯度的期望值与性能测量的实际梯度成正比，作为参数的函数。样本梯度只需与梯度成正比即可，因为任何比例常数都可以被吸收到步长大小中 ，否则步长大小是任意的。策略梯度定理给出了一个与梯度成正比的精确表达式；所需要的是一些期望值等于或接近这个表达式的抽样方式。请注意，策略梯度定理的右侧是对状态的加权和，加权后的状态在目标策略下出现的频率；如果按照这个比例，那么状态将以这些比例出现。因此
$$\begin{array}{rl}\nabla J(\theta )& \propto \sum _s\mu (s)\sum _a{q}_{\pi }(s,a)\nabla \pi (a|s,\theta )\\ & ={\mathbb{E}}_{\pi }[\sum _a{q}_{\pi }(S_t,a,\text{w})\nabla \pi (a|S_t,\theta )]\end{array}\text{\hspace{1em}(9.6)}$$
实例化我们的随机梯度上升算法(9.1)为
$${\theta }_{t+1}\doteq {\theta }_t+\alpha \sum _a\hat{q}(S_t,a,\text{w})\nabla \pi (a|S_t,\theta )\text{\hspace{1em}(9.7)}$$

$\hat{q}$是$q_{\pi }$的一些优化后的近似值。这个算法,它被称为一个all-action方法,因为它更新涉及到的所有行动。我们主要针对于经典REINFORCE算法(Willams, 1992)， 其在时间$t$的更新只涉及$A_t$，即在时间$t$实际采取的一个行动。

继续对REINFORCE的推导，以与(9.6)中引入$S_t$相同的方式引入$A_t$，将随机变量的可能值之和替换为策略$\pi$下的期望值，然后对期望值进行抽样。式(9.6)涉及到一个适当的动作和，但是每个项并没有像$\pi$下的期望值那样被$\pi (a|S_t,\theta )$加权。所以我们在不改变相等的前提下，引入这样的加权，通过将和项乘以然后除以$\pi (a|S_t,\theta )$。接(9.6)，我们得到了以下结果

$$\begin{array}{rl}\nabla J(\theta )& ={\mathbb{E}}_{\pi }[\sum _a\pi (a|S_t,\theta )q_{\pi }(S_t,a)\frac{\nabla \pi (a|S_t,\theta )}{\pi (a|S_t,\theta )}]\\ & ={\mathbb{E}}_{\pi }[q_{\pi }(S_t,A_t)\frac{\nabla \pi (A_t|S_t,\theta )}{\pi (A_t|S_t,\theta )}]\text{ (replacing }a\text{ by sample }{A}_t\to \pi )\\ & =G_t\frac{\nabla \pi (A_t|S_t,\theta )}{\pi (A_t|S_t,\theta )}]\text{ (beacuse }{\mathbb{E}}_{\pi }[G_t|S_t,A_t]=q_{\pi }(S_t,A_t))\end{array}$$
其中$G_t$是奖励。括号中的最后一个表达式正是我们所需要的，一个可以在每个时间步上采样的量，其期望值等于梯度。使用这个样本来实例化我们的通用随机梯度上升算法(9.1)，可以得到REINFORCE更新结果
$${\theta }_{t+1}\doteq {\theta }_t+\alpha G_t\frac{\nabla \pi (A_t|S_t,{\theta }_t)}{\pi (A_t|S_t,{\theta }_t)}\text{\hspace{1em}(9.8)}$$

这个更新有一个直观的吸引力。每一次增量都与奖励率$G_t$和一个向量的乘积成正比，即采取实际行动的概率梯度除以采取该行动的概率。该向量是参数空间中最能增加未来访问状态$S_t$时重复行动$A_t$的概率的方向，更新后该方向的参数向量增加与奖励成正比，与行动概率成反比。前者是有意义的，因为它使参数向有利于产生最高收益的行动的方向移动最多。后者之所以有意义，是因为否则频繁被选择的行动处于优势（更新将更频繁地朝它们的方向进行），即使它们没有产生最高的奖励，也可能胜出。

请注意，REINFORCE使用的是时间下$t$的完整奖励，其中包括直到事件结束前的所有未来奖励。在这个意义上，REINFORCE是一个蒙特卡洛算法，并且只针对情节完成后所有更新都是在回顾中进行的的事件情况下定义良好。如下提供了相关的伪代码,

---

REINFORCE: 对于${\pi }_{\ast }$蒙特卡罗策略梯度控制 (事件性)

---

注意到最后一行伪代码中的更新与REINFORCE更新规则(9.8)显得相当不同。其中一个不同之处是，伪代码对(9.8)中的分数向量$\frac{\nabla \pi (A_t|S_t,{\theta }_t)}{\pi (A_t|S_t,{\theta }_t)}$使用了紧凑表达式$\nabla \ln \pi (A_t|S_t,{\theta }_t)$。这两个向量的表达式是等价的，这一点从恒等式$\nabla \ln x=\frac{\nabla x}{x}$中可以看出。 这个向量在文献中被赋予了多种名称和符号，我们将简单地把它称为资格向量(eligibility vector)。

伪码更新与REINFORCE更新公式（9.8）的第二个区别是，前者包含了${\gamma }^t$的系数。这是因为，在文中我们处理的是不适用折扣情况（$\gamma =1$），而在上面的算法中，我们给出的是一般使用折扣的的算法。所有的想法在使用折扣的情况下都能通过适当的调整，但涉及额外的复杂性，分散了对主要想法的注意力。

作为一种随机梯度方法，REINFORCE具有良好的理论收敛特性。通过构造，一个事件的预期更新与性能梯度方向相同。这就保证了在足够小的情况下，预期性能会有所提高，在标准随机近似条件下，在递减的情况下会收敛到局部最优。然而，作为一种蒙特卡罗方法，REINFORCE可能是高方差的，因此可能学习的过程十分缓慢。此外
$$\nabla \ln \pi (a|s,\theta )=\text{x}(s,a)-\sum _b\pi (b|s,\theta )\text{x}(s,b)\text{\hspace{1em}(9.9)}$$

9.3.1 轨迹上的REINFORCE算法

将以上方法推广到一个新的概念上，在这里使用轨迹(trajectory)$\tau$作为状态-动作序列$s_0,a_0,\dots ,s_H,a_H,s_{H+1}$。其中$H$为轨迹的范围。那这里为什么要使用轨迹，而不是事件（episode）？因为使用轨迹可以使我们在整个轨迹中寻找最大值，因此可以为事件性和连续性任务找出相应的最佳策略。
类似于公式
$$\begin{array}{rl}\nabla J(\theta )& =G_t\frac{\nabla \pi (A_t|S_t,\theta )}{\pi (A_t|S_t,\theta )}]\\ & =G_t\nabla \log \pi (A_t|S_t,\theta )\end{array}$$
有期望值

$$U(\theta )=\sum _{\tau }\mathbb{P}(\tau ;\theta )R(\tau )$$

使用似然比策略梯度（ likelihood ratio policy gradient）：
$${\nabla }_{\theta }U(\theta )=\sum _{\tau }\mathbb{P}(\tau ;\theta ){\nabla }_{\theta }\log \mathbb{P}(\tau ;\theta )R(\tau )$$
其中，类比于将奖励$R(\tau )$作为轨迹$\tau$的函数来替代$G_t$。然后，我们计算返回$R(\tau )$可以取的所有可能值的加权平均值(权重由$\mathbb{P}(\tau ;\theta )$给出,以替代$\pi (A_t|S_t,\theta )$)。

我们可以用样本加权平均来近似上面的梯度,$m$为轨迹$\tau$的数量:
$${\nabla }_{\theta }U(\theta )\approx \frac{1}{m}\sum _{i=1}^m{\nabla }_{\theta }\log \mathbb{P}({\tau }^{(i)};\theta )R({\tau }^{(i)})$$
其中
$${\nabla }_{\theta }\log \mathbb{P}({\tau }^{(i)};\theta )=\sum _{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }(a_t^{(i)}|s_t^{(i)})$$

$H$为轨迹$\tau$的范围。

带入原式可以得到
$${\nabla }_{\theta }U(\theta )\approx \hat{g}:=\frac{1}{m}\sum _{i=1}^m\sum _{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }(a_t^{(i)}|s_t^{(i)})R({\tau }^{(i)})\text{\hspace{1em}(9.10)}$$

我们的目标是找到神经网络权重$\theta$的值，最大化奖励$U(\theta )={\sum }_{\tau }\mathbb{P}(\tau ;\theta )R(\tau )$。其中$\tau$是任意的轨迹。一个找到最大$\theta$的值的方法是通过梯度上升（gradient ascent） 算法。在每个循环中使用如下的梯度上升优化策略
$$\theta \leftarrow \theta +\alpha {\nabla }_{\theta }U(\theta )$$
REINFORCE伪代码(使用轨迹$\tau$)

1. 使用策略${\pi }_{\theta }$来收集$m$个轨迹${\tau }^{(1)},{\tau }^{(2)},\dots ,{\tau }^{(m)}$，其中轨迹的范围为$H$。对于第$i$个轨迹我们定义为${\tau }^{(i)}=(s_0^{(i)},a_0^{(i)},\dots ,s_H^{(i)},a_H^{(i)},s_{H+1}^{(i)})$
2. 使用轨迹来估计梯度${\nabla }_{\theta }U(\theta )$:
   ${\nabla }_{\theta }U(\theta )\approx \hat{g}:=\frac{1}{m}{\sum }_{i=1}^m{\sum }_{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }(a_t^{(i)}|s_t^{(i)})R({\tau }^{(i)})$
3. 更新策略的权重:
   $\theta \leftarrow \theta +\alpha \hat{g}$
4. 重复步骤1-3

9.3.2 REINFORCE算法实例

在这个实例中，我们使用CartPole-v0环境。

在gym官网是这样介绍的：

A pole is attached by an un-actuated joint to a cart, which moves along a frictionless track. The system is controlled by applying a force of +1 or -1 to the cart. The pendulum starts upright, and the goal is to prevent it from falling over. A reward of +1 is provided for every timestep that the pole remains upright. The episode ends when the pole is more than 15 degrees from vertical, or the cart moves more than 2.4 units from the center.

一根杆子通过一个无动力的关节连接到一个小车上，小车沿着无摩擦的轨道移动。通过对小车施加一个+1或-1的力来控制系统。摆杆开始时是直立的，目标是防止它倒下。每当杆子保持直立的时候，就会提供+1的奖励。当杆子与垂直度超过15度，或小车从中心移动超过2.4个单位时，该事件结束。

使用REINFORCE算法实现如下，

import gym
import numpy as np
from collections import deque
import matplotlib.pyplot as plt
import os

import torch
torch.manual_seed(0) # set random seed
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Categorical


class Policy(nn.Module):
    def __init__(self, s_size=4, h_size=16, a_size=2):
        super(Policy, self).__init__()
        self.fc1 = nn.Linear(s_size, h_size)
        self.fc2 = nn.Linear(h_size, a_size)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return F.softmax(x, dim=1)

    def act(self, state):
        state = torch.from_numpy(state).float().unsqueeze(0).to(device)
        probs = self.forward(state).cpu()
        m = Categorical(probs)
        action = m.sample()
        return action.item(), m.log_prob(action)


def reinforce(n_episode=1000, max_t=1000, gamma=1.0, print_every=100):
    scores_deque = deque(maxlen=100)
    scores = []
    for i_episode in range(1, n_episode+1):
        saved_log_porbs = []
        rewards = []
        state = env.reset()
        for t in range(max_t):
            action, log_prob = policy.act(state)
            saved_log_porbs.append(log_prob)
            state, reward, done, _ = env.step(action)
            rewards.append(reward)
            if done:
                break
        scores_deque.append(sum(rewards))
        scores.append(sum(rewards))

        discounts = [gamma**i for i in range(len(rewards)+1)]
        R = sum([a*b for a,b in zip(discounts, rewards)])

        policy_loss = []
        for log_prob in saved_log_porbs:
            policy_loss.append(-log_prob * R)
        policy_loss = torch.cat(policy_loss).sum()

        optimizer.zero_grad()
        policy_loss.backward()
        optimizer.step()

        if i_episode % print_every == 0:
            print('Episode {}\t Average Score: {:.2f}'.format(i_episode, np.mean(scores_deque)))
        if np.mean(scores_deque) >=195.0:
            print('Environment solved in {:d} episode!\tAverage Score:{:.2f}'.format(i_episode-100, np.mean(scores_deque)))
            break

    return scores

os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
env = gym.make('CartPole-v0')
env.seed(0)
print('observation space:', env.observation_space)
print('action space:', env.action_space)
policy = Policy().to(device)
optimizer = optim.Adam(policy.parameters(), lr=1e-2)
scores = reinforce()

fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(1, len(scores)+1), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()

env = gym.make('CartPole-v0')

state = env.reset()
for t in range(1000):
    action, _ = policy.act(state)
    env.render()
    state, reward, done, _ = env.step(action)
    if done:
        break

env.close()

程序说明

class Policy(nn.Module):
    def __init__(self, s_size=4, h_size=16, a_size=2):
        super(Policy, self).__init__()
        self.fc1 = nn.Linear(s_size, h_size)
        self.fc2 = nn.Linear(h_size, a_size)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = self.fc2(x)
        return F.softmax(x, dim=1)

    def act(self, state):
        state = torch.from_numpy(state).float().unsqueeze(0).to(device)
        probs = self.forward(state).cpu()
        m = Categorical(probs)
        action = m.sample()
        return action.item(), m.log_prob(action)

在这里建立了一个关于策略的全连接神经网络，输入层为4，中间层为16，输出层为2。其中输入层和输出层的节点个数是由CartPole环境定义的。像之前一样，函数中定义了初始化函数__init__和前向传播函数__forward__。与之前DQN中定义不同的是，这里定义了act函数。其作用为建立以probs为概率分布的类别分布，对其采样获得相应的动作。act函数返回采样后的动作和log采样的值。log_prob()依据以下函数定义，
$$\Delta \theta =\alpha r\frac{\partial \log p(a|{\pi }^{\theta }(s))}{\partial \theta }$$
其中$\theta$是参数，$\alpha$是学习率，$r$是奖励，$\text{p}(a|{\pi }^{\theta }(s))$是在策略${\pi }^{\theta }$下$s$状态采取动作$a$的概率。根据公式(9.10)可以得到这个部分计算${\nabla }_{\theta }\log {\pi }_{\theta }(A_t,S_t)$的值。

---

def reinforce(n_episode=1000, max_t=1000, gamma=1.0, print_every=100):
	scores_deque = deque(maxlen=100)
	...

此处定义了整个REINFORCE的核心算法。在这里我们定义了最大的训练事件数，和最大的轨迹范围

        discounts = [gamma**i for i in range(len(rewards)+1)]
        R = sum([a*b for a,b in zip(discounts, rewards)])

        policy_loss = []
        for log_prob in saved_log_porbs:
            policy_loss.append(-log_prob * R)
        policy_loss = torch.cat(policy_loss).sum()

我们使用以上的部分来计算当前策略的损失。使用前面推导出的公式（9.10）
$${\nabla }_{\theta }U(\theta )\approx \hat{g}:=\frac{1}{m}\sum _{i=1}^m\sum _{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }(a_t^{(i)}|s_t^{(i)})R({\tau }^{(i)})$$
R即为$R(\tau )$，我们就可以得出在整条轨迹上的损失policy_loss,即${\sum }_{t=0}^H{\nabla }_{\theta }\log {\pi }_{\theta }(a_t^{(i)}|s_t^{(i)})R({\tau }^{(i)})$。此处轨迹$\tau$只有一条，所以$m=1$。

当100轮内的损失的平均值大于195时，我们就可以认为这个任务已经完成

---

输出为

observation space: Box(4,)
action space: Discrete(2)
Episode 100	 Average Score: 34.47
Episode 200	 Average Score: 66.26
Episode 300	 Average Score: 87.82
Episode 400	 Average Score: 72.83
Episode 500	 Average Score: 172.00
Episode 600	 Average Score: 160.65
Episode 700	 Average Score: 167.15
Environment solved in 691 episode!	Average Score:196.69

9.4 带基线的REINFORCE算法

策略梯度定理(9.5)可以推广为包括行动值与任意基线$b(s)$的比较。
$$\nabla J(\theta )\propto \sum _s\mu (s)\sum _a(q_{\pi }(s,a)-b(s))\nabla \pi (a|s,\theta )\text{\hspace{1em}(9.10)}$$
基线可以是任何函数，甚至是随机变量，只要它不随$a$变化;方程仍然有效，因为减去的量为零:
$$\sum _{a}b(s)\nabla \pi (a|s,\theta )=b(s)\nabla \sum _a\pi (a|s,\theta )=b(s)\nabla 1=0$$
使用带有基线(9.10)的策略梯度定理，可以使用与上一节类似的步骤来派生更新规则。我们最终使用的更新规则是一个新的版本的REINFORCE，它包括一个通用的基线:
$${\theta }_{t+1}\doteq {\theta }_t+\alpha (G_t-b(S_t))\frac{\nabla \pi (A_t|S_t,{\theta }_t)}{\pi (A_t|S_t,{\theta }_t)}\text{\hspace{1em}(9.11)}$$
因为基线可以统一为零，所以这种更新是REINFORCE的严格概括。一般来说，基线使更新的期望值不变，但它可以对其方差产生很大的影响。例如，我们在2.8节中看到，类似的基线可以显著降低梯度匪徒算法的方差（从而加快学习速度）。在强盗算法中，基线只是一个数字（到目前为止看到的奖励的平均值），但是对于MDPs来说，基线应该随着状态而变化。在某些状态下，所有的行动都有高值，我们需要一个高基线来区分高值行动和低值行动；在其他状态下，所有的行动都会有低值，低基线是合适的。

基线的一个自然选择是对状态值的估计，$\hat{v}(S_t,\text{w})$，其中$\text{w}\in {\mathbb{R}}^m$是学习的权重向量。因为REINFORCE是一种学习策略参数的Monte Carlo方法， ，所以似乎很自然地也要使用Monte Carlo方法来学习状态值权重，$\text{w}$，下面的方框中给出了一个完整的带基线REINFORCE的伪代码算法，使用这样一个学习的状态值函数作为基线。

---

带基线REINFORCE算法(事件性),用于估计${\pi }_{\theta }\approx {\pi }_{\ast }$

这个算法有两个步长大小，分别表示为${\alpha }^{\theta }$和${\alpha }^{\text{w}}$（其中是(9.11)中的）。选择值的步长大小（这里是${\alpha }^{\text{w}}$）相对容易；在线性情况下，我们有设置它的经验法则，如$\text{w}=0.1/\mathbb{E}[||\nabla \hat{v}(S_t,\text{w})|{|}_{\mu }^2]$（见9.6节）。如何设置策略参数的步长大小就不是很好确定了，其最佳值取决于奖励的变化范围和策略参数化。

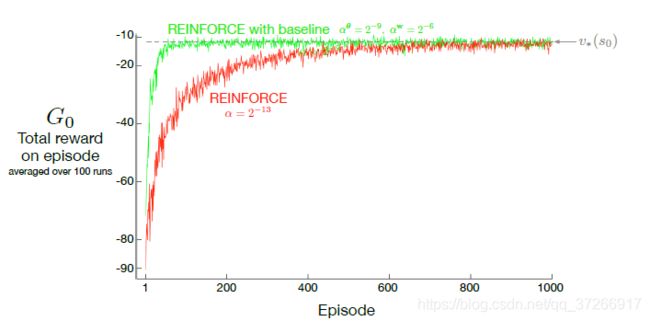
上图比较了REINFORCE在"short-corridor gridword"任务上有无基线的结果（例9.1）。这里基线中使用的近似状态值函数是$\hat{v}(S_t,\text{w})=w$.也就是说，$\text{w}$是一个单一的分量，$w$。

在接下来的博客中,将主要探讨一下REINFORCE算法的优化。