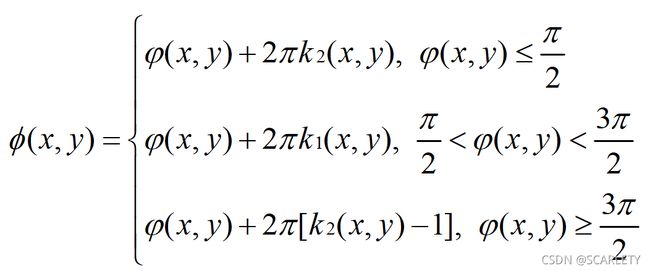(超详细)互补格雷码+相移码求解包裹相位(Python实现)
一、简介
这是我来csdn的第一篇博文,来记录我实现“互补格雷码+相移码”求解包裹相位的编码过程。也可以叫它“5+4”法,5代表五幅格雷码图像,4代表四步相移法的四张正弦条纹图(实验用的投影仪分辨率为1920*1080,相机分辨率为1280*720。格雷码+相移码解相位的原理可以参考:【3D视觉工坊】第十公开课:结构光编码与三维重建-哔哩哔哩。这次博客并不介绍标定和后面三维信息的匹配。(ps:代码能实现,但是写的比较粗糙,欢迎批评指正)
注:下面的所有代码需要放在一个文件夹下面才能正常运行,因为我是分模块编写的程序,文件之间有相互调用的部分
由于篇幅问题我将实验图像单独放在这篇博客里:实验图像(放在CSDN变成彩色图片了,需要转换成灰度图后再处理)
MATLAB版本代码在这里:互补格雷码+相移码求解包裹相位(Matlab实现)
我在这里将整个实现过程分为四个模块,每个模块包含原理、实现代码以及效果:
- 生成格雷码图像
- 生成四步相移图像
- 求包裹相位
- 求绝对相位(解包裹相位)
二、实现
1、生成格雷码图像
(1)原理
- 格雷码
一种二进制码制,是一种无权码,它的特点是前后相邻码值只改变一位数,这样可以减小错位误差,因此又称为最小错位误差码。下面是四位格雷码:
| 十进制数 | 普通二进制码 | 格雷码 |
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
- 生成n位格雷码
(i)传统方法生成:第一步,生成n位全零码
第二步,改变最右端的码值
第三步,改变自右起第一个“1”码元左边的码元
重复第二、三步直至得到2^n个格雷码
可以看出,传统方法不容易用代码实现,接下来介绍递归法
(ii)递归法
经过观察发现n位格雷码可以由(n-1)位格雷码得到,即
第一步:(n-1)位格雷码正序排列最左侧(前缀)补0
第二步:(n-1)位格雷码逆序排列最左侧(前缀)补1
第三步:一、二步得到结果依次排列得到n位格雷码
如:
1位:0 1
正序 00 01
逆序 11 10
2位:00 01 11 10
正序 000 001 011 010
逆序 110 111 101 100
3位:000 001 011 010 110 111 101 100
可见递归法比较容易代码实现,因此本文采用递归法生成n位格雷码
- 格雷码与普通二进制码的转换
(i)二进制码——>格雷码
二进制码与其右移一位高位补零后的数码异或后得到格雷码
如:二进制0010 --> 右移0001 -->0010 xor 0001 --> 格雷码0011
(ii)格雷码——>二进制码
最左边的一位不变,从左边第二位起,将每位与左边一位解码后的值异或,作为该位解码后的值。依次异或,直到最低位。依次异或转换后的值(二进制数)就是格雷码转换后二进制码的值。
如:格雷码(用G表示)0011-->二进制码(用B表示)左边第一位不变0xxx-->解码的第二位G2 xor B1 =0 xor 0 -->00xx -->G3 xor B2 --> 001x -->G4 xor B3 -->0010(二进制码)
以上是传统方法,在本文中采用字典查询的方式,下面介绍.
(iii)字典查询
在生成格雷码的同时,将每一位格雷码与其对应的十进制数组成键值对储存在字典中,这样在进行二进制码-格雷码-十进制相互转换时可以直接查询字典完成比较方便.
- 由于本文采用互补格雷码的方法(互补格雷码可以消除解包裹相位时周期级次错位问题),需要4张4位格雷码的pattern和5位格雷码的第五张pattern
- 用下面程序分别生成4位和5位格雷码图取相应的pattern即可
(2)实现代码
文件名:generate_graycode_map.py
import cv2
import numpy as np
#k:把格雷码直接当初二进制对应的十进制数
#v:格雷码实际对应的十进制数
class GrayCode():
codes = np.array([])
code2k = {}
k2v = {}
v2k = {}
def __init__(self, n: int = 3):
self.n = n
self.codes = self.__formCodes(self.n)
# 从格雷码转换到k
for k in range(2 ** n):
self.code2k[self.__code2k(k)] = k
# 从格雷码转换到v
for k in range(2 ** n):
self.k2v[k] = self.__k2v(k)
# 从v转换到k(idx)
for k, v in self.k2v.items():
self.v2k[v] = k
@staticmethod #不需要实例化直接像函数一样调用(类名.方法名()来调用),定义时也不需要self,cls参数
def __createGrayCode(n: int):
'''生成n位格雷码'''
if n < 1:
print("输入数字必须大于0")
# assert (0);
# elif n == 1: #代码较长
# code = ["0", "1"]
# return code
# else:
# code = []
# code_pre = GrayCode.__createGrayCode(n - 1) #递归嵌套
# code.append("0" + idx for idx in code_pre) #解析法写for循环
# code.append("1" + idx for idx in code_pre(::-1))
# return code
else:
code = ["0", "1"]
for i in range(1, n): # 循环递归
code_lift = ["0" + idx for idx in code] # 解析法写for循环
code_right = ["1" + idx for idx in code[::-1]]
code = code_lift + code_right
return code
def __formCodes(self, n: int): #两个下划线开头表示该方法只能在类内部使用
'''生成codes矩阵'''
code_temp = GrayCode.__createGrayCode(n) #首先生成n位格雷码储存在code_temp中
codes = []
for row in range(len(code_temp[0])): #n位格雷码循环n次,
c = []
for idx in range(len(code_temp)): #循环2**n次
c.append(int(code_temp[idx][row])) #将code_temp中第idx个元素中的第row个数添加到c中
codes.append(c)
return np.array(codes, np.uint8)
def toPattern(self, idx: int, cols: int = 1920, rows: int = 1080):
'''生成格雷码光栅图'''
#assert (idx >= 0) #断言用法,确保idx >= 0
row = self.codes[idx, :] #idx表示codes的行索引
one_row = np.zeros((cols), np.uint8) #np.zeros((5),np.uint8)=array([0,0,0,0,0])一个参数是行向量,两个参数是矩阵
#assert (cols % len(row) == 0)
per_col = int(cols / len(row)) #将1280个像素分成2**n份
for i in range(len(row)):
one_row[i * per_col: (i + 1) * per_col] = row[i]
pattern = np.tile(one_row, (rows, 1)) * 255 #np.tile(a,(b,c))函数用a来重构b行c列
return pattern
def __code2k(self, k):
'''将k映射到对应的格雷码'''
col = self.codes[:, k]
code = ""
for i in col:
code += str(i)
return code
def __k2v(self, k):
'''将k映射为v'''
col = list(self.codes[:, k]) #将第k列格雷码储存在col中
col = [str(i) for i in col]
code = "".join(col) #将列表中的元素整合到一起
v = int(code,2)
return v
def store_gray_code_map_value(self):
'''将8幅256列的格雷码编码图的码值列表储存在'格雷光栅码值.txt'文件中'''
filename = '格雷光栅码值.txt'
with open(filename,'w') as fob1:
fob1.write("codes\n")
for i in g.codes:
fob1.write('长度:' + str(len(i))+ '\n')
fob1.write(str(i) + '\n')
if __name__ == '__main__': #只在本文件内运行一下代码
n = 4
g = GrayCode(n)
print("codes")
print(g.codes)
print("\ncode -> k")
print(g.code2k)
print("\nk -> v")
print(g.k2v)
print("\nv -> k")
print(g.v2k)
g.store_gray_code_map_value()
for i in range(n):
pattern = g.toPattern(i)
title ='Pattern-' + str(i)
cv2.imshow(title, pattern)
key = cv2.waitKey(0)
if key == ord('s'):
cv2.imwrite(title + '.png', pattern)
cv2.destroyWindow(title)(3)效果
- 生成的4位格雷码图像Pattern-0~3
- 生成5位格雷码的第五张
2、生成四步相移图像
(1)原理
从N步相移码说起,首先相移码的原理是利用N幅正弦条纹图通过投影仪投射到物体表面再通过相机拍摄获取图像,通过所得图像计算每个位置的相位差,然后通过相位—深度的映射关系获取物体的深度信息。
- 投影光栅的光强函数:
![]() n表示下标
n表示下标
![]()
式中:A(x,y)表示背景光强,B(x,y)表示调制幅值,![]() 表示包裹相位(相对相位),
表示包裹相位(相对相位),![]() 表示平移相位。其中前三个变量未知,因此N至少取3。
表示平移相位。其中前三个变量未知,因此N至少取3。
- 四步相移码
由于选用4位格雷码+四步相移,编码区域可以分为16,因此相移码的周期数![]() ,周期
,周期![]() ,因此
,因此![]()
T用像素表示,Width表示图像宽度(单位:像素)
实验投影仪width=1920(像素)因此T=1920/16
第一步:生成一个1920维的行向量
第二步:利用公式![]() 对每一个向量元素进行填充
对每一个向量元素进行填充
第三步:利用np.tile()函数生成1080行,得到1920*1080的矩阵
第四步:利用cv2.imshow()函数显示
(2)实现代码
文件名:generate_phase-shifting_map.py
import cv2
import numpy as np
import math
class PhaseShiftingCode():
def __init__(self,n: int = 4):
self.n = n
def toPhasePattern(self,j:int,freq:int=16,width:int=1920,hight:int=1080):
'''生成'''
col = np.zeros((width),np.uint8) #生成一个维数为width的行向量
for i in range(width):
col[i] = 128 + 127 * math.cos(2 * math.pi *( i * freq / width + j/ self.n))
pattern = np.tile(col,(hight,1))
return pattern
if __name__ == '__main__': #只在当前模块执行,其他模块导入本模块时不执行
n = 4
p = PhaseShiftingCode(n)
for k in range(n):
pattern = p.toPhasePattern(k)
title ='PhaseShifting-' + str(k)
cv2.imshow(title, pattern)
key = cv2.waitKey(0)
if key == ord('s'):
cv2.imwrite(title + '.png', pattern)
cv2.destroyWindow(title)(3)效果
PhaseShifting-0~3
3、求包裹相位
(1)原理
N步相移法求包裹相位的详细推导可以参考这篇博客:标准N步相移主值相位计算式推导过程
这里给出四步相移法的求解公式:
![]()
![]()
![]()
![]()
联立得:
![]() ,由于反正切函数被限制在
,由于反正切函数被限制在![]() ,因此该公式求解的是包裹相位
,因此该公式求解的是包裹相位
在实际的代码中我们需要考虑4个特殊位置和4个象限:
将每一个像素利用上述方法求得包裹相位并储存在对应位置,可以得到所有对应位置的数值大小都在![]() ,然后对其进行线性放缩到
,然后对其进行线性放缩到![]() ,再用cv2.imshow()显示。
,再用cv2.imshow()显示。
(2)实现代码
文件名:wrapped_phase_algorithm.py
import numpy as np
import cv2 as cv
import math
class WrappedPhase():
def __init__(self,n:int = 4):
self.n = n
@staticmethod
def getImageData(m:int = 4):
'''获取相机拍摄的n幅相移图'''
I = []
for i in range(m):
filename = r"D:\研一文件\其他\structual_light_project\left\I" + str(i+5) + ".png"
img_file = np.fromfile(filename, dtype=np.uint8) # 以dtype形式读取文件
img = cv.imdecode(img_file, -1) # 从指定的内存缓存中读取数据,并把数据转换(解码)成图像格式;主要用于从网络传输数据中恢复出图像。
I.append(img)
return I
def computeWrappedphase(self,I,width:int = 1280,hight:int = 720):
'''计算包裹相位'''
i0 = I[0].astype(np.float32)
i1 = I[1].astype(np.float32)
i2 = I[2].astype(np.float32)
i3 = I[3].astype(np.float32)
pha = np.zeros((hight,width),np.float32)
for a in range(hight):
for b in range(width):
if i0[a,b] == i2[a,b] and i3[a,b] < i1[a,b]: #四个特殊位置
pha[a,b] = 3*math.pi/2
elif i0[a,b] == i2[a,b] and i3[a,b] > i1[a,b]: #四个特殊位置
pha[a,b] = math.pi/2
elif i3[a, b] == i1[a, b] and i0[a, b] < i2[a, b]: #四个特殊位置
pha[a, b] = math.pi
elif i3[a, b] == i1[a, b] and i0[a, b] > i2[a, b]: #四个特殊位置
pha[a, b] = 0
elif i0[a, b] > i2[a, b] and i1[a,b] < i3[a,b]: # 第一象限
pha[a,b] = math.atan((i3[a,b] - i1[a, b])/ (i0[a, b] - i2[a, b]))
elif i0[a, b] < i2[a, b] and i1[a,b] < i3[a,b]: # 第二象限
pha[a,b] = math.pi-math.atan((i3[a,b] - i1[a, b])/ (i2[a, b] - i0[a, b]))
elif i0[a, b] < i2[a, b] and i1[a,b] > i3[a,b]: # 第三象限
pha[a,b] = math.pi + math.atan((i3[a,b] - i1[a, b])/ (i0[a, b] - i2[a, b]))
elif i0[a, b] > i2[a, b] and i1[a,b] > i3[a,b]: # 第四象限
pha[a,b] = 2*math.pi - math.atan((i1[a,b] - i3[a, b])/ (i0[a, b] - i2[a, b]))
pha_scaled = pha*255/(2*math.pi)
pha_scaled1 = pha_scaled.astype(np.uint8)
if __name__ == "__main__":
cv.imshow("Wrapped_Phase",pha_scaled1)
key = cv.waitKey(0)
if key == ord("s"):
cv.imwrite("Wrapped_Phase.png",pha_scaled1)
cv.destroyAllWindows()
return pha
if __name__ == "__main__":
w = WrappedPhase()
w.computeWrappedphase(w.getImageData())(3)效果
4、求绝对相位
(1)原理
- 现在我们已经获得了包裹相位
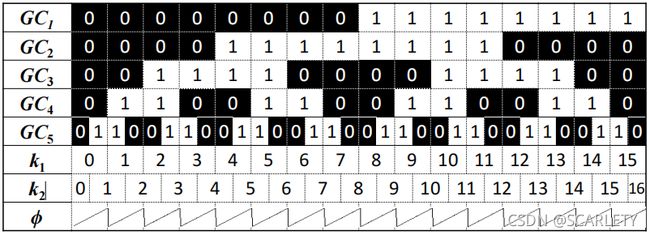
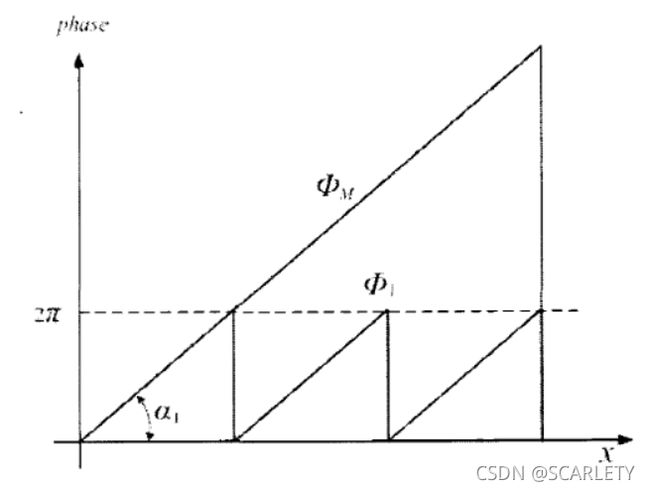
 如类似上图(途中GC表示格雷码图,k1、k2表示对应的编码值),现在我们需要将上面的包裹相位还原成连续的绝对相位。我们发现,只要在每一个截断处加上
如类似上图(途中GC表示格雷码图,k1、k2表示对应的编码值),现在我们需要将上面的包裹相位还原成连续的绝对相位。我们发现,只要在每一个截断处加上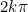 (k表示周期的级次),就可以恢复成连续的相位:
(k表示周期的级次),就可以恢复成连续的相位:
- 因此我们用四幅格雷码图像将整个有效视区分成16份并分别编码,因此这里的周期级次K就等于格雷码的编码值(k1),但是由于实际过程中,由于投影仪和相机的畸变效应,所投的格雷码图像与相移码图像会产生错位:
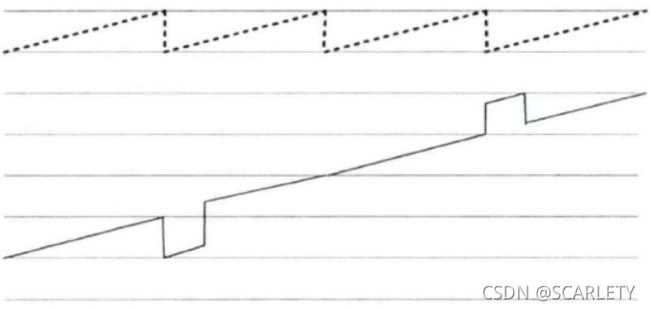
- 由于错位发生在包裹相位的截断处,为了解决错位问题,我们引入一张5位格雷码,与4位格雷码形成互补,k2的计算公式如下:
![]()
INT:向下取整,V2:GC0-GC5格雷码对应的十进制数。
利用以下公式就可以避免截断处产生错位:
- 在相机实际拍摄的图片中由于环境光的影响,拍摄到的格雷码值并不是标准的二值图,因此我们首先要将格雷码图像进行二值化处理
(i)选取二值化阈值:利用四幅相移码图像每个像素的均值作为阈值获得阈值图像TH_img
(ii)将每一幅格雷码图像与阈值图的每一个对于对应像素进行对比,小于等于阈值赋值为0,大于阈值的赋值为1
(iii)将二值化后的图像放缩到[0,255]以显示出来
- 然后计算k1、k2的值
- 最后带入公式求解绝对相位,由于相移码分为16个周期,因此最后的绝对相位是
![[0,32\pi ]](http://img.e-com-net.com/image/info8/6f048bb242644bafb225836f5b469e4f.gif) ,再将获得的绝对相位A进行线性放缩得到B=A*255/
,再将获得的绝对相位A进行线性放缩得到B=A*255/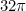 ,显示出来。
,显示出来。
(2)实现代码
首先进行图像二值化
文件名:graycode_binarization.py
import cv2 as cv
import numpy as np
import math
from wrapped_phase_algorithm import WrappedPhase
class Binariization():
def __init__(self,n:int=5):
self.n = n
def get_threshold(self,m:int = 4):
'''利用四幅相移图计算阈值'''
wp = WrappedPhase()
I = wp.getImageData(m)
i = []
for k in range(m):
i.append(I[k].astype(np.float32))
I_th = np.rint((i[0]+i[1]+i[2]+i[3])/m) #np.rint()四舍五入取整
TH = I_th.astype(np.uint8)
cv.imshow('th', TH)
key1 = cv.waitKey(0)
if key1 == ord("s"):
cv.imwrite('TH_img.png',TH)
cv.destroyAllWindows()
return TH
def get_GC_images(self):
'''读取格雷码图片'''
J = []
for i in range(5):
filename = r"D:\研一文件\其他\structual_light_project\left\I" + str(i) + ".png"
file_img = np.fromfile(filename,dtype = np.uint8)
img = cv.imdecode(file_img,-1)
J.append(img)
return J
def getBinaryGrayCode(self):
'''将格雷码图像二值化处理'''
b = Binariization()
threshold = b.get_threshold()
graycodes = b.get_GC_images()
rows,cols = threshold.shape #获取分辨率信息
for a in graycodes:
for b in range(rows):
for c in range(cols):
if a[b,c] <= threshold[b,c]:
a[b,c] = 0
else:
a[b,c] = 255
return graycodes
if __name__ == "__main__":
bgc = Binariization()
gc = bgc.getBinaryGrayCode()
for u in range(5):
gc[u].astype(np.uint8)
cv.imshow('Binarized_GC-' + str(u),gc[u])
key2 = cv.waitKey(0)
if key2 == ord('s'):
cv.imwrite('Binarized_GC-' + str(u) + ".png",gc[u])
cv.destroyAllWindows()(3)效果
阈值图像TH_img
![]()
然后求绝对相位
文件名:unwrapped_phase_algorithm.py
import numpy as np
import cv2 as cv
import math
from wrapped_phase_algorithm import WrappedPhase
from graycode_binarization import Binariization
from generate_graycode_map import GrayCode
class UnwrappedPhase():
'''获得解包裹相位'''
def __init__(self,n:int = 5):
self.n = n
def getBinarizedGrayCodes(self,m:int = 5):
'''获得二值化后的格雷码图像,m为格雷码位数'''
BGC = []
for i in range(self.n):
filename = "binarized_GC-" + str(i) + ".png"
img = np.array(cv.imread(filename, 0), np.uint8)
img_scaled = img/255
BGC.append(img_scaled.astype(np.uint8))
return BGC
def get_k1_k2(self):
'''获得k1和k2矩阵'''
BCG = self.getBinarizedGrayCodes()
rows,cols = BCG[0].shape
k1 = np.zeros((rows,cols),np.uint8)
k2 = np.zeros((rows,cols),np.uint8)
g_k1 = GrayCode(4) #调用格雷码生成模块的GrayCode()类
g_k2 = GrayCode(5)
for a in range(rows):
for b in range(cols):
code1 = ""
code_k1 = code1 + str(BCG[0][a,b]) + str(BCG[1][a,b]) + str(BCG[2][a,b]) + str(BCG[3][a,b])
code_k2 = code1 + str(BCG[0][a,b]) + str(BCG[1][a,b]) + str(BCG[2][a,b]) + str(BCG[3][a,b]) + str(BCG[4][a,b])
k1[a,b] = g_k1.code2k[code_k1] #查询字典,将格雷码转换为对应的十进制数
k2[a,b] = math.floor((g_k2.code2k[code_k2]+1)/2)
return k1,k2
def computeUnwrappedPhase(self):
'''计算解包裹相位'''
WP = WrappedPhase()
wrapped_pha = WP.computeWrappedphase(WP.getImageData())
k1,k2 = self.get_k1_k2()
rows,cols = k1.shape
unwrapped_pha = np.zeros((rows,cols),np.float16)
for c in range(rows):
for d in range(cols):
if wrapped_pha[c,d] <= math.pi/2:
unwrapped_pha[c,d] = wrapped_pha[c,d] + k2[c,d]*2*math.pi
elif wrapped_pha[c, d] > math.pi / 2 and wrapped_pha[c, d] < 3*math.pi / 2 :
unwrapped_pha[c, d] = wrapped_pha[c, d] + k1[c, d] * 2 * math.pi
elif wrapped_pha[c, d] >= 3*math.pi / 2 :
unwrapped_pha[c, d] = wrapped_pha[c, d] + (k2[c, d]-1) * 2 * math.pi
return unwrapped_pha
def showUnwrappedPhase(self):
'''显示解包裹相位'''
upha = self.computeUnwrappedPhase()
upha_scaled = np.rint(upha*255/(32*math.pi))
upha_scaled_uint = upha_scaled.astype(np.uint8)
cv.imshow("Absolute_pha.png",upha_scaled_uint)
key = cv.waitKey(0)
if key == ord("s"):
cv.imwrite("Absolute_pha.png",upha_scaled_uint)
cv.destroyAllWindows()
if __name__ == "__main__":
u = UnwrappedPhase()
u.showUnwrappedPhase()
(3)效果
====================================2021/10/14补充=========================
有同学问我关于格雷码与相移码的问题,如下:
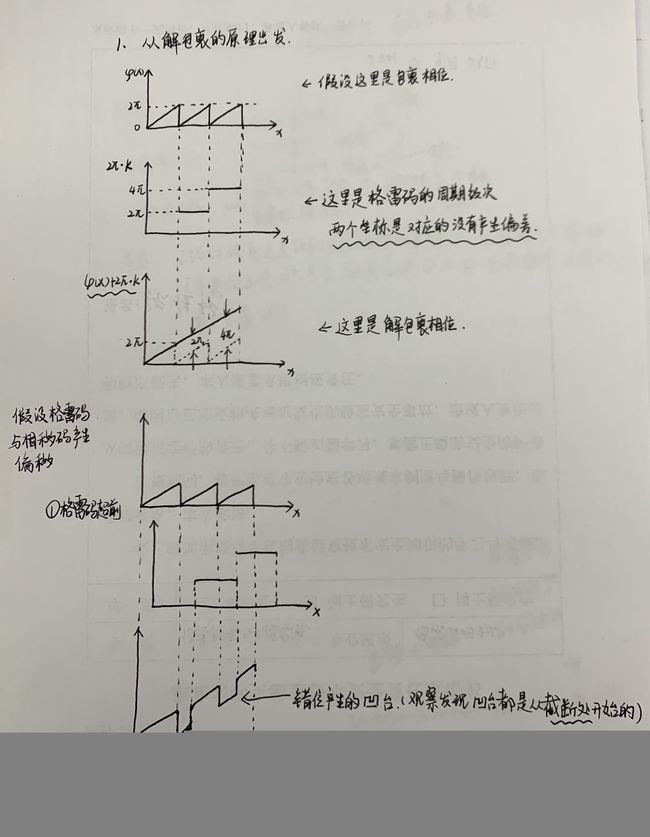
1. “解包裹相位时周期级次错位问题”怎么理解?
2. 为什么互补格雷码可以解决这个问题?
我手写了解答放在这里供大家参考
参考资料 【3D视觉工坊】第十三公开课:基于格雷码结合相移技术的高鲁棒性高效率动态三维面形测量-哔哩哔哩
单目结构光三维视觉测量系统研究_胡华虎
基于数字光栅投影的结构光三维测量技术与系统研究_李中伟
数字投影结构光三维测量方法研究_张万祯
光栅投影三维测量关键技术研究_王建华
基于编码结构光的三维测量技术研究_吴加凤