matlab8邻域搜索算法,一种基于可搜索连续邻域A*算法的路径规划方法与流程
本发明涉及的是一种UUV全局路径规划方法。
背景技术:
无人水下航行器(Unmanned underwater vehicle,UUV)作为一种高技术手段,在海洋这块未来极具价值的发展空间中起着至关重要的作用,而路径规划是自主式水下航行器的关键技术之一,是自主式水下航行器能在所处的环境中安全、有效地行驶,顺利完成给定任务的重要保证。
UUV全局路径规划本质是在规划区域内,在给定的障碍物和约束条件下,寻找一条从起始点到目标点的最优或可行的路径。传统的路径规划算法,如人工势场法、图搜索法、粒子群算法等大多有一些不足之处,例如容易陷入局部极小及计算量大等问题。在以栅格法环境建模的基础上,采用可搜索连续领域的A*算法进行UUV全局路径规划,可以有效地解决传统UUV路径规划算法容易陷入局部最优点、计算量大等问题。
技术实现要素:
本发明的目的在于提供一种能缩短UUV路径、节约时间、提高效率的基于可搜索连续邻域A*算法的路径规划方法。
本发明的目的是这样实现的:
步骤一、根据存在的障碍物采用栅格法建立环境模型获得的环境模型,对以UUV为质点、障碍物的最长宽度为直径、障碍物的重心为原点的圆形障碍物,利用公式获得各圆形障碍物的面积Si,其中li为第i障碍物的最大直径;
步骤二、根据步骤一获得的各圆形障碍物的面积,确定栅格大小l;
其中:S表示为环境的总面积,lmax是障碍物最大边长,lmin=min(lminobs,dr)是障碍物的最小边长,dr是UUV直径,l为最终确定的栅格边长;
步骤三、A*算法的估价函数为:
f(x)=g(x)+h(x)
其中,f(x)是从初始点经由x节点到目标点的估价函数,估价函数为f,g(x)是在状态空间中从初始点到x节点的实际代价,实际代价为g,h(x)是从x节点到目标点最优路径的估计代价,估价代价为h;
步骤四、根据步骤三获得的A*算法的估价函数,将每个栅格的边线定义为可访问的节点,可搜索领域A*算法的估价代价为
h(y)=d×h(X2)+(l-d)×h(X1) d∈[0 l]
其中,h(X1)为节点X1的估计代价,h(X2)为节点X2的估计代价,y是点X2X1线段上的任意一点,d是点y到X1的距离,X1,X2...X8是当前节点X的相邻的八个边线交点的节点;
步骤五、根据步骤四获得的可搜索连续领域A*算法的g值、f值和h值,依次找到优化的节点,直到目标点为止,这条路径即为最短路径。
本发明是为了解决UUV在海洋全局环境中路径规划中存在光滑度差以及路径非最短的问题而提出的。
本发明的有益效果:
通过计算障碍物所占的面积和整个环境面积,确定栅格环境的栅格大小,既避免了计算机实时处理和储存的数据增加的问题,也提高了UUV路径规划的准确度。
通过将传统的A*算法与可搜索连续领域相结合,缩短了UUV路径,节约了时间,提高了效率。
附图说明
图1为本发明中栅格环境建模示意图;
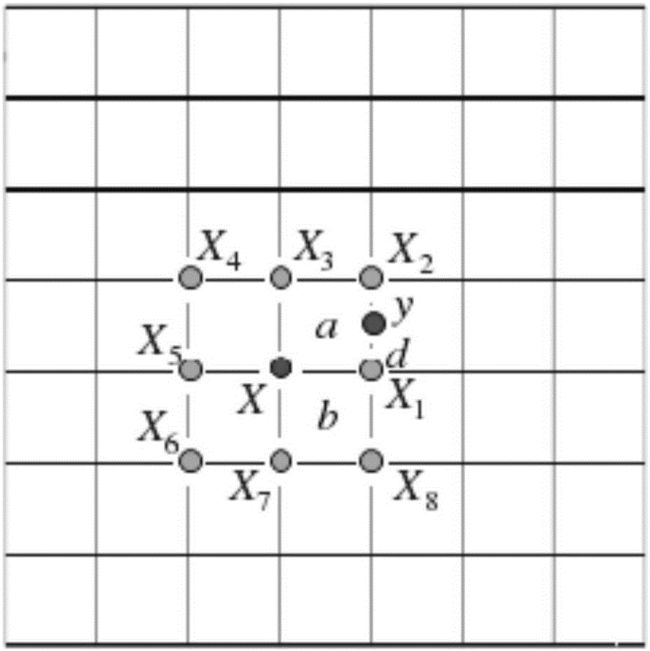
图2为本发明中可搜索领域节点是边线交点的示意图;
图3为本发明中可搜索领域节点为相邻边线与当前边线垂直的示意图;
图4为本发明中可搜索领域节点为相邻边线与当前边线平行的示意图;
图5为本发明中UUV路径规划仿真图。
具体实施方式
下面举例对本发明做更详细的描述。
结合图1、图2、图3、图4和图5,本实施方式所述的一种基于可搜索连续邻域A*算法的路径规划方法,该方法的具体步骤为:
步骤一:根据存在障碍物采用栅格法建立环境模型获得的环境模型,在地图上选取任意一个障碍物,并判断其是否为圆形;如果不是,则在第i个障碍物的所有顶点中选出在环境地图坐标系下坐标的最大值和最小值xmax,ymax,xmin,ymin,然后比较||xmax-xmin||与||ymax-ymin||获得最大直径,最后以重心为原点形成圆形障碍物。利用公式:
获得各圆形障碍物的面积Si,li为第i障碍物的最大直径。
步骤二:计算栅格的大小为
其中,S表示为环境的总面积,lmax是障碍物最大边长,lmin=min(lminobs,dr)是障碍物的最小边长,dr是移动机器人的直径,l为最终确定的栅格边长。
不考虑UUV的高度信息,将工作环境用二维平面表示,其中工作环境的东西方向为X轴,南北方向为Y轴,建立直角坐标系XOY,设二维平面的水平和垂直最大值对应在平面坐标系中为Xmax和Ymax,由于定义的栅格边长为l的正方形。
步骤三:根据已建立的栅格图,A*算法的估价函数为:
f(x)=g(x)+h(x) (4)
其中:x为节点,f(x)是从初始点经由节点到目标点的估价函数,g(x)是在状态空间中从初始点到节点的实际代价,h(x)是从节点到目标点最优路径的估计代价。当h(x)估计代价不大于节点到目标点的实际距离值时,搜索的点数多,效率低,但是能得到最优解;当h(x)大于节点到目标点的实际距离值时,搜索的点数少,效率高,但是不能保证得到最优解;对于实际环境中,可以选取两节点间的欧几里得距离直线距离)作为估计代价,即
其中(xG,yG)是目标点G的坐标,(xi,yi)是任意节点Xi的坐标。
步骤四:根据步骤三获得的A*算法的估价函数,将A*算法与可搜索连续邻域相结合,使每个栅格的边线定义为可访问的节点,一段边线上的任意点y的估计代价值h(y)是其两端点估价值的线性组合,即
h(y)=d×h(X2)+(l-d)×h(X1) d∈[0 l] (6)
其中,h(X1)为节点X1的估计代价,h(X2)为节点X2的估计代价,y是点X2X1线段上的任意一点,d是点y到X1的距离,X1,X2...X8是当前节点X的相邻的八个边线交点的节点。对于边线XXi上的代价为min(a,b)。其子节点可以是这些相邻节点中的任意一个,于是可移动方向角也就拓展为了连续任意方向。对于不同的位置节点y的g值、f值和h值不同。
当节点X是边线交点的情况时,节点X到边线X2X1上任意节点y的代价可以表示为
而
其中,g(X)是在状态空间中从初始点到X节点的实际代价,g(y)是在状态空间中从初始点到y节点的实际代价,a,b是边线XXi上的代价。
当节点X不是边线交点而是与该段边线垂直的情况时,边线节点X到边线X2X1上任意节点y的代价可以表示为
其中,t∈[0,l]而
当节点X不是边线交点节点而是与该段边线平行的情况时,边线节点X到边线X2X3上任意节点y的代价可以表示为
其中m∈[0,l],而
通过以上不同情况的计算,可以比较得到fmin和g。
步骤五:创建两个表:open表和closed表,open表用于保存所有己生成而未考察的节点,closed表用于记录己访问过不需再考察的节点。然后按照以下的步骤进行操作:
将起点A添加进open表中,并且将与A点相邻的栅格点X1,X2...X8以及边线上的任意点y添加open进表。将起点A从open表移到closed表中,并定义其为它相邻扩展的栅格的父节点。通过公式(7、8、9、10、11、12)求解open表中栅格点的g值、f值和h值。从open表中选择f值最小的栅格点,记为当前节点X,并将其从open列表移到closed表中。分别考察当前节点X的所有相邻节点(记为S,如果点既不在closed表中也不在open表中,将其添加open进表,求解其g值、f值和h值,并置当前节点X为其父节点;如果S点己经存在于open表中,则比较g(X)+c(X,S)(其中,c(X,S)为从X点到S点的代价)和g(S)的大小,当g(X)+c(X,S)<g(S)时,令g(S)=g(X)+c(X,S),并相应更新点S的f值,且置点X为其父节点,否则,则不做任何处理;如果S已经存在于closed表中,也不做任何处理。重复上述直到当前节点X为目标点G为止。从目标点G开始,依次找到其父节点,直到起点A为止,这条路径即为该算法求解出的最短路径。
具体实例:
UUV从起点(10,10)航行到终点(80,80),起始航向45°,设计了多个与障碍物O1,O2....,利用公式(1)得到障碍物的面积,利用公式(2)得到栅格的大小,利用公式(3)得到估价函数中。然后,利用可搜索连续邻域A*算法的估价函数寻找可搜索连续邻域估价函数最小的节点,作为下一航路点,逐步实现UUV航路规划。仿真轨迹如图5所示。