python-numpy-np.stack/np.vstack/np.hstack/np.dstack的用法小结
一、np.stack()
1.1 基本语法
numpy.stack(arrays, axis=0, out=None)
arrays:表示一个类数组(元组、列表、数组)的序列,可以是单个,也可以是多个(各个维度上的形状必须相同)然后用圆括号或中括号括起来。
axis:表示沿着哪个轴进行堆叠。
1.2 代码案例
首先构造以下的单个数组。
arrays = [np.arange(8).reshape(2,2,2) for _ in range(5)]
print(arrays)
print(np.shape(arrays))
# [array([[[0, 1],
# [2, 3]],
# [[4, 5],
# [6, 7]]]), array([[[0, 1],
# [2, 3]],
# [[4, 5],
# [6, 7]]]), array([[[0, 1],
# [2, 3]],
# [[4, 5],
# [6, 7]]]), array([[[0, 1],
# [2, 3]],
# [[4, 5],
# [6, 7]]]), array([[[0, 1],
# [2, 3]],
# [[4, 5],
# [6, 7]]])]
# (5, 2, 2, 2)当axis=0时,输出如下。可以看出,输出前和输出后的形状完全没有变,也就是说当axis为0时,这个函数执行之后的结果就是把原来的类数组变为纯粹的数组。
arrays = [np.arange(8).reshape(2,2,2) for _ in range(5)]
print(np.stack(arrays, axis=0))
print(np.stack(arrays, axis=0).shape)
# [[[[0 1]
# [2 3]]
# [[4 5]
# [6 7]]]
# [[[0 1]
# [2 3]]
# [[4 5]
# [6 7]]]
# [[[0 1]
# [2 3]]
# [[4 5]
# [6 7]]]
# [[[0 1]
# [2 3]]
# [[4 5]
# [6 7]]]
# [[[0 1]
# [2 3]]
# [[4 5]
# [6 7]]]]
# (5, 2, 2, 2)当axis=1时,输出如下。可以看出,输出前和输出后的形状发生改变,原来第1个维度的shape=5转移到了新的axis参数所指维度的shape上。
arrays = [np.arange(8).reshape(2,2,2) for _ in range(5)]
print(np.stack(arrays, axis=1))
print(np.stack(arrays, axis=1).shape)
# [[[[0 1]
# [2 3]]
# [[0 1]
# [2 3]]
# [[0 1]
# [2 3]]
# [[0 1]
# [2 3]]
# [[0 1]
# [2 3]]]
# [[[4 5]
# [6 7]]
# [[4 5]
# [6 7]]
# [[4 5]
# [6 7]]
# [[4 5]
# [6 7]]
# [[4 5]
# [6 7]]]]
# (2, 5, 2, 2)当axis=2时,输出如下。可以看出,输出前和输出后的形状发生改变,原来第1个维度的shape=5转移到了新的axis参数所指维度的shape上。
arrays = [np.arange(8).reshape(2,2,2) for _ in range(5)]
print(np.stack(arrays, axis=2))
print(np.stack(arrays, axis=2).shape)
# [[[[0 1]
# [0 1]
# [0 1]
# [0 1]
# [0 1]]
# [[2 3]
# [2 3]
# [2 3]
# [2 3]
# [2 3]]]
# [[[4 5]
# [4 5]
# [4 5]
# [4 5]
# [4 5]]
# [[6 7]
# [6 7]
# [6 7]
# [6 7]
# [6 7]]]]
# (2, 2, 5, 2)当axis=3时,输出如下。可以看出,输出前和输出后的形状发生改变,原来第1个维度的shape=5转移到了新的axis参数所指维度的shape上。
arrays = [np.arange(8).reshape(2,2,2) for _ in range(5)]
print(np.stack(arrays, axis=3))
print(np.stack(arrays, axis=3).shape)
# [[[[0 0 0 0 0]
# [1 1 1 1 1]]
# [[2 2 2 2 2]
# [3 3 3 3 3]]]
# [[[4 4 4 4 4]
# [5 5 5 5 5]]
# [[6 6 6 6 6]
# [7 7 7 7 7]]]]
# (2, 2, 2, 5)由于原类数组本身就只有4个维度(对应0 1 2 3),所以axis不能再升到4了。
1.3 原理讲解
这一部分主要是讲上面的四种结果是如何一步步得出来的。
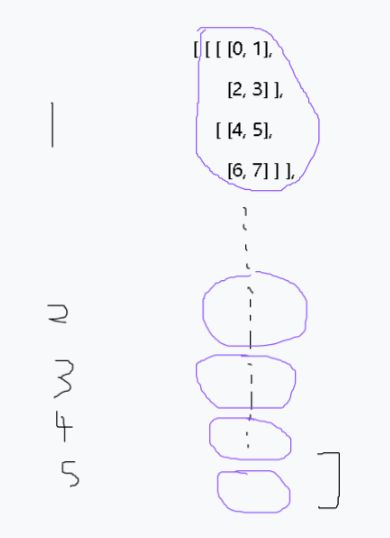
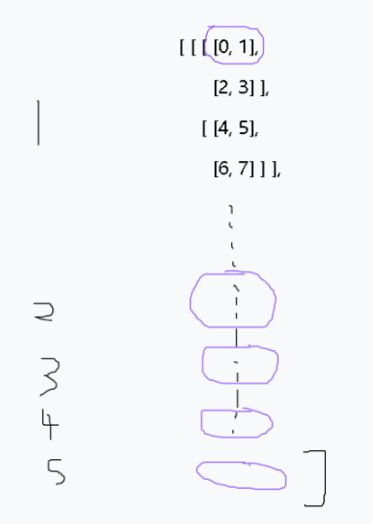
(1)当axis=0时,就是把下图中第一个中括号拆开后得到的2*2*2的数组分别看成一个整体,然后再遍历第一个维度下的指定axis的每一个整体,也即array[0, :, :, :]、array[1, :, :, :]、array[2, :, :, :]、array[3, :, :, :]、array[4, :, :, :]。最后再把这5个array组合起来。
注意,因为shape=5(dim=0),所以要遍历5次;因此最后得到的数组,axis=0对应的维度shape=5。
(2)当axis=1时,就是把下图中第一个和第二个中括号拆开后得到的2*2形状的数组分别看成一个整体。
基于这个整体对应的层级,从最外面的一维开始遍历,也即先遍历dim=0下的每一个相同层级下的所述2*2整体;
在第1个维度(从0开始)上,有两个这样的(2, )整体,但是基于顺序我们肯定先考虑前一个,也即先是遍历dim=2上索引为0的部分,对应[0, 1];
把这些整体并起来,也即array[0, 0, :, :]、array[1, 0, :, :]、array[2, 0, :, :]、array[3, 0, :, :]、array[4, 0, :, :]并起来,也就形成了5*2*2的数组;
接着,再考虑遍历第1个维度(从0开始)上剩余的整体,同理也可形成一个5*2*2的数组;
最后一步,把先前得到的两个5*2*2的数组并起来,于是就形成了2*5*2*2的数组。
(3)当axis=2时,就是把下图中第一个、第二个、第三个中括号拆开后得到的(2, )形状的数组分别看成一个整体。
先从最外面的一维开始遍历,也即先遍历dim=0中的每一个相同层级的所述(2, )整体;
在第2个维度(从0开始)上,有两个这样的(2, )整体,但是基于顺序我们肯定先考虑前一个,也即先是遍历dim=2上索引为0的部分,对应[0, 1];
把这些整体并起来,也即array[0, 0, 0, :]、array[1, 0, 0, :]、array[2, 0, 0, :]、array[3, 0, 0, :]、array[4, 0, 0, :]并起来,也就形成了5*2的数组;
再考虑遍历第2个维度(从0开始)上剩余的整体,对应[2, 3],也即把array[0, 0, 1, :]、array[1, 0, 1, :]、array[2, 0, 1, :]、array[3, 0, 1, :]、array[4, 0, 1, :]并起来,同理也可形成一个5*2的数组;
上述的这两个5*2的数组,属于同一个级别,形成了一个2*5*2的数组。
接着,再考虑遍历第1个维度(从0开始)上的第一个整体[4, 5],也即把array[0, 0, 0, :]、array[1, 0, 0, :]、array[2, 0, 0, :]、array[3, 0, 0, :]、array[4, 0, 0, :]并起来,同理也可形成一个5*2的数组;
而后,再考虑遍历第1个维度(从0开始)上的第二个整体[6, 7],也即把array[0, 1, 0, :]、array[1, 1, 0, :]、array[2, 1, 0, :]、array[3, 1, 0, :]、array[4, 1, 0, :]并起来,同理也可形成一个5*2的数组;
上述的这两个5*2的数组,属于同一个级别,形成了一个2*5*2的数组。
最后一步,把总共得到的两个2*5*2的数组并起来,于是就形成了2*2*5*2的数组。
(4)当axis=3时。我相信看到这里,大部分的读者已经懂了什么意思。
下面总结一下:
从直观的角度来看,axis对应的数字越小,原有数组保留的结构越完整,因为整体涉及到的元素和层级更多。
从抽象的角度来看,上文所述的“整体”对应的层级在各个维度上都有重复,优先遍历最外面的一维,合并之后,再遍历更高维度下的相同层级的“整体”。
原数组的第0个维度上的shape大小,一定会等于新数组axis指向的维度上的shape大小,推导时如果觉得不直观,一定优先记住这个概念。
因此,当axis=3时,新数组的形状必然是(2, 2, 2, 5),那么也就可以看成是2*2*2*5的数组。
这个数组每次都是经过了5次遍历(对应原数组第0维度的shape);
首先是遍历得到一个(5, )的子数组,然后得到2*5,接着继续得到2*2*5......
相信这样思考的话,大家的脑海中就能直观地构造出结果是什么样子了。
二、np.hstack()
2.1 语法
- numpy.hstack(tup)
- 显然,hstack和stack在调用语法上进行对比,参数只有1个。
- 这个tup参数,其实就是多个类数组(即元组、列表、数组)的组合(即用圆括号或者中括号括起来),注意这些类数组各个维度上的形状必须相同。
- 为什么没有axis参数?因为h代表水平的含义,也即沿着水平的方向进行扩展;axis默认为1,也即维度是1的shape会增大一倍。
- 但是我们也要考虑到一个特例,那就是如果原来的类数组a,b,c,...如果只有1个维度,那么这时候,维度是0的shape增大一倍。
2.2 代码示例
2.3 其他情况
numpy.hstack — NumPy v1.22 Manual参考官网教程:numpy.hstack — NumPy v1.22 Manual
三、np.vstack()
3.1 语法
- numpy.vstack(tup)
- 显然,vstack和stack在调用语法上进行对比,参数只有1个。
- 这个tup参数,其实就是多个类数组(即元组、列表、数组)的组合(即用圆括号或者中括号括起来),注意这些类数组各个维度上的形状必须相同。
- 为什么没有axis参数?因为v代表垂直的含义,也即沿着垂直的方向进行扩展;axis默认为0,也即维度是0的shape会增大一倍。
- 但是我们也要考虑到一个特例,那就是如果原来的类数组a,b,c,...如果只有1个维度,那么这时候,新数组上的维度会增加1个,并且维度是0的shape会增大一倍;比如从( , 4)到(2, 4)。
3.2 代码示例
3.3 其他情况
参考官网教程:numpy.vstack — NumPy v1.22 Manual
四、np.dtack()
4.1 语法
- numpy.dstack(tup)
- 显然,dstack和stack在调用语法上进行对比,参数只有1个。
- 这个tup参数,其实就是多个类数组(即元组、列表、数组)的组合(即用圆括号或者中括号括起来),注意这些类数组各个维度上的形状必须相同。
- 为什么没有axis参数?因为d代表深度的含义,也即沿着深度的方向进行扩展;axis默认为2,也即维度是2的shape会增大一倍。
- 但是我们也要考虑到特例,那就是如果原来的类数组a,b,c,...如果只有1或者2个维度,那么这时候,dstack函数在堆叠之前,会自动对其扩维。如果原来是一维,比如 (N,),那么扩展成 (1,N,1),如果原来是二维,比如 (M,N) ,那么扩展成(M,N,1)。
4.2 代码示例
4.3 其他情况
参考官网教程:numpy.dstack — NumPy v1.22 Manual