二叉树的遍历及其例题（数据结构学习笔记）

---

二叉树的遍历方式主要有四种：先序遍历、中序遍历、后序遍历和层次遍历。
这里我们用递归算法来讨论前三种遍历算法

先序、中序、后序遍历递归算法

1、先序遍历过程

• 访问根结点；
• 先序遍历左子树；
• 先序遍历右子树；

先序遍历算法代码

void PreOrder(BTNode *b)
{
    if(b!=NULL){
        printf("%c",b->data);
        PreOrder(b->lchild);
        PreOrder(b->rchild);
    }
}

2、中序遍历过程

• 中序遍历左子树；
• 访问根结点；
• 中序遍历右子树；

中序遍历算法代码

void InOrder(BTNode *b)
{
    if(b!=NULL){
        PreOrder(b->lchild);
        printf("%c",b->data);
        PreOrder(b->rchild);
    }
}

3、后序遍历过程

• 中序遍历左子树；
• 中序遍历右子树；
• 访问根结点；

后序遍历算法代码

void PostOrder(BTNode *b)
{
    if(b!=NULL){
        PreOrder(b->lchild);
        PreOrder(b->rchild);
        printf("%c",b->data);
    }
}

层次遍历算法

对于一颗二叉树，从根结点开始，按从上到下、从左到右的顺序访问每一个结点。
每一个结点仅仅访问一次。

算法设计思路

使用环形队列思想

1、将根节点进队
2、队不空时循环：从队列中出列一个结点*p，访问它
① 当它有左孩子结点，将左孩子结点进队。
② 当它有有孩子结点，将右孩子结点进队。

算法代码

typedef struct                  //设计队列
{
    BTNode *data[MaxSize];      //存放队中元素
    int front,rear              //队头、队尾指针
}SqQueue;                       //环形队列类型

void LevelOrder(BTNode *b)
{
    BTNode *p;
    SqQueue *qu;
    InitQueue(qu);                  //初始化队列
    enQueue(qu,b);                  //1、将根结点进队

    while(!QueueEmpty(qu)){         //队不空循环
        deQueue(qu,p);              //出队结点 p
        printf("%c",p->data);       //2、访问结点p
        if(p->lchild!=NULL)         //2.①当它有左孩子时，将左孩子进队
            enQueue(qu,p->lchild);
        if(p->rchild!=NULL)         //2.②当它有右孩子时，将右孩子进队
            enQueue(qu,p->rchild);
    }
    // 算法从根节点开始每一层都从左向右访问到，并且访问过程中也将下一层的顺序排列好了
}

算法世界复杂度为 O(n)

算法例题

例题7-11

假设二叉树采用二叉链存储结构存储，设计一个算法，计算一棵给定二叉树的所有结点个数。

算法思路

用递归遍历树求树的高度的思想去求解二叉树的所有结点个数。

• 当 b=NULL 时，f(b) = 0
• 其他情况，f(b) = f(b->lchild) + f(b->rchild) + 1

解题标程

int Nodes(BTNode *b)
{
    if(b==NULL)     //二叉树为空时，结点个数为0
        return 0;
    else            //二叉树不为空时
        return Nodes(b->lchild)+Nodes(b->rchild)+1  //递归求解左右子树的结点树，再加上根节点数1
}

例题7-12

假设二叉树采用二叉链存储结构存储，设计一个算法，输出一棵给定二叉树的所有叶子结点。

算法思路

叶子结点即该结点的左右孩子域都为空

• 当 b=NULL 时，f(b) = 不做任何事情
• 当 b 所指结点为叶子节点时，f(b) = 输出结点 b 的 data 域
• 其他情况，f(b) = f(b->lchild) ; f(b->rchild)

解题标程

void DispLeaf(BTNode *b)
{
    if(b!=NULL)
    {
        if(b->lchild==NULL&&b->rchild==NULL)    //找到结点 b 为叶子结点
            printf("%c",b->data);
        DispLeaf(b->lchild);    //递归遍历左子树寻找
        DispLeaf(b->rchild);    //递归遍历右子树寻找
    }
}

例题7-13

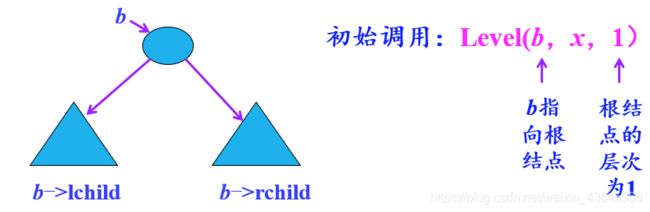
假设二叉树采用二叉链存储结构，设计一个算法 Level() 求二叉树 b 中值为 x 的结点的层次（假设所有结点值唯一）。

算法思路

设 Level(b，x，h) 返回二叉树 b 中 data 值为 x 的结点的层次，其中h 表示 b 所指结点的层数。
当在二叉树 b 中找到 data 值为 x 的结点，返回其层次（一个大于0的整数）；若没有找到，返回0。
初始调用时，b为根结点指针，h为1，即调用方式是：Level(b，x，1)。

• 当 b=NULL 时，Level(b,x,h) = 0
• 当 b 指向值为 x 的结点时，Level(b,x,h) = h,
• 其他情况：
• ① 首先在左子树中寻找，找到了直接返回 l = Level(b->lchild,x,h+1) != 0 ，Level(b,x,h) = l
• ② 否则返回在右子树中的查找结果，Level(b,x,h) = Level(b->rchild,x,h+1)

解题标程

int Level(BTNode *b,ElemType x,int h)  
//找到*p结点后h为其层次，否则为0
{
    int l;              //记录左子树中找到的 x 的层次
    if(b==NULL)         //空二叉树无结点
        return 0;
    else{
        if(b->data==x)  //找到结点 b 的 data 值为 x 
            return h;   //返回结点 b 的层次
        l=Level(b->lchild,x,h+1);   
        if(l!=0)        //找到了 x
            return l;   //返回层次l
        else            //在右子树中找，直接返回查找的值
            return Level(b->rchild,x,h+1);
    }
}
//基于先序遍历算法思想

例题7-14

假设二叉树采用二叉链存储结构，设计一个算法求二叉树b中第k层的结点个数。

算法思路

设计算法为Lnodenum(b，h，k，&n)，h表示b所指的结点层次，n是引用型参数，用于保存第k层的结点个数。
初始调用时，b为根结点指针，h为1，n赋值为0，即调用方式是：n=0；Lnodenum(b，1，k，n)。

算法设计

void Lnodenum(BTNode *b,int h,int k,int &n)
{
    if(b==NULL)         //空树直接返回
        return;
    else{               //非空树处理
        if(h==k) n++;   //当前访问的结点在第 k 层时，n 增 1
        else if(h<k){   //若当前结点层次小于 k，递归处理左、右子树
            Lnodenum(b->lchild,h+1,k,n);
            Lnodenum(b->rchild,h+1,k,n);
        }
    }
}

例题7-15

假设二叉树采用二叉链存储结构，设计一个算法判断两棵二叉树是否相似，所谓二叉树b1和b2是相似的指的是b1和b2都是空的二叉树；或者b1和b2的根结点是相似的，以及b1的左子树和b2的左子树是相似的且b1的右子树与b2的右子树是相似的。

算法思路

递归算法：

• 当 b1 = b2 = NULL，f(b1,b2) = true
• 当 b1=NULL||b2=NULL，f(b1,b2) = false
• 其他情况，f(b1,b2) = f(b1->lchild , b2->lchild) & f(b1->rchild , b2->rchild)

解题标程

bool Like(BTNode *b1，BTNode *b2)
//b1 和 b2 两棵二叉树相似时返回 true，否则返回 false
{       bool like1，like2;
        if (b1==NULL && b2==NULL)           //b1 和 b2 都是空的二叉树
	        return true;
        else if (b1==NULL || b2==NULL)      //b1 和 b2 其中一个是空的二叉树
	        return false;
        else{	                            //b1 和 b2 都不为空的二叉树
            like1=Like(b1->lchild，b2->lchild);     //递归探寻 b1的左子树 和 b2的左子树是否相似
	        like2=Like(b1->rchild，b2->rchild);     //递归探寻 b1的右子树 和 b2的右子树是否相似
	        return (like1 && like2);	    //当左右子树都相似时，才为相似树
        }
}

例题7-16

假设二叉树采用二叉链存储结构，设计一个算法输出值为x的结点的所有祖先。

算法思路

递归算法：

• 当 b=NULL，f(b,x)=false //没有祖先
• 当结点 b 左孩子或右孩子 data 域为 x， f(b,x)=true，并输出b->data
• 当 f(b->lchild , x) = true||f(b->rchild , x) = true，f(b , x)=true，并输出b->data
• 其他情况，f(b,x)=false

解题标程

bool ancestor(BTNode *b,ElemType x)
{
    if(b==NULL)             //二叉树为空时
        return false;
    else if((b->lchild!=NULL&&b->lchild==x)||   //当结点 b 左孩子或右孩子 data 域为 x
            (b->rchild!=NULL&&b->rchild==x)){  
        printf("%c",b->data);
        return true;
    }
    else if(ancestor(b->lchild,x)||ancestor(b->rchild,x)){  //当左、右子树的左孩子或右孩子 data 域为 x
        printf("%c",b->data);
        return true;
    }
    else    //其他情况
        return false;
}

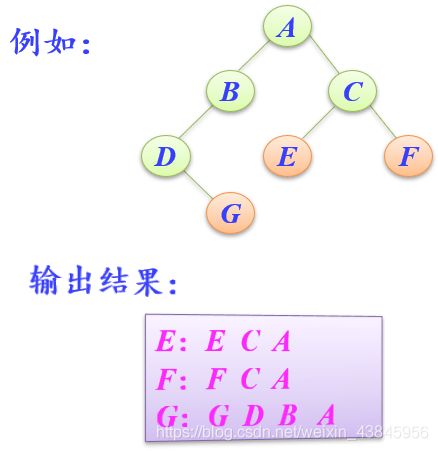
例题7-17

假设二叉树采用二叉链存储结构，设计一个算法输出从根结点到每个叶子结点的路径逆序列。
要求采用层次遍历算法来实现。

算法思路

采用类似用队列求解迷宫问题的方法。这里设计的队列为非环形队列。
当找到一个叶子结点时，在队列中通过双亲结点的位置输出根结点到该叶子结点的逆路径。

队列类型声明

typedef struct snode
{
    BTNode *pt;     //存放当前结点指针
    int parent;     //存放双亲结点在队列中的位置
}NodeType;          //非环形队列元素类型

typedef struct
{
    NodeType data[MaxSize];     //存放队列元素
    int front,rear;             //队头指针和队尾指针
}QuType;                        //顺序队类型

解题标程

void AllPath(BTNode *b)
{
    int k;
    BTNode *p;
    NodeType qelem;
    QuType *qu;         //定义非环形队列指针
    
    InitQueue(qu);                  //初始化队列
    qelem.pt=b; qelem.parent=-1;    //创建根节点对应的队列元素
    enQueue(qu,qelem);              //根节点入队

    while(!QueueEmpty(qu)){                     //队不空循环
        deQueue(qu,qelem);                      //出队元素在队中下标为qu->front
        p=qelem.pt;                             //取出元素qelem对应的结点p
        if(p->lchild==NULL&&p->rchild==NULL){   //到达叶子节点
            k=qu->front;                        //输出结点p到根结点的路径逆序列
            while (qu->data[k].parent!=-1){	    //反向输出结点直到根节点为止
                printf("%c->"，qu->data[k].pt->data);
		        k=qu->data[k].parent;
	       }
           printf("%c\n"，qu->data[k].pt->data);    //补上最后一个根节点
        }
        //层次遍历进队过程
        if (p->lchild!=NULL){		    //结点p有左孩子
            qelem.pt=p->lchild;		    //创建左孩子对应的队列元素
	        qelem.parent=qu->front; 	//其双亲位置为qu->front
	        enQueue(qu，qelem);		    //结点p的左孩子进队
        }
        if (p->rchild!=NULL){		    //结点p有右孩子  
            qelem.pt=p->rchild;		    //创建右孩子对应的队列元素
	        qelem.parent=qu->front;	    //其双亲位置为qu->front
	        enQueue(qu，qelem);		    //结点p的右孩子进队
        }
	}
}

结果图示

• 学习数据结构教程（第五版）——李春葆教授主编
• 图片来源于MOOC，数据结构——武汉大学——李春葆教授
• （如若侵权可联系QQ删除）