堆排序详解+TOP-K问题
上上篇链接: 堆的实现+堆排序_i跑跑的博客-CSDN博客
目录
分析上上篇堆排序
思路
时间空间复杂度
优化堆排序
向上调整建堆
分析
图解
时间复杂度
代码实现
向下调整建堆
分析
图解
时间复杂度
代码实现
总结
排序
思路分析
排序思想
降序建小堆证明
代码实现
小堆变大堆:
TOP-K问题
什么是TOP-K问题?
思路
时间复杂度
空间复杂度
代码实现
随机数据测试
添加排序程序
分析上上篇堆排序
上篇介绍二叉树笔记在最后实现了一个简单的堆排序:
思路
先创建一个堆,用堆堆顶的性质:选出最大或最小
用删除堆顶元素的性质:找出次大或次小
对数组进行排序
时间空间复杂度
插入和删除的时间复杂度为O(logN),最差情况下是二叉树的高度次
因为是依次插入删除,与节点个数有关,因此排序算法的时间复杂度为O(N*logN)
空间复杂度为O(N),因为要先创建一个堆,插入数组数据,大小与数组大小有关
void HeapSort(int* a,int size)
{
HP hp;
HeapInit(&hp);
//时间复杂度O(N*logN)
for (int i = 0;i优化堆排序
优化目标:时间复杂度O(N*logN)
空间复杂度O(1)
之前是先创建堆,再把数组进行插入,这次我们直接在数组里面进行建堆,令数组变成堆,使堆排序算法的空间复杂度为O(1)
在数组中有两种建堆方法:向上调整建堆
向下调整建堆
向上调整建堆
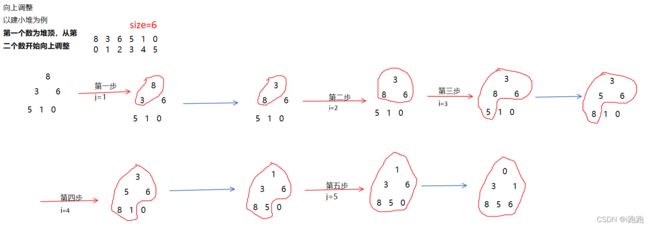
为了方便讲解,将堆向上调整在这里展示出来,以建小堆为例
分析
直接在数组中进行 size为数组元素个数
向上调整时要保证以起始节点为末尾的树必须是堆
第一个数为堆顶,从第二个数开始向上调整
从前往后,依次向上调整
图解
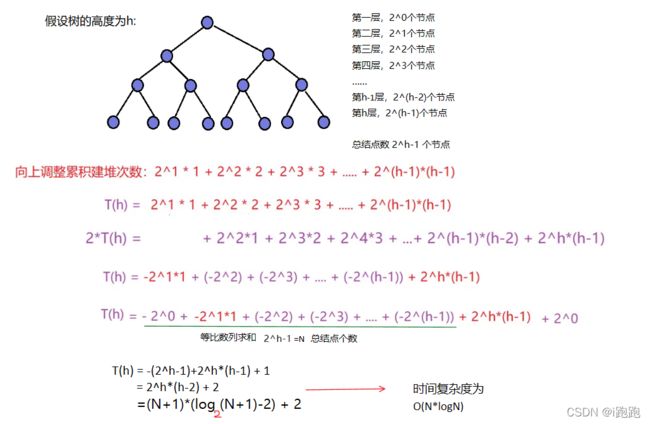
时间复杂度
代码实现
//向上调整
//建小堆为例
void Up(HPDataType* a,size_t child)
{
size_t parent = (child - 1) / 2;
while (child>0)
{
if (a[child] < a[parent])
{
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HeapSort(int* a,int size)
{
//向上调整建堆
//分析后是件复杂度为O(N*logN)
for (int i = 1;i向下调整建堆
分析
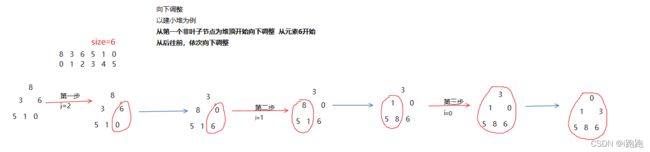
向下调整时要保证以起始节点为堆顶的树的左子树和右子树为堆
从第一个非叶子节点为堆顶开始向下调整
从后往前,依次向下调整
图解
时间复杂度
代码实现
//建小堆为例
void Down(HPDataType* a, size_t parent, size_t size)
{
size_t child = parent * 2 + 1;
while (child < size)
{
if (child + 1 =0; i--)
{
Down(a,i, size);
}
} 总结
向上调整建堆
时间复杂度为O(N*logN)向下调整建堆
时间复杂度为O(N)因此采用向下调整建堆效率更高
排序
升序建大堆
降序建小堆
思路分析
1. 注意:我们只是对数组进行向上或向下调整使它变成堆
没有创建删除堆顶元素插入、入堆等功能接口
因此HeapTop入数组和HeapPop删堆顶不能用
2. 可能有小伙伴说,那我建立这两个函数接口再使用不就行了嘛?
不可以,如果这样做,那么必然会开辟新数组将堆顶元素放入
空间复杂度变为O(N)
原本建好的堆进行堆顶与末尾的交换删除
不符合我们的优化目标
3. 那么要使空间复杂度为O(1),就必须在原数组中进行排序
排序思想
1.交换堆顶与末尾节点的元素
2.对堆前n-1个节点从堆顶开始进行向下调整
3.此时堆顶元素为最大或最小的元素
4.交换堆顶元素与第n-1个元素
5.重复上述过程,完成升序或降序
注意:末尾节点的下标更新
降序建小堆证明
升序建大堆同理分析即可。
结论:升序建大堆 降序建小堆
代码实现
先向下调整建堆(效率高)
i 为第一个非叶子节点下标
记录最后一个数据下标 end
当end=1时,结束交换和向下调整
注意:向下调整函数参数
a为数组起始地址
parent为双亲节点的下标
size为调整的元素个数
void Down(HPDataType* a, size_t parent, size_t size);下面代码中要注意end代表的含义
while前代表最后一个元素下标
while中代表的是要调整的元素个数
void HeapSort(int* a,int size) { //升序建大堆 //降序建小堆 for (int i = (size-1-1)/2; i>=0; i--) { Down(a,i, size); } //最后一个数据的下标 size_t end = size - 1; while (end>0) { swap(&a[0],&a[end]); Down(a,0,end); end--; } }
这样堆排序就可以实现啦
决定升序还是降序,创建大堆或小堆即可
小堆变大堆:
改变建堆时的大于小于号即可
child和child+1、child和parent的比较符号
TOP-K问题
什么是TOP-K问题?
即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序
如果数据量非常大(几十个G),排序就不太可取了,内存会非常大,效率极低
最佳的方式就是用堆排序来解决
思路
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较小堆时,比堆顶大的元素替换堆顶
向下调整,保证堆的结构
大堆时,比堆顶小的元素替换堆顶
向下调整,保证堆的结构
依次比较完后,堆里面就是所有数据中最大或最小的前K个元素
只需要遍历一次即可
时间复杂度
建立堆为K,最坏情况下剩余的N-K个数都要进行调整
调整次数为logK*(N-K)次
O(K+logK*(N-K))
K大小不确定,不能省略
空间复杂度
只需要开辟K个空间来建堆
O(K)
代码实现
//TOP-K问题
void PrintTopK(int* a, int n, int k)
{
// 1. 建堆--用a中前k个元素建堆
int* kHeap = (int*)malloc(sizeof(int)*k);
if (kHeap == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//将前k个数插入数组kHeap中
for (int i = 0;i= 0; i--)
{
Down(a, i, k);
}
// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
for (int i = k;ikHeap[0])
{
kHeap[0] = a[i];
Down(kHeap,0,k);
}
}
// 3. 打印最大或最小的前k个
for (int j = 0;j 随机数据测试
生成100000以内的随机数,将10个100000内的随机位置变成比100000大的数
找出10000个数中最大的十个数
运行代码
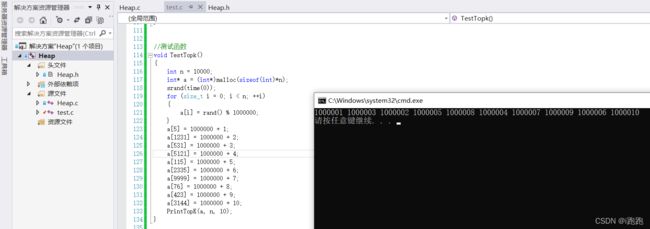
void TestTopk() { int n = 10000; int* a = (int*)malloc(sizeof(int)*n); srand(time(0)); for (size_t i = 0; i < n; ++i) { a[i] = rand() % 1000000; } a[5] = 1000000 + 1; a[1231] = 1000000 + 2; a[531] = 1000000 + 3; a[5121] = 1000000 + 4; a[115] = 1000000 + 5; a[2335] = 1000000 + 6; a[9999] = 1000000 + 7; a[76] = 1000000 + 8; a[423] = 1000000 + 9; a[3144] = 1000000 + 10; PrintTopK(a, n, 10); } int main() { TestTopk(); return 0; }运行结果:
可以得到最大的10个数,但他们是无序的
添加排序程序
//TOP-K问题
void PrintTopK(int* a, int n, int k)
{
// 1. 建堆--用a中前k个元素建堆
int* kHeap = (int*)malloc(sizeof(int)*k);
if (kHeap == NULL)
{
printf("malloc fail\n");
exit(-1);
}
//将前k个数插入数组kHeap中
for (int i = 0;i= 0; i--)
{
Down(a, i, k);
}
// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
for (int i = k;ikHeap[0])
{
kHeap[0] = a[i];
Down(kHeap,0,k);
}
}
// 3. 排序
//最后一个数据的下标
size_t end = k - 1;
while (end>0)
{
swap(&kHeap[0], &kHeap[end]);
Down(kHeap, 0, end);
end--;
}
// 4. 打印排序后的前k个
for (int j = 0;j 运行结果
堆排序和TOP-K问题的笔记到这里就结束啦,欢迎各位伙伴在留言区里交流评价噢,求赞求赞求赞!!!