全变分图像去噪算法（TV）

全变分图像去噪算法（Total varivation）

今天一起学习一下全变分图像去噪算法，与之前的高斯、均值滤波等各向同性模型不同，全变分模型是一个依靠梯度下降法对图像进行平滑的各向异性的模型，希望在图像内部尽可能对图像进行平滑（相邻像素的差值较小），而在图像边缘（图像轮廓）尽可能不去平滑。想要全面了解全变分模型，需要知道泛函分析，梯度下降法，欧拉拉格朗日方程E-L等概念。
最早于1992年，Rudin, Osher和Fatemi提出了经典的全变差图像去噪算法，原文：Nonlinear total variation based noise removal algorithms。
与以往的去噪/滤波算法不同，TV算法是一种图像复原算法，它是将干净的图像从噪声图像中复原出来，通过建立噪声模型，采用最优化算法求解模块，并通过不断迭代的过程，使得复原出的图像无限逼近理想去噪后的图像。与深度学习十分类似，噪声模型类比于损失函数，通过不断训练，使得两者的差距越来越接近，同样需要梯度下降法快速得到最优解。
传统的图像去噪方法都是建立在线性系统的基础上运用反卷积的方法来复原图像，但这类方法通常会平滑边缘信息，而图像的固有特征是存在突变(如边缘)的，若以L2范数作为“平滑性”的量度，则会出现对大的梯度的“惩罚”，这与图像的固有特征是相斥的。基于这一考虑，Rudin, Osher 和 Fatemi 首先提出以
L1范数的梯度（导数）作为图像平滑性的度量，由此开创了一种新的图像去噪方法——TV 去噪方法。TV 去噪方法优点是允许出现尖锐的不连续点，这点对于图像去噪问题尤其重要，如边缘轮廓或运动的边界，这些边缘都代表重要的特征，采用此方法可以很好的保护边缘。但 TV 方法会产生阶梯效应，即平滑区域转换成分段常数区域，且会丢掉纹理等细节特征。

参考论文：《图像去噪的 ROF 模型的理论分析与算法研究》主要介绍三种去除不同噪声的模型：
下面是对ROF模型进行求解：

具体求解过程可以看详细算法参见：
全变分（TV）模型原理与C++实现
经典全变分图像去噪算法（tv算法）公式推导与MATLAB实现
MATLAB代码，主函数：

close all
clear
clc

%% 参数设置
% 迭代次数
IterMax = 15;
% 松弛因子 必须大于0(拉格朗日乘数)
lambda = 0.03;  
imageName = 'lena512.bmp';

%% 读图
srcImage = imread(imageName);
srcImage = im2double(srcImage);

%% 添加高斯噪声
image_noise = imnoise(srcImage, 'gaussian', 0, 0.01);

%% TV算法
dstImage = total_variation(image_noise,IterMax,lambda);

%% 图像显示
figure;
subplot(1,2,1);imagesc(image_noise);axis image; axis off; colormap(gray);title('噪声图像');   
subplot(1,2,2);imagesc(dstImage);axis image; axis off; colormap(gray);title('全变差去噪图像'); 

%% 图像评价指标
PSNR = psnr(srcImage,dstImage);
SSIM = ssim(srcImage,dstImage);

TV算法实现：

function u=total_variation(u0,IterMax,lambda)
%% 初始化
u=u0;
[M,N]=size(u);  
Energy(IterMax) = 0;
% 空间离散
h=1;

%% 迭代
for Iter=1:IterMax    
    
    for i=2:M-1       
        for j=2:N-1
            % 系数计算
            ux=(u(i+1,j)-u(i,j))/h;
            uy=(u(i,j+1)-u(i,j-1))/2*h;
            Grad=sqrt(ux*ux+uy*uy);
            % 梯度为0 co1->Inf 可能导致图像变黑
            if Grad ~=0  
                co1=1./Grad; 
            else
                co1 = Grad;
            end
            
            ux=(u(i,j)-u(i-1,j))/h;
            uy=(u(i-1,j+1)-u(i-1,j-1))/2*h;
            Grad=sqrt(ux*ux+uy*uy);
            if Grad ~=0  
                co2=1./Grad; 
            else
                co2 = Grad;
            end
            
            ux=(u(i+1,j)-u(i-1,j))/2*h;
            uy=(u(i,j+1)-u(i,j))/h;
            Grad=sqrt(ux*ux+uy*uy);
            if Grad ~=0 
                co3=1./Grad; 
            else
                co3 = Grad;
            end
            
            ux=(u(i+1,j-1)-u(i-1,j-1))/2*h;
            uy=(u(i,j)-u(i,j-1))/h;
            Grad=sqrt(ux*ux+uy*uy);
            if Grad ~=0 
                co4=1./Grad; 
            else
                co4 = Grad;
            end
            u(i,j)=(u0(i,j)+(1/lambda*h*h)*(co1*u(i+1,j)
            +co2*u(i-1,j)+co3*u(i,j+1)+co4*u(i,j-1)))
            *(1/(1+(1/(lambda*h*h)*(co1+co2+co3+co4))));     
        end
    end
    % 边缘条件
    for i=2:M-1
        u(i,1)=u(i,2);    % 第一列的计算等于第二列
        u(i,N)=u(i,N-1);  % 最后一列的计算等于倒数第二列
    end
    
    for j=2:N-1   
        u(1,j)=u(2,j);
        u(M,j)=u(M-1,j);  % 同理，第一行和最后一行的计算等于和它相近的行
    end
    
    u(1,1)=u(2,2);
    u(1,N)=u(2,N-1);
    u(M,1)=u(M-1,2);
    u(M,N)=u(M-1,N-1);    % 四个角的值也近似与它相近的点
    
    % 计算每次迭代的离散能量
    en=0.0;   % 设能量初始值为0
    for i=2:M-1
        for j=2:N-1
            ux=(u(i+1,j)-u(i,j))/h;
            uy=(u(i,j+1)-u(i,j))/h;
            fid=(u0(i,j)-u(i,j))*(u0(i,j)-u(i,j));
            en=en+sqrt(ux*ux+uy*uy)+lambda*fid;
        end
    end
    % 计算每次迭代的能量
    Energy(Iter)=en;
end

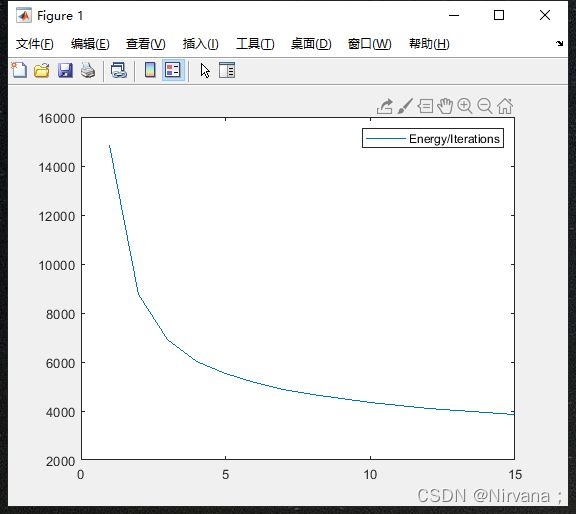
%% 绘图-每次迭代的能量
figure
plot(Energy);legend('Energy/Iterations');

效果图如下：