- 作者:韩信子@ShowMeAI
- 教程地址:http://www.showmeai.tech/tutorials/35
- 本文地址:http://www.showmeai.tech/article-detail/224
- 声明:版权所有,转载请联系平台与作者并注明出处
收藏ShowMeAI查看更多精彩内容
本系列为吴恩达老师《深度学习专项课程(Deep Learning Specialization)》学习与总结整理所得,对应的课程视频可以在这里查看。
引言
在ShowMeAI前一篇文章 CNN应用:目标检测 中我们对以下内容进行了介绍:
- 目标定位
- 特征点检测
- 目标检测
- 边框预测
- 非极大值抑制
- YOLO
- RCNN
本篇主要介绍计算机视觉中其他应用,包括人脸识别和神经风格迁移。
1.人脸识别
我们本节要介绍到人脸的一些计算机视觉应用,首先我们对人脸验证(Face Verification)和人脸识别(Face Recognition)做一个区分:
- 人脸验证:一般指一个一对一问题,只需要验证输入的人脸图像是否与某个已知的身份信息对应。
- 人脸识别:一个更为复杂的一对多问题,需要验证输入的人脸图像是否与多个已知身份信息中的某一个匹配。
上面2个任务中,一般人脸识别比人脸验证更难一些。因为假设人脸验证系统的错误率是1%,那么在人脸识别中,输出分别与K个模板都进行比较,则相应的错误率就会增加,约K%。模板个数越多,错误率越大。
1.1 One-Shot 学习
人脸识别所面临的一个挑战是要求系统只采集某人的一个面部样本,就能快速准确地识别出这个人,即只用一个训练样本来获得准确的预测结果。这被称为One-Shot学习。
One-shot learning对于数据库中的\( N\) 个人,对于每张输入图像,Softmax输出\( N+1\) 种标签(N个人+都不是=N+1种类别),这种处理方法有两个缺点:
- 每个人只有一张图片,训练样本少,构建的CNN网络不够健壮。
- 若数据库增加另一个人,输出层Softmax的维度就要发生变化,相当于要重新构建CNN网络,使模型计算量大大增加,不够灵活。
为了解决One-shot学习的问题,引入了相似函数(similarity function)。相似函数表示两张图片的相似程度,用\( d(img1,img2)\) 来表示。若\( d(img1,img2)\) 较小,则表示两张图片相似,是同一个人;若\( d(img1,img2)\) 较大,则表示两张图片不是同一个人。
相似函数定义及判定规则如下:
$$ Similarity = d(img1, img2) $$
- \( d(img1,img2)\leq \tau\) 则判定图片相似
- \( d(img1,img2)> \tau\) 则判定图片不同
具体的,在人脸识别问题中,会计算测试图片与数据库中\( K\) 个目标的相似函数,取其中\( d(img1,img2)\) 最小的目标为匹配对象。若所有的\( d(img1,img2)\) 都很大,则表示数据库没有这个人。
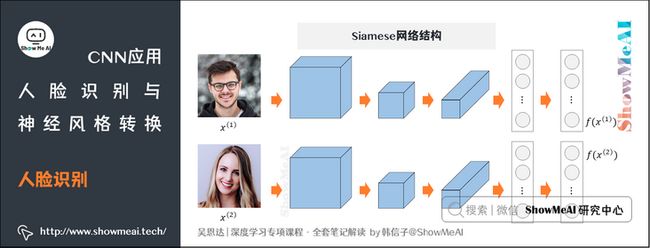
1.2 Siamese 网络
我们在前面的内容里,看到CNN对于图像有很好的表征能力,训练好的模型可以通过网络层次计算对图像做非常有效的向量化表征,基于此基础我们可以构建图像相似度度量学习的网络,这就是著名的Siamese 网络,它是一种对两个不同输入运行相同的卷积网络,然后对它们的结果进行比较的神经网络。
Siamese网络的大致结构如下:
上图中2张图片\( x^{(1)}\) 、\( x^{(2)}\) 分别输入两个相同的卷积网络中,经过全连接层后不再进行Softmax,而是得到特征向量\( f(x^{(1)})\) 、\( f(x^{(2)})\) 。
这时,可以通过各自网络层的输出向量之差的范数来表示两幅图片的差异度:
$$ d(x^{(1)}, x^{(2)}) = ||f(x^{(1)}) - f(x^{(2)})||^2_2 $$
注意到,在Siamese网络中,不同图片使用的是同一套CNN网络结构和参数。我们会训练网络,不断调整网络参数,使得属于同一人的图片之间\( d(x^{(1)},x^{(2)})\) 很小,而不同人的图片之间\( d(x^{(1)},x^{(2)})\) 很大。最终:
- 若\( x^{(i)}\) 、\( x^{(j)}\) 是同一个人,则\( ||f(x^{(1)})-f(x^{(2)})||^2\) 较小
- 若\( x^{(i)}\) 、\( x^{(j)}\) 不是同一个人,则\( ||f(x^{(1)})-f(x^{(2)})||^2\) 较大
相关论文:Taigman et al., 2014, DeepFace closing the gap to human level performance
1.3 Triplet 损失
回到人脸识别的任务,要构建出合适的CNN模型,我们需要引入Triplet Loss这个损失函数。
Triplet Loss需要每个样本包含三张图片:靶目标(Anchor)、正例(Positive)、反例(Negative),所以它也译作「三元组损失」。
如图所示,靶目标和正例是同一人,靶目标和反例不是同一人。Anchor和Positive组成一类样本,Anchor和Negative组成另外一类样本。
我们希望前面提到的Siamese网络中的CNN输出图像表征\( f(A)\) 接近\( f(D)\) ,即\( ||f(A)-f(D)||^2\) 尽可能小,而\( ||f(A)-f(N)||^2\) 尽可能大,数学上满足:
$$ ||f(A)-f(P)||^2\leq ||f(A)-F(N)||^2 $$
$$ ||f(A)-f(P)||^2-||f(A)-F(N)||^2\leq 0 $$
上述不等式约束有个问题:如果所有的图片都是零向量,即\( f(A)=0,f(P)=0,f(N)=0\) ,那么上述不等式也满足。但是这对我们进行人脸识别没有任何作用。
我们希望得到\( ||f(A)-f(P)||^2\) 远小于\( ||f(A)-F(N)||^2\) 。所以,我们添加一个超参数\( \alpha\) ,且\( \alpha>0\) ,对不等式约束修改如下:
$$ ||f(A)-f(P)||^2-||f(A)-F(N)||^2\leq -\alpha $$
$$ ||f(A)-f(P)||^2-||f(A)-F(N)||^2+\alpha \leq 0 $$
不等式中的\( \alpha\) 也被称为边界margin,和支持向量机中的margin类似(详细算法可以参考ShowMeAI文章 SVM模型详解)。举个例子,若\( d(A,P)=0.5\) ,\( \alpha=0.2\) ,则\( d(A,N)\geq0.7\) 。
接下来,基于A,P,N三张图片,就可以定义Loss function为:
$$ L(A,P,N)=max(||f(A)-f(P)||^2-||f(A)-F(N)||^2+\alpha,\ 0) $$
那么对于m组训练样本的数据集,我们的cost function为:
$$ J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)}) $$
关于训练样本,必须保证同一人包含多张照片,否则无法使用这种方法。例如10k张照片包含1k个不同的人脸,则平均一个人包含10张照片。这个训练样本是满足要求的。
数据准备完毕之后,就可以使用梯度下降算法,不断训练优化CNN网络参数,让我们数据集上的cost function不断减小接近0。
一些训练细节:
① 同一组训练样本,A,P,N的选择尽可能不要使用随机选取方法。
- 因为随机选择的A与P一般比较接近,A与N相差也较大,毕竟是两个不同人脸。
- 这样的话,也许模型不需要经过复杂训练就能实现这种明显识别,但是抓不住关键区别。
② 最好的做法是人为选择A与P相差较大(例如换发型,留胡须等),A与N相差较小(例如发型一致,肤色一致等)。
- 这种人为地增加难度和混淆度会让模型本身去寻找学习不同人脸之间关键的差异,「尽力」让\( d(A,P)\) 更小,让\( d(A,N)\) 更大,即让模型性能更好。
如下为一些A、P、N的例子:
相关论文:Schroff et al., 2015, FaceNet: A unified embedding for face recognition and clustering
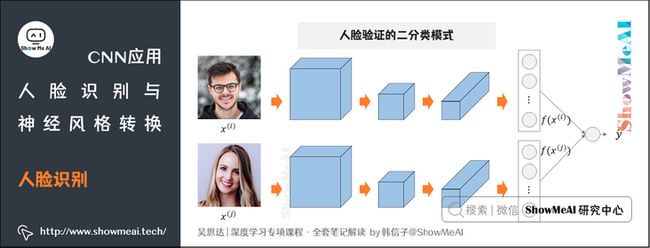
1.4 人脸验证与二分类模式
除了Triplet损失函数,二分类结构也可用于学习参数以解决人脸识别问题。其做法是输入一对图片,将两个Siamese网络产生的特征向量输入至同一个Sigmoid单元,输出1则表示是识别为同一人,输出0则表示识别为不同的人。
在上述网络中,每个训练样本包含两张图片。通过Siamese网络把人脸识别问题转化成了一个二分类问题。引入逻辑输出层参数\( w\) 和\( b\) ,输出\( \hat y\) 表达式为:
$$ \hat y=\sigma(\sum_{k=1}^Kw_k|f(x^{(i)})_k-f(x^{(j)})_k|+b) $$
其中参数\( w_k\) 和\( b\) 都是通过梯度下降算法迭代训练得到。
\( \hat y\) 的另外一种表达式为:
$$ \hat y=\sigma(\sum_{k=1}^Kw_k\frac{(f(x^{(i)})_k-f(x^{(j)})_k)^2}{f(x^{(i)})_k+f(x^{(j)})_k}+b) $$
上式被称为\( \chi\) 方公式,也叫\( \chi\) 方相似度。
训练好上述模型后,进行人脸识别的常规方法是测试图片与模板分别进行网络计算,编码层输出比较,计算二分类概率结果。
为了减少计算量,可以提前进行预计算:提前将数据库每个模板的编码层输出\( f(x)\) 保存下来。这个过程可以并行,而且因为是离线过程,对于时效性要求并没有那么高。
实际测试预估时,库内的人脸编码都已计算好,只需要计算测试图片的网络输出,得到的\( f(x^{(i)})\) 直接与存储的模板\( f(x^{(j)})\) 进行下一步的计算即可,总计算时间减小了接近一半。
这种方法也可以应用在之前提到的triplet loss网络中。
2.神经风格迁移
神经风格迁移(Neural style transfer)将参考风格图像的风格「迁移」到另外一张内容图像中,生成具有其特色的图像。如下是几个神经风格迁移的例子:
后续的方法介绍和推导中:我们会用\( C\) 表示内容图片,\( S\) 表示风格图片,\( G\) 表示生成的图片。
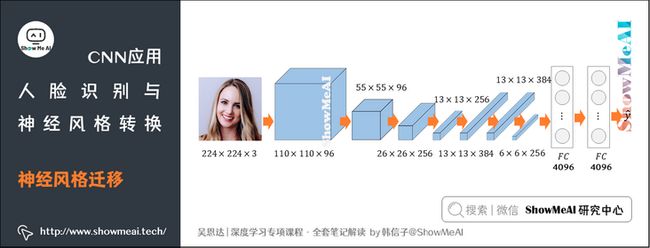
2.1 深度卷积网络学到了什么
想要理解如何实现神经风格转换,首先要理解在输入图像数据后,一个深度卷积网络从中都学到了些什么。我们借助可视化来做到这一点。
典型的CNN网络结构如下:
我们从第1个隐层开始可视化解释,我们遍历所有训练样本,找出让该层激活函数输出最大的9块图像区域;然后再找出该层的其它单元(不同的滤波器通道)激活函数输出最大的9块图像区域;最后共找\( 9\) 次,得到\( 9 \times 9\) 的图像如下所示,其中每个\( 3 \times 3\) 区域表示一个运算单元。
上图表明,第1层隐层检测的是原始图像的边缘和颜色阴影等简单信息。用同样的方法去操作CNN的后续隐层,随着层数的增加,捕捉的区域更大,特征逐步变得复杂,从边缘到纹理再到具体物体。
相关论文:Zeiler and Fergus., 2013, Visualizing and understanding convolutional networks
2.2 代价函数
神经风格迁移生成图片G的代价函数由两部分组成:\( C\) 与\( G\) 的内容相似程度和\( S\) 与\( G\) 的风格相似程度。其中,\( \alpha\) 、\( \beta\) 是超参数,用来调整相对比重。
神经风格迁移的算法步骤如下所示:
- 随机生成图片\( G\) 的所有像素点。
- 使用梯度下降算法使代价函数最小化,以不断修正\( G\) 的所有像素点,使G逐渐有C的内容和G的风格。
相关论文:Gatys al., 2015. A neural algorithm of artistic style
(1) 内容代价函数
上述代价函数包含一个内容代价部分和风格代价部分。我们先看内容代价函数\( J_{content}(C, G)\) ,它表示图片\( C\) 和图片\( G\) 之间的内容相似度。我们一般基于一个中间层\( l\) 层的激活函数输出 \( a^{(C)[l]}\) 与 \( a^{(G)[l]}\) 来衡量\( C\) 和\( G\) 之间的内容相似度。
具体的\( J_{content}(C, G)\) 计算过程如下:
- 使用一个预训练好的CNN(例如VGG);
- 选择一个隐藏层\( l\) 来计算内容代价。\( l\) 太小则内容图片和生成图片像素级别相似,\( l\) 太大则可能只有具体物体级别的相似。因此,\( l\) 一般选一个中间层;
- 设\( a^{(C)[l]}\) 、\( a^{(G)[l]}\) 为\( C\) 和\( G\) 在\( l\) 层的激活,则有:
$$ J_{content}(C, G) = \frac{1}{2}||(a^{(C)[l]} - a^{(G)[l]})||^2 $$
\( a^{(C)[l]}\) 和\( a^{(G)[l]}\) 越相似,则\( J_{content}(C, G)\) 越小。
(2) 风格代价函数
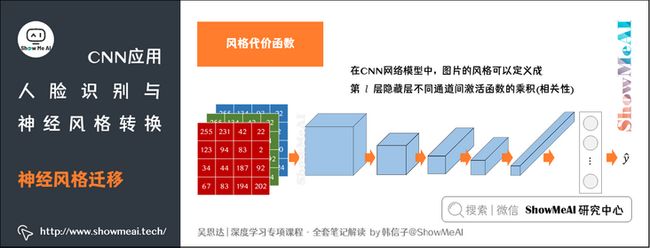
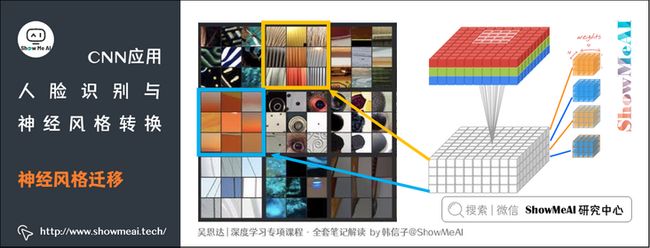
接下来我们要讨论风格代价函数,在CNN网络模型中,图片的风格可以定义成第l层隐藏层不同通道间激活函数的乘积(相关性)。
每个通道提取图片的特征不同,如下图:
- 标为黄色的通道提取的是图片的垂直纹理特征,标为蓝色的通道提取的是图片的背景特征(橙色)。
- 计算这两个通道的相关性,相关性的大小,即表示原始图片既包含了垂直纹理也包含了该橙色背景的可能性大小。
- 通过CNN,「风格」被定义为同一个隐藏层不同通道之间激活值的相关系数,因其反映了原始图片特征间的相互关系。
对于风格图像\( S\) ,选定网络中的第\( l\) 层,我们定义图片的风格矩阵(style matrix)为:
$$ G^{[l](S)}_{kk\prime} = \sum^{n^{[l]}_H}_{i=1} \sum^{n^{[l]}_W}_{j=1} a^{[l](S)}_{ijk} a^{[l](S)}_{ijk\prime} $$
其中,\( i\) 和\( j\) 为第\( l\) 层的高度和宽度;\( k\) 和\( k\prime\) 为选定的通道,其范围为\( 1\) 到\( n_C^{[l]}\) ;\( a^{l}_{ijk}\) 为激活。
同理,对于生成图像\( G\) ,有:
$$ G^{[l](G)}_{kk\prime} = \sum^{n^{[l]}_H}_{i=1} \sum^{n^{[l]}_W}_{j=1} a^{[l](G)}_{ijk} a^{[l](G)}_{ijk\prime} $$
因此,第\( l\) 层的风格代价函数为:
$$ J^{[l]}_{style}(S, G) = \frac{1}{(2n^{[l]}_Hn^{[l]}_Wn^{[l]}_C)^2} \sum_k \sum_{k\prime}(G^{[l](S)}_{kk\prime} - G^{[l](G)}_{kk\prime})^2 $$
上面我们只计算了一层隐层l的代价函数。使用多隐层可以表征的风格更全面,我们对其叠加,最终表达式为:
$$ J_{style}(S, G) = \sum_l \lambda^{[l]} J^{[l]}_{style}(S, G) $$
公式中,\( \lambda\) 是用于设置不同层所占权重的超参数。
2.3 推广至一维和三维
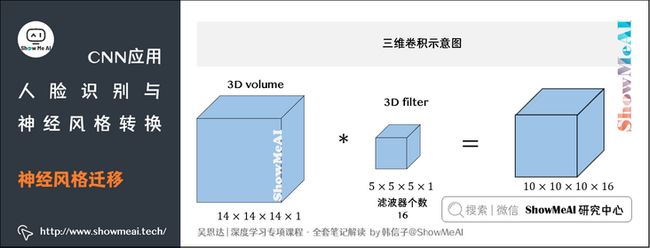
前面我们处理的都是二维图片,举例来说:
- 输入图片维度:\( 14 \times 14 \times 3\)
- 滤波器尺寸:\( 5 \times 5 \times 3\) ,滤波器个数:\( 16\)
- 输出图片维度:\( 10 \times 10 \times 16\)
实际上卷积也可以延伸到一维和三维数据。我们来举例说明:
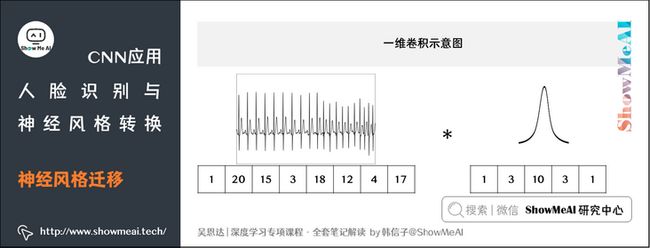
(1) 一维卷积(1D Conv)
EKG数据(心电图)是由时间序列对应的每个瞬间的电压组成,是一维数据。如果用卷积处理,有如下结果:
- 输入时间序列维度:\( 14 \times 1\)
- 滤波器尺寸:\( 5 \times 1\) ,滤波器个数:\( 16\)
- 输出时间序列维度:\( 10 \times 16\)
(2) 三维卷积(3D Conv)
而对于三维图片的示例,对应的3D卷积有如下结果:
- 输入3D图片维度:\( 14 \times 14 \times 14 \times 1\)
- 滤波器尺寸:\( 5 \times 5 \times 5 \times 1\) ,滤波器个数:\( 16\)
- 输出3D图片维度:\( 10 \times 10 \times 10 \times 16\)
参考资料
- Taigman et al., 2014, DeepFace closing the gap to human level performance
- Schroff et al., 2015, FaceNet: A unified embedding for face recognition and clustering
- Zeiler and Fergus., 2013, Visualizing and understanding convolutional networks
- Gatys al., 2015. A neural algorithm of artistic style
ShowMeAI系列教程推荐
- 图解Python编程:从入门到精通系列教程
- 图解数据分析:从入门到精通系列教程
- 图解AI数学基础:从入门到精通系列教程
- 图解大数据技术:从入门到精通系列教程
- 图解机器学习算法:从入门到精通系列教程
- 机器学习实战:手把手教你玩转机器学习系列
- 深度学习教程 | 吴恩达专项课程 · 全套笔记解读
推荐文章
- 深度学习教程 | 深度学习概论
- 深度学习教程 | 神经网络基础
- 深度学习教程 | 浅层神经网络
- 深度学习教程 | 深层神经网络
- 深度学习教程 | 深度学习的实用层面
- 深度学习教程 | 神经网络优化算法
- 深度学习教程 | 网络优化:超参数调优、正则化、批归一化和程序框架
- 深度学习教程 | AI应用实践策略(上)
- 深度学习教程 | AI应用实践策略(下)
- 深度学习教程 | 卷积神经网络解读
- 深度学习教程 | 经典CNN网络实例详解
- 深度学习教程 | CNN应用:目标检测
- 深度学习教程 | CNN应用:人脸识别和神经风格转换
- 深度学习教程 | 序列模型与RNN网络
- 深度学习教程 | 自然语言处理与词嵌入
- 深度学习教程 | Seq2seq序列模型和注意力机制