算法学习-最短路Dijkstra算法
文章目录
-
- 概念介绍
-
- 最短路问题
- Dijkstra算法
- 实现步骤
- 算法复杂度分析
- 代码实现
-
- 最短路代码
- 最短路图的创建
- 路径回溯
- 调用示例
概念介绍
本博客在学习北京大学陈斌老师《数据结构与算法》MOOC课程中总结反思形成。
最短路问题
- 带权图上最短路径的问题
- 词梯问题的高阶形式(可以认为词梯问题是权重都一致的最短路问题)
Dijkstra算法
- 一个迭代算法,得出从一个顶点到其余所有顶点的最短路径
实现步骤
准备阶段
- 在顶点Vertex类中的成员dist用于记录从开始顶点到本顶点的最短带权路径长度(权重之和)
- 顶点的访问次序由一个优先队列来控制,队列中作为优先级的是顶点的dist属性。
实现阶段
- 只有开始顶点dist设为0,而其他所有顶点dist设为sys.maxsize(最大整数),全部加入优先队列;
- 随着队列中每个最低dist顶点率先出队,并计算它与邻接顶点的权重,会引起其它顶点dist的减小和修改,引起堆重排;
- 并据更新后的dist优先级再依次出队。
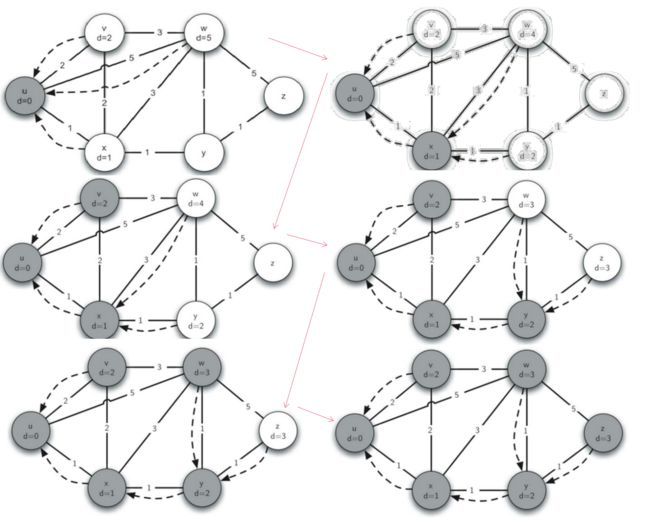
可视化
算法复杂度分析
- 所有顶点加入优先队列并且建堆,时间复杂度 O ( ∣ V ∣ ) O(|V|) O(∣V∣);
- 每个顶点仅出队1次,每次delMin花费 O ( l o g ∣ V ∣ ) O(log|V|) O(log∣V∣),一共是 O ( ∣ V ∣ l o g ∣ V ∣ ) O(|V|log|V|) O(∣V∣log∣V∣);
- 每个边关联到的顶点做一次decreaseKey操作( O ( l o g ∣ V ∣ ) O(log|V|) O(log∣V∣)),一共是 O ( ∣ E ∣ l o g ∣ V ∣ ) O(|E|log|V|) O(∣E∣log∣V∣);
- 综上所述:数量级是 O ( ( ∣ V ∣ + ∣ E ∣ ) l o g ∣ V ∣ ) O((|V|+|E|)log|V|) O((∣V∣+∣E∣)log∣V∣)。
代码实现
最短路代码
陈斌老师实现的最短路算法
def dijkstra(aGraph, start):
pq = PriorityQueue()
start.setDistance(0)
# 对所有顶点建堆,形成优先队列
pq.buildHeap([(v.getDistance(), v) for v in aGraph])
while not pq.isEmpty():
# 优先队列出队
currentVert = pq.delMin()
for nextVert in currentVert.getConnections():
newDist = currentVert.getDistance() + currentVert.getWeight(nextVert)
if newDist < nextVert.getDistance():
# 修改出队顶点所邻接顶点的distm并逐个重拍队列
nextVert.setDistance(newDist)
nextVert.setPred(currentVert)
pq.decreaseKey(nextVert, newDist)
自己为调用该算法实现的图的创建和路径回溯
最短路图的创建
这里为了方便以后的调用,考虑到邻接矩阵使用的广泛性,实现了给定邻接矩阵,创建邻接表图
# 实现邻接矩阵转化为邻接图
def Matrix2Graph(LJGraph, LJmatrix):
for i in range(len(LJmatrix)):
LJGraph.addVertex(i)
for i in range(len(LJmatrix)):
for j in range(len(LJmatrix[0])):
if i != j:
LJGraph.addEdge(i, j, LJmatrix[i][j])
# 检验构造的图的正确性
for v in LJGraph:
for w in v.getConnections():
print("%s,%s" % (v.getId(), w.getId()))
print(v.getWeight(w))
路径回溯
在Dijkstra算法求解出最短路后,回溯出终点到起点的最短路径
def traverse(y):
x = y
_temp = []
_temp.append(x.getId())
while (x.getPred()):
_temp.append(x.getPred().getId())
x = x.getPred()
return _temp
调用示例
if __name__ == '__main__':
LJGraph = Graph()
LJmatrix = [[0, 2, 5, 1, sys.maxsize, sys.maxsize],
[2, 0, 3, 2, sys.maxsize, sys.maxsize],
[5, 3, 0, 3, 1, 5],
[1, 2, 3, 0, 1, sys.maxsize],
[sys.maxsize, sys.maxsize, 1, 1, 0, 1],
[sys.maxsize, sys.maxsize, 5, sys.maxsize, 1, 0]]
# 复习:对于基础的二维列表,利用len获取形状
# print(LJmatrix)
# print(LJmatrix[0][1])
Matrix2Graph(LJGraph, LJmatrix)
# 如何使用Dijkstra(迪杰斯特拉算法)算法
dijkstra(LJGraph, LJGraph.getVertex(0))
# 如何反向调用得到图的解
path = traverse(LJGraph.getVertex(5))
print(path)
dijkstra(LJGraph, LJGraph.getVertex(0))
# 如何反向调用得到图的解
path = traverse(LJGraph.getVertex(5))
print(path)