单源最短路奇技淫巧之迪杰斯特拉算法(Dijkstra)
单源最短路之迪杰斯特拉算法(Dijkstra)
问题定义:
求解单源点的最短路径问题:给定带权有向图G和源点s,求点s到图G中其他点的最短路径
可以采用迪杰斯特拉算法(Dijkstra),或者SPFA算法,这里我先介绍一下第一种Dijksta算法
核心思想:
其核心思想就是贪心o(︶︿︶)o(我怎么感觉好多算法基本上不是大暴力就是大贪心)
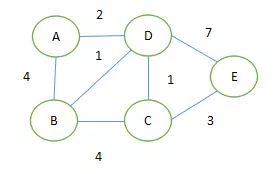
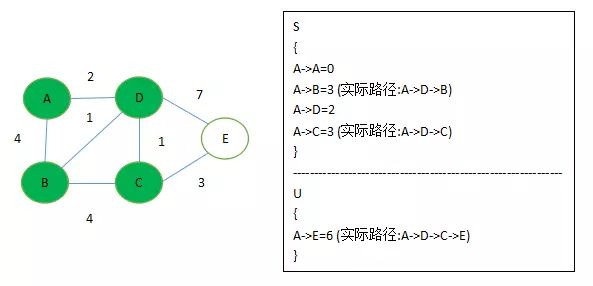
1、指定一个节点,例如我们要计算 ‘A’ 到其他节点的最短路径
2、引入两个集合(S、U),S集合包含已求出的最短路径的点(以及相应的最短长度),U集合包含未求出最短路径的点(以及A到该点的路径,注意 如上图所示,A->C由于没有直接相连 初始时为∞)
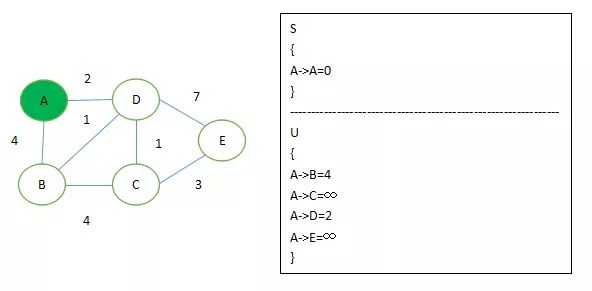
3、初始化两个集合,S集合初始时 只有当前要计算的节点,A->A = 0,
U集合初始时为 A->B = 4, A->C = ∞, A->D = 2, A->E = ∞
ps: 直接连接的定义长度,其他认为不可达。
接下来要进行核心两步骤了
4、从U集合中找出路径最短的点,加入S集合,例如 A->D = 2
ps: 这里就是一个核心的排序流程,选择最近的一个点加入集合。
5、更新U集合路径,if ( ‘D 到 B,C,E 的距离’ + ‘AD 距离’ < ‘A 到 B,C,E 的距离’ ) 则更新U
ps: 如果通过新的路径可以让距离变得更短,就更新集合 U 信息。
6、循环执行 4、5 两步骤,直至遍历结束,得到A 到其他节点的最短路径
算法图解:
1、选定A节点并初始化,如上述步骤3所示
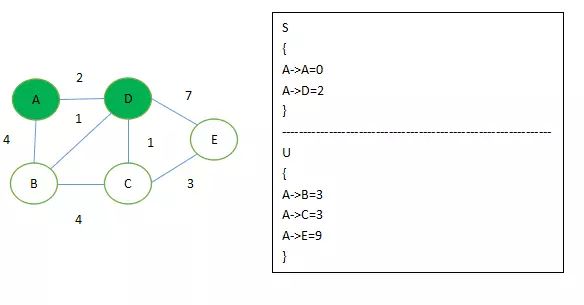
2、执行上述 4、5两步骤,找出U集合中路径最短的节点D 加入S集合,并根据条件 if ( ‘D 到 B,C,E 的距离’ + ‘AD 距离’ < ‘A 到 B,C,E 的距离’ ) 来更新U集合
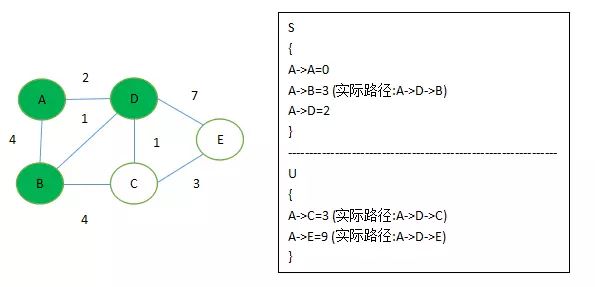
3、这时候 A->B, A->C 都为3,没关系。其实这时候他俩都是最短距离,如果从算法逻辑来讲的话,会先取到B点。
而这个时候 if 条件变成了 if ( ‘B 到 C,E 的距离’ + ‘AB 距离’ < ‘A 到 C,E 的距离’ ) ,如图所示这时候A->B距离,其实为 A->D->B
4、思路就是这样,往后就是大同小异了
5、算法结束
松弛操作
- 假如存在一条从u 到 v的边,其长度为w(u,v)那么从s 到 v到一条新路径就是 s -> u -> v,这条新路径的长度就是dist[u] + w(u, v),如果dist[u] + w(u, v) < 原来的dist[v],就可以对其进行松弛操作,修改dist[v] = dist[u] + w(u, v),一直这样子搞下去(>_<)
思考
该算法的时间复杂度是 O ( n 2 ) O(n^2) O(n2),主要花在了U集合中寻找最短路径上,所以我们可以用一个堆来维护最小值,将取出最短路径的复杂度降为 O ( 1 ) O(1) O(1),每次调整的复杂度降为O(elogn),e为该点的边数,所以复杂度降为O((m+n)logn)。
使用通过优先队列来维护
解题步骤为:
- 初始化
- 存图
- 进行dijkstra算法
- 输出结果
边的存储:
采用链式前向星!
首先我们需要一个结构体:
struct ran{
int to, next, val;
}tr[MAX];
和一个数组:
int head[MAX];
和一个代表边的下标的变量:
int tot = 0;
其中head存的是起点,结构体存每条边的后继节点,next“指针”和边的权值
建图的代码如下:
void built(int u, int v, int c){
tr[++tot].to = v;//第tot条边的后继节点为v
tr[tot].val = c;//第tot条边的权值为c
tr[tot].next = head[u];//存将上一个前继节点为u的边的下标
head[u] = tot;//更新头节点的值
}
边的遍历:
遍历以x为前继节点的所有边时,只需要这样:
for(int i = head[now.to]; i != -1; i = tr[i].next)
记得赋初值为-1
Dijkstra代码的实现:
P3371 【模板】单源最短路径(弱化版)
结构体版
#include
#includepari版
#include
#include