深度学习教程 | AI应用实践策略(上)
- 作者:韩信子@ShowMeAI
- 教程地址:http://www.showmeai.tech/tutorials/35
- 本文地址:http://www.showmeai.tech/article-detail/219
- 声明:版权所有,转载请联系平台与作者并注明出处
收藏ShowMeAI查看更多精彩内容
本系列为吴恩达老师《深度学习专项课程(Deep Learning Specialization)》学习与总结整理所得,对应的课程视频可以在这里查看。
引言
在ShowMeAI前一篇文章网络优化:超参数调优、正则化、批归一化和程序框架中我们对以下内容进行了介绍:
- 超参数优先级与调参技巧
- 超参数的合适范围确定
- Batch Normalization
- softmax回归
- 深度学习框架
本篇 和 下篇 主要对吴恩达老师第3门课《Structuring Machine Learning Projects》(构建机器学习项目)相关内容做总结梳理。内容主要覆盖机器学习中的一些策略和方法,让我们能够更快更有效地让机器学习系统工作。
对于一个已经被构建好且产生初步结果的机器学习系统,为了能使结果更令人满意,往往还要进行大量的改进。之前的内容部分介绍了很多改进的方法,包括:
- 收集更多数据
- 调试超参数
- 调整神经网络的大小或结构
- 采用不同的优化算法
- 添加正则化
可选择的方法很多,也很复杂、繁琐。盲目选择、尝试不仅耗费时间而且可能收效甚微。想要找准改进的方向,使一个机器学习系统更快更有效地工作,就需要学习一些在构建机器学习系统时常用到的策略。
1.正交化
机器学习中有许多参数、超参数需要调试。通过每次只调试一个参数,保持其它参数不变,而得到的模型某一性能改变是一种最常用的调参策略,我们称之为正交化方法(Orthogonalization)。
正交化的核心在于每次调整只会影响模型某一方面的性能,而对其他功能没有影响。这种方法有助于更快更有效地进行机器学习模型的调试和优化。
在机器学习(监督学习)系统中,我们希望模型有4重评价:
- 建立的模型在训练集上表现良好
- 建立的模型在验证集上表现良好
- 建立的模型在测试集上表现良好
- 建立的模型在实际应用中表现良好
其中:
- 对于第①条,如果模型在训练集上表现不好,可以尝试训练更复杂的神经网络或者换一种更好的优化算法(例如Adam)。
- 对于第②条,如果模型在验证集上表现不好,可以进行正则化处理或者加入更多训练数据。
- 对于第③条,如果模型在测试集上表现不好,可以尝试使用更大的验证集进行验证。
- 对于第④条,如果模型在实际应用中表现不好,可能是因为测试集没有设置正确或者成本函数评估指标有误,需要改变测试集或成本函数。
每一种“功能”对应不同的调节方法。而这些调节方法(旋钮)只会对应一个“功能”,是正交的。面对遇到的各种问题,正交化能够帮助我们更为精准有效地解决问题。
在模型功能调试中并不推荐使用早停法early stopping。如果早期停止,虽然可以改善验证集的拟合表现,但是对训练集的拟合就不太好。因为对两个不同的“功能”都有影响,所以早停止法不具有正交化。虽然也可以使用,但是用其他正交化控制手段来进行优化会更简单有效。
2.单值评价指标
(关于本节涉及到的机器学习应用中的评估指标详解,推荐阅读ShowMeAI文章 图解机器学习 | 模型评估方法与准则)
构建与优化机器学习系统时,单值评价指标非常必要。通过设置一个量化的单值评价指标(single-number evaluation metric),可以使我们根据这一指标比较不同超参数对应的模型的优劣,从而选择最优的那个模型。
例如,对于二分类问题,常用的评价指标是精确率(Precision)和召回率(Recall)。
假设我们有A和B两个分类器,其两项指标分别如图。但实际应用中,我们通常使用综合了精确率和召回率的单值评价指标 F 1 − S c o r e F1-Score F1−Score 来评价模型的好坏。 F 1 − S c o r e F1- Score F1−Score 其实就是精准率和召回率的调和平均数(Harmonic Mean),比单纯的平均数效果要好。我们计算出两个分类器的F1-Score,对比会发现A模型的效果要更好。
除了F1-Score之外,我们还可以使用平均值作为单值评价指标来对模型进行评估。
如图所示, A A A、 B B B、 C C C、 D D D、 E E E、 F F F六个模型对不同国家样本的错误率不同,可以计算其平均性能,然后选择平均错误率最小的那个模型( C C C模型)。
3.优化指标和满足指标
有时候,要把所有的性能指标都综合在一起,构成单值评价指标是比较困难的(比如在上面例子的基础上加入模型效率即运行时间)。这时,我们可以将某些指标作为优化指标(Optimizing Metric),寻求它们的最优值;而将某些指标作为满足指标(Satisficing Metric),只要在一定阈值以内即可。
我们以猫类识别的分类器为例,有A、B、C三个模型,各个模型的Accuracy和**运行时间(Running time)**如下表中所示:
我们可以将Accuracy作为优化指标(Optimizing metic),将Running time作为满足指标(Satisficing metic):给Running time设定一个阈值,在其满足阈值的情况下,选择Accuracy最大的模型。
如上例中设定Running time必须在100ms以内:
- 模型C不满足阈值条件,首先剔除
- 模型B相比较模型A而言,Accuracy更高,性能更好
总结一下:优化指标(Optimizing metic)是需要优化的,越优越好,满足指标(Satisficing metic)只要满足设定的阈值就好了。上例中,准确率就是优化指标,因为我们想要分类器尽可能做到正确分类;而运行时间就是一个满足指标,如果你想要分类器的运行时间不多于某个阈值,那最终选择的分类器就应该是以这个阈值为界里面准确率最高的那个。
4.动态改变评价指标
对于模型的评价标准优势需要根据实际情况进行动态调整,以让模型在实际应用中获得更好的效果。
例如,有时我们不太能接受某些分类错误,于是改变单纯用错误率作为评价标准,给某些分类错误更高的权重,以从追求最小错误率转为追求最小风险。
5.训练 / 验证 / 测试集划分
ShowMeAI在前面的文章 深度学习的实用层面 中提到了,我们会将数据集分为训练集、验证集、测试集。构建机器学习系统时,我们采用不同的学习方法,在训练集上训练出不同的模型,然后使用验证集对模型的好坏进行评估,确信其中某个模型足够好时再用测试集对其进行测试。
训练集、验证集、测试集的设置对于机器学习模型非常重要,合理的设置能够大大提高模型训练效率和模型质量。
5.1 验证集和测试集的分布
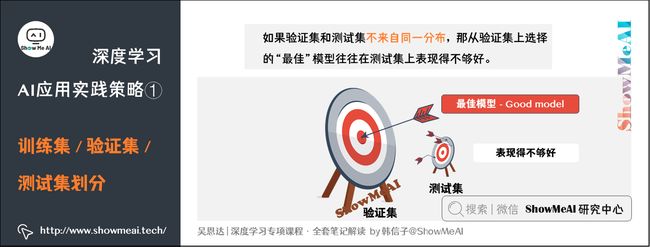
验证集和测试集的数据来源应该相同(来自同一分布)、和机器学习系统将要在实际应用中面对的数据一致,且必须从所有数据中随机抽取。这样,系统才能做到尽可能不偏离目标。
如果验证集和测试集不来自同一分布,那么我们从验证集上选择的“最佳”模型往往不能够在测试集上表现得很好。这就好比我们在验证集上找到最接近一个靶的靶心的箭,但是我们测试集提供的靶心却远远偏离验证集上的靶心,结果这支肯定无法射中测试集上的靶心位置。
5.2 验证集和测试集的大小
过去数据量较小(小于1万)时,通常将数据集按照以下比例进行划分,以保证验证集和测试集有足够的数据:
- 无验证集的情况:70% / 30%;
- 有验证集的情况:60% / 20% / 20%;
现在的机器学习时代数据集规模普遍较大,例如100万数据量,这时将相应比例设为 98% / 1% / 1% 或 99% / 1% 就已经能保证验证集和测试集的规模足够。
5.3 何时改变开发/验证集和评价指标
算法模型的评价标准有时候需要根据实际情况进行动态调整,目的是让算法模型在实际应用中有更好的效果。
依旧以猫类识别的分类器为例。初始的评价标准是错误率,算法A错误率为3%,算法B错误率为5%,从错误率评价指标上看显然A更好一些。但是,实际使用时发现算法A会通过一些色情图片,但是B没有出现这种情况。从用户的角度来说,他们可能更倾向选择B模型,虽然B的错误率高一些。
这时候,我们就需要改变之前单纯只是使用错误率作为评价标准,而考虑新的情况进行改变。例如增加色情图片的权重,增加其代价。
原来的cost function:
J = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J=\frac1m\sum_{i=1}^mL(\hat y^{(i)},y^{(i)}) J=m1i=1∑mL(y^(i),y(i))
更改评价标准后的cost function:
J = 1 w ( i ) ∑ i = 1 m w ( i ) L ( y ^ ( i ) , y ( i ) ) J=\frac{1}{w^{(i)}}\sum_{i=1}^mw^{(i)}L(\hat y^{(i)},y^{(i)}) J=w(i)1i=1∑mw(i)L(y^(i),y(i))
w ( i ) = { 1 , x ( i ) i s n o n − p o r n 10 , x ( i ) i s p o r n w^{(i)}= \begin{cases} 1, & x^{(i)}\ is\ non-porn\\ 10, & x^{(i)}\ is\ porn \end{cases} w(i)={1,10,x(i) is non−pornx(i) is porn
综上,总体来说机器学习可分为两个过程:① 定义一个合适的评价指标,② 基于上述指标评估当前模型的表现。也就是说,第1步是找靶心,第2步是通过训练,射中靶心。但是在训练的过程中可能会根据实际情况改变算法模型的评价标准,进行动态调整。
还有一种情况下,我们需要动态改变评价标准:我们的验证集/测试集与实际使用的样本分布不一致。比如猫类识别分类场景下样本图像分辨率差异。
6.比较人类表现水平
很多机器学习模型的诞生是为了取代人类的工作,因此其表现也会跟人类表现水平作比较。下图展示了随着时间的推进,机器学习系统和人的表现水平的变化。
一般的,当机器学习超过人的表现水平后,它的进步速度逐渐变得缓慢,最终性能无法超过某个理论上限,这个上限被称为贝叶斯最优误差(Bayes Optimal Error)。
贝叶斯最优误差一般认为是理论上可能达到的最优误差。换句话说,其就是理论最优函数,任何从 x x x 到精确度 y y y 映射的函数都不可能超过这个值。例如,对于语音识别,某些音频片段嘈杂到基本不可能知道说的是什么,所以完美的识别率不可能达到100%。
因为人类对于一些自然感知问题的表现水平十分接近贝叶斯最优误差,所以当机器学习系统的表现超过人类后,就没有太多继续改善的空间了。而当构建的机器学习模型的表现还没达到人类的表现水平时,我们会使用各种方式来提升它:
- 采用人工标记过的数据进行训练
- 通过人工误差分析了解为什么人能够正确识别
- 进行偏差、方差分析
当模型的表现超过人类后,这些方法的作用就微乎其微了。
6.1 可避免偏差
实际应用中,要看人类表现(误差),训练误差和验证误差的相对值。以猫类识别分类为例:
- 如果人类误差为1%,模型训练误差为8%,验证误差为10%。由于前两者相差7%,后两者之间只相差2%,所以目标是尽量在训练过程中减小训练误差,即减小偏差bias。
- 如果图片很模糊,肉眼也看不太清,人类表现(误差)提高到7.5%。此时,由于训练误差与其只相差0.5%,验证误差与训练误差相差2%,所以目标是尽量在训练过程中减小验证误差,即方差variance。
所以这个过程,我们看的更多是相对的数据。
模型在「训练集上的误差」与「人类表现水平」的差值被称作可避免偏差(Avoidable Bias)。
可避免偏差低便意味着模型在训练集上的表现很好,而训练集与验证集之间错误率的差值越小,意味着模型在验证集与测试集上的表现和训练集同样好。
如果可避免偏差大于训练集与验证集之间错误率的差值,之后的工作就应该专注于减小偏差;反之,就应该专注于减小方差。
6.2 理解人类表现水平
我们说了很多时候会用**人类水平误差(Human-level Error)**来代表贝叶斯最优误差(或者简称贝叶斯误差)。对于不同领域的例子,不同人群由于其经验水平不一,错误率也不同。**一般来说,我们将表现最好的作为人类水平误差。**但是实际应用中,不同人选择人类水平误差的基准是不同的,这会带来一定的影响。
吴恩达老师的课程里,以医疗影像场景举例说明了,这个场景下不同人群的识别error有所不同:
- 普通大众人群:3%错误率
- 普通医生:1%错误率
- 有经验的医生:0.7%错误率
- 有经验的医生团队:0.5%错误率
上例中不同人群的错误率不同。一般来说,我们将表现最好的那一组,即「有经验的医生团队」作为「人类水平」,即human-level error就为0.5%。但是实际应用中,不同人可能选择的「人类水平」基准是不同的,这对我们后续会带来一些影响。
假如该模型训练误差为0.7%,验证为0.8%
- 如果选择「有经验的医生团队」,即人类水平误差为0.5%,则此时bias比variance更加突出。
- 如果选择「有经验的医生」,即人类水平误差为0.7%,则variance更加突出。
大家可以看到,选择什么样的人类水平误差,有时候会影响bias和variance值的相对变化。当然这种情况一般只会在模型表现很好,接近bayes optimal error的时候出现。越接近bayes optimal error,模型越难继续优化,因为这时候的人类水平误差可能是比较模糊难以准确定义的。
7.超越人类的表现
对于自然感知类问题,例如视觉、听觉等,机器学习的表现暂时还不及人类。但是在很多其它方面,机器学习模型的表现已经超过人类了,包括:
- 在线广告(计算广告)
- 商品推荐
- 物流时间预估等
- 贷款申请审批
机器学习模型超过人类水平是比较困难的。但是只要提供足够多的样本数据,训练复杂的神经网络,模型预测准确性会大大提高,很有可能接近甚至超过人类水平。而当算法模型的表现超过人类水平时,很难再通过人的直觉来解决如何继续提高算法模型性能的问题
8.总结
提高机器学习模型性能主要要解决两个问题:avoidable bias和variance。训练误差与人类水平误差之间的差值反映的是avoidable bias,验证误差与训练误差之间的差值反映的是variance。
基本假设
- 模型在训练集上有很好的表现
- 模型推广到开发和测试集啥也有很好的表现
8.1 减少可避免偏差(avoidable bias)
当我们发现模型的主要问题是「可避免偏差」时,我们可以采用如下方式优化:
- 训练更大的模型
- 训练更长时间、训练更好的优化算法(Momentum、RMSprop、Adam)
- 寻找更好的网络架构(RNN、CNN)、寻找更好的超参数
8.2 减少方差(variance)
当我们发现模型的主要问题是「方差」时,我们可以采用如下方式优化:
- 收集更多的数据
- 正则化(L2、dropout、数据增强)
- 寻找更好的网络架构(RNN、CNN)、寻找更好的超参数
参考资料
- 图解机器学习 | 模型评估方法与准则
ShowMeAI系列教程推荐
- 图解Python编程:从入门到精通系列教程
- 图解数据分析:从入门到精通系列教程
- 图解AI数学基础:从入门到精通系列教程
- 图解大数据技术:从入门到精通系列教程
- 图解机器学习算法:从入门到精通系列教程
- 机器学习实战:手把手教你玩转机器学习系列
- 深度学习教程 | 吴恩达专项课程 · 全套笔记解读
推荐文章
- 深度学习教程 | 深度学习概论
- 深度学习教程 | 神经网络基础
- 深度学习教程 | 浅层神经网络
- 深度学习教程 | 深层神经网络
- 深度学习教程 | 深度学习的实用层面
- 深度学习教程 | 神经网络优化算法
- 深度学习教程 | 网络优化:超参数调优、正则化、批归一化和程序框架
- 深度学习教程 | AI应用实践策略(上)
- 深度学习教程 | AI应用实践策略(下)
- 深度学习教程 | 卷积神经网络解读
- 深度学习教程 | 经典CNN网络实例详解
- 深度学习教程 | CNN应用:目标检测
- 深度学习教程 | CNN应用:人脸识别和神经风格转换
- 深度学习教程 | 序列模型与RNN网络
- 深度学习教程 | 自然语言处理与词嵌入
- 深度学习教程 | Seq2seq序列模型和注意力机制