NLP-transformer-预备知识(self-Attention)
NLP-transformer-预备知识(self-Attention)
- 一、自注意力机制在 transformer 中的应用
- 二、self-Attention 引出
- 三、self-Attention 单步计算过程
- 四、self-Attention 向量计算过程
- 五、多头自注意力机制 计算过程
- 六、self-Attention 需要配合位置信息
一、自注意力机制在 transformer 中的应用
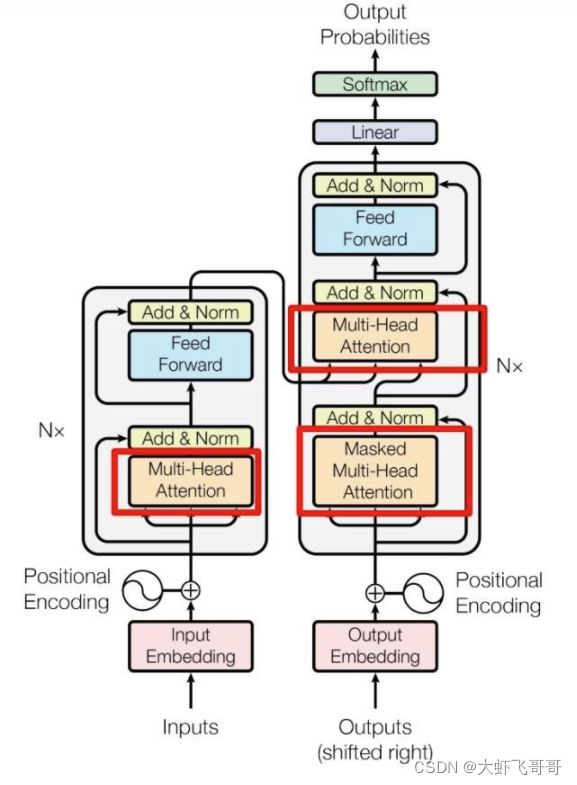
下图是Transformer 的内部结构图,左侧为 Encoder block,右侧为 Decoder block。红色圈中的部分为 Multi-Head Attention,是由多个 Self-Attention组成的,可以看到 Encoder block 包含一个 Multi-Head Attention,而 Decoder block 包含两个 Multi-Head Attention。
二、self-Attention 引出
以词性标注为例, 对于下图中,单词 “saw” 有两种不同的词性。

当尝试用全链接作为训练模型,输入为单词的词向量时。很显然 ,输入相同的词向量只能输出相同的词性,因为模型没有考虑前后文的联系。
一种解决方法:选择适当的窗口,把当前输入的上下文也当作训练数据,一起训练。

存在什么问题呢?
1、当想要考虑整个句子的语境,就需要把窗口设置为整个句子的长度。
2、预料中,句子的长度不一致,就需要统计所有句子,选择最长的句子的长度作为窗口。
3、当句子选择最长的,训练费时,容易产生过拟合。
神经网络接收的输入是很多大小不一的向量,并且不同向量向量之间有一定的关系,但是实际训练的时候无法充分发挥这些输入之间的关系而导致模型训练结果效果极差。
针对这些问题,通过引入 self-Attention 来解决,self-Attention 实际上是想让机器注意到整个输入中不同部分之间的相关性。
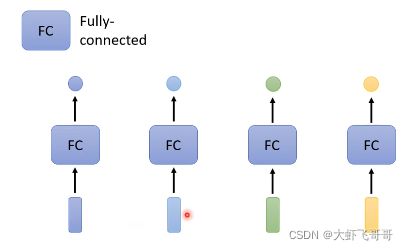
在全连接中使用 self-Attention,整体结构如下图,两者交替使用,self-Attention 处理整个句子的信息, FC 专注处理某个位置的信息。self-Attention 可以作为输入层或者隐藏层,
三、self-Attention 单步计算过程
分部拆解: 首先, 要分别计算第一个输入 a 1 a^1 a1 和其他输入 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4 的相关性。
相关性(α)计算方法:具体方式如下,transformer 中使用的第一种方式。

计算流程如下: 使用第一个输入 a 1 a^1 a1 的 q 1 q^1 q1(查询向量)和 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4 的 k i k^i ki 矩阵分别相乘得到 a 1 a^1 a1 和 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4 之间的相关性值 α 1 i α_{1i} α1i。
接下来,进行 softmax 运算,此过程不一定使用 softmax, 也可以使用 RELU 等其他函数计算。
提取句子中重要信息: 根据上述计算的相关性 α 1 i α_{1i} α1i, 依次和 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4 的 v i v^i vi 向量相乘,把得到的结果相加得到 b 1 b^1 b1。 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4 与 a 1 a^1 a1 相关性越高,对应提取 v i v^i vi 的信息越多。
假设 a 1 a^1 a1 和 a 2 a^2 a2 最相关, v 2 v^2 v2 抽取的信息越多, 得到的 b 1 b^1 b1 更关注 v 2 v^2 v2 的信息。
四、self-Attention 向量计算过程
上述多个输入可以以矩阵的形式并行运算,具体计算过程如下:
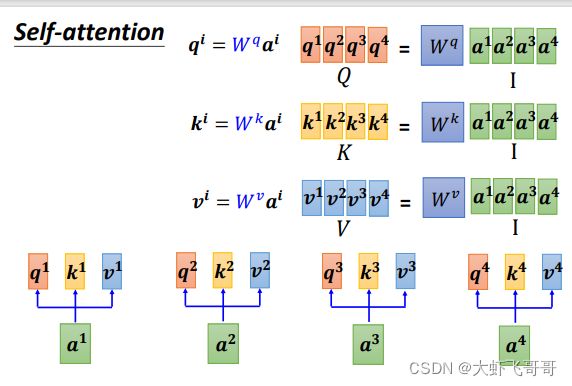
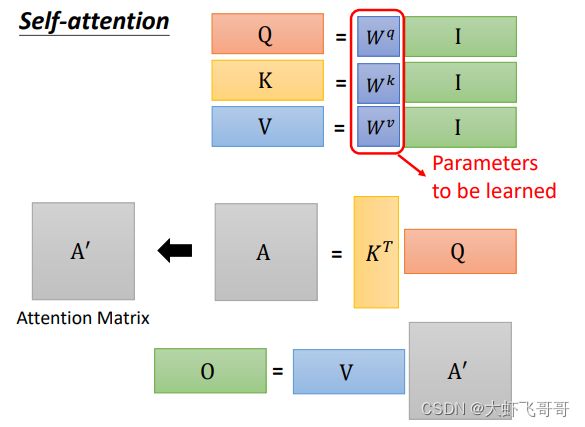
第一步: 对于每一个向量 a a a,分别乘上三个系数矩阵 W q W^q Wq, W k W^k Wk, W v W^v Wv得到 Q Q Q, K K K, V V V三个值, 分别表示 Query, Key 和 Value。
向量形式: Q = W q ∗ I Q = W^q * I Q=Wq∗I、 K = W k ∗ I K = W^k * I K=Wk∗I、 V = W v ∗ I V = W^v * I V=Wv∗I
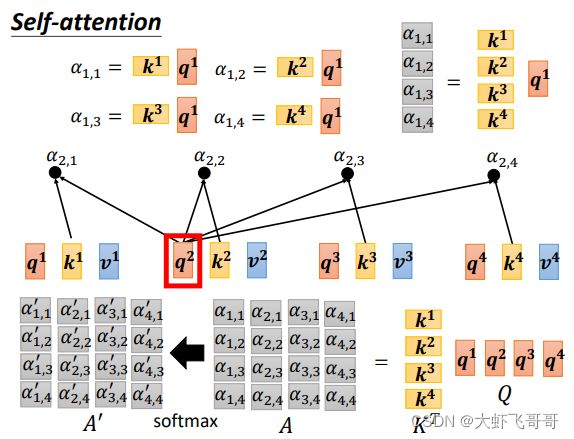
第二步: 利用得到的 Q Q Q 和 K K K 计算每两个输入向量之间的相关性,也就是计算 Attention 的值 α α α, 然后对 α α α 进行softmax 操作。
α i j = ( q i ) T ⋅ k j α_{ij} = (q^i)^T · k^j αij=(qi)T⋅kj
向量形式: A = K T ⋅ Q A = K^T · Q A=KT⋅Q
softmax: A ′ = s o f t m a x ( A ) A^{'}= softmax(A) A′=softmax(A)
第三步: 利用得到的 A ′ A' A′ 和 V V V 计算每个输入向量 a a a 对应的 self-attention 层的输出向量 b b b.
b i = ∑ j = 1 n v i ∗ α i j ′ b_i = \sum_{j=1}^{n} v_i * {\alpha }'_{ij} bi=∑j=1nvi∗αij′
向量形式: O = V ⋅ A ′ O = V · A' O=V⋅A′

总结: 最终需要训练的参数为 W q W^q Wq、 W k W^k Wk、 W v W^v Wv
五、多头自注意力机制 计算过程
自注意力机制还有一个进阶版,叫多头自注意力机制(multi-head self-attention)。多个自注意力机制并行运算,得到的结果拼接,经过线性层输出。

为什么要多头呢?
自注意力机制实质上是用 q q q 向量去找相关的 k k k 向量,但是相关性可能有多种,一个 q q q 只能找到一种相关的 k k k 向量,因此就要引入多个 q q q 向量和向量 k k k 来捕捉多种相关性。
多头注意力机制具体计算流程如下:
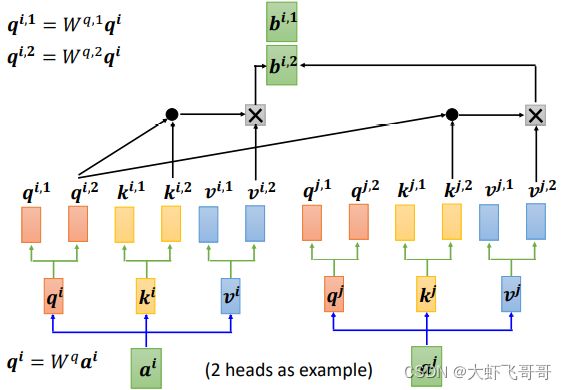
在得到不同的输出 O i O^i Oi 后,再将其拼到一起,形成一个大的矩阵。如果是 2 头,就将这 2 个输出直接拼到一起。然后通过一个转换矩阵 W o W^o Wo 将拼接的矩阵转换成原输出的长度的向量。

六、self-Attention 需要配合位置信息
自注意力机制虽然考虑了所有的输入向量,但没有考虑到向量的位置信息。在实际的文字处理问题中,可能在不同位置词语具有不同的性质,比如动词往往较低频率出现在句首。
有学者提出可以通过位置编码(Positional Encoding)来解决这个问题:对每一个输入向量加上一个位置向量e,位置向量的生成方式有多种,通过e来表示位置信息,代入self-attention层进行计算。