2018蓝桥杯省赛Java B组 回忆录
下周就是第十届蓝桥杯省赛了,才发现,原来距离去年参赛已经快一年了。去年由于自己的大意马虎,做了一回“送财童子”,这不,今年打算重新找回场子来了。 那就让我从今天开始,好好的刷一下真题,来巩固下算法吧。
下面先来回忆下去年的蓝桥杯赛事吧。第九届蓝桥杯,在愚人节这一天,没错,就是这个奇妙的日子,被代码玩弄了一天,好吧,我承认还是因为我太菜了。
第一题:第几天
2000年的1月1日,是那一年的第1天。 那么,2000年的5月4日,是那一年的第几天?注意:需要提交的是一个整数,不要填写任何多余内容。
哈哈哈,这题就太简单了,直接脑算就行了啊,点开计算机右下角时间,把1月到5月的时间相加就行 了啊
第二题:方格记数
如图p1.png所示,在二维平面上有无数个1x1的小方格。我们以某个小方格的一个顶点为圆心画一个半径为1000的圆。 你能计算出这个圆里有多少个完整的小方格吗?
注意:需要提交的是一个整数,不要填写任何多余内容。
这道题的思路,现在想起来,真的是好简单哦。因为是圆,所以只需要考虑第一象限就行,只要别忘了在最后把所求结果×4就行。首先,我们从原点开始考虑,设坐标点为(i,j),我们只需要考虑此时小方格的右上角顶点仍在圆内就行,即此时(i+1)(i+1)+(j+1)(j+1)<=1000000即可,遍历0—1000内所有符合要求的点。代码如下:
public class Main {
public static void main(String[] args) {
int R=1000;
int a=1000,b=0,tb=b,count=0;
for(a=1000;a>=0;a--) {
while(a*a+b*b<=R*R)b++;
b--;
count+=a*(b-tb);
tb=b;
}
System.out.println(count*4); //答案 3137548
}
}
第三题:复数幂
设i为虚数单位。对于任意正整数n,(2+3i)^n 的实部和虚部都是整数。 求 (2+3i)^123456 等于多少?
即(2+3i)的123456次幂,这个数字很大,要求精确表示。答案写成 "实部±虚部i"
的形式,实部和虚部都是整数(不能用科学计数法表示),中间任何地方都不加空格,实部为正时前面不加正号。(2+3i)^2 写成: -5+12i,
(2+3i)^5 的写成: 122-597i注意:需要提交的是一个很庞大的复数,不要填写任何多余内容。
这个就很好办了,把实部和虚部存储,然后乘以123456次就行,不过在这里千万不能出错哦,因为123456的次方是一个极大数,所以这里需要用到long。答案为:13483137+1100011648i
代码示例如下:
public class Main {
public static void main(String[] args) {
int a = 2, b = 3;
for(int i = 2; i<=123456; i++){
int temp = 2*a-3*b;
b = 3*a+2*b;
a = temp;
}
System.out.println(a+"+"+b+"i");
}
}第四题:测试次数
x星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。
各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通。x星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的2楼。
如果手机从第7层扔下去没摔坏,但第8层摔坏了,则手机耐摔指数=7。 特别地,如果手机从第1层扔下去就坏了,则耐摔指数=0。
如果到了塔的最高层第n层扔没摔坏,则耐摔指数=n为了减少测试次数,从每个厂家抽样3部手机参加测试。
某次测试的塔高为1000层,如果我们总是采用最佳策略,在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?
请填写这个最多测试次数。
注意:需要填写的是一个整数,不要填写任何多余内容。
这一题,当初比赛的时候做错了,以为用二分法就可以了,但忘记了题目的要求是3部手机,所以这里用深度搜索来解决。
①从第100层开始,每次层数增加100,直至手机摔碎,则最多会有10次
②从①中摔碎层的往下数90层开始,每次增加10层,最多有9次
③从个位数层数开始,则会有9次可能性
所以综上得最多会有28次可能性
第五题:快速排序
以下代码可以从数组a[]中找出第k小的元素。它使用了类似快速排序中的分治算法,期望时间复杂度是O(N)的。
请仔细阅读分析源码,填写划线部分缺失的内容。
注意:只提交划线部分缺少的代码,不要抄写任何已经存在的代码或符号。
import java.util.Random;
public class Main{
public static int quickSelect(int a[], int l, int r, int k) {
Random rand = new Random();
int p = rand.nextInt(r - l + 1) + l;
int x = a[p];
int tmp = a[p]; a[p] = a[r]; a[r] = tmp;
int i = l, j = r;
while(i < j) {
while(i < j && a[i] < x) i++;
if(i < j) {
a[j] = a[i];
j--;
}
while(i < j && a[j] > x) j--;
if(i < j) {
a[i] = a[j];
i++;
}
}
a[i] = x;
p = i;
if(i - l + 1 == k) return a[i];
if(i - l + 1 < k) return quickSelect( _________________________________ ); //填空
else return quickSelect(a, l, i - 1, k);
}
public static void main(String args[]) {
int [] a = {1, 4, 2, 8, 5, 7};
System.out.println(quickSelect(a, 0, 5, 4));
}
}
一个分治法进行快速排序 分治法三步
1.将问题分成尽量左右相等的左右两半
2.递归求解左右两半
3.合并左右两半问题和当前问题比较 熟悉的话一眼看出,这个也简单
答案:a,l,i+1,k
第六题:递增三元组
给定三个整数数组 A = [A1, A2, ... AN], B = [B1, B2, ... BN], C = [C1, C2,
... CN], 请你统计有多少个三元组(i, j, k) 满足:
- 1 <= i, j, k <= N
- Ai < Bj < Ck
【输入格式】 第一行包含一个整数N。 第二行包含N个整数A1, A2, ... AN。 第三行包含N个整数B1, B2, ... BN。
第四行包含N个整数C1, C2, ... CN。对于30%的数据,1 <= N <= 100
对于60%的数据,1 <= N <= 1000
对于100%的数据,1 <= N <=
100000 0 <= Ai, Bi, Ci <= 100000【输出格式】 一个整数表示答案
【输入样例】
3
1 1 1
2 2 2
3 3 3【输出样例】
27资源约定: 峰值内存消耗(含虚拟机) < 256M CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。 所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
不要使用package语句。不要使用jdk1.7及以上版本的特性。 主类的名字必须是:Main,否则按无效代码处理。
遇到这题,很多人的第一想法就是用暴破,的确,暴破是可以解出最后的答案的,但由于题目要求制约,最终时间会超时,所以啊,老老实实的用子列生成吧,由于篇幅太大,这里不做具体解释。
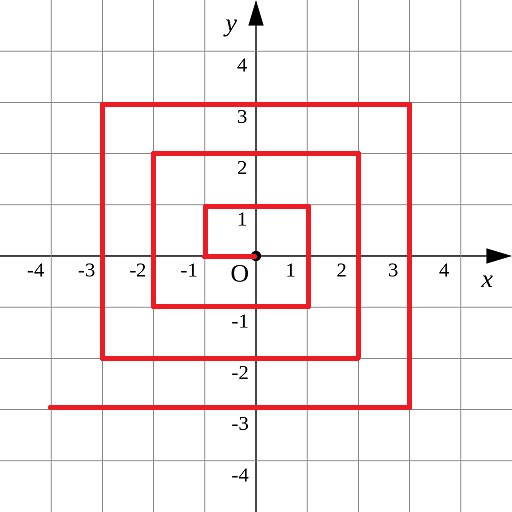
第七题:螺旋折线
如图所示的螺旋折线经过平面上所有整点恰好一次。 对于整点(X, Y),我们定义它到原点的距离dis(X,
Y)是从原点到(X, Y)的螺旋折线段的长度。例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y),你能计算出dis(X, Y)吗?
【输入格式】 X和Y
对于40%的数据,-1000 <= X, Y <= 1000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000【输出格式】 输出dis(X, Y)
【输入样例】 0 1
【输出样例】 3
资源约定: 峰值内存消耗(含虚拟机) < 256M CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。 不要使用> package语句。不要使用jdk1.7及以上版本的特性。
主类的名字必须是:Main,否则按无效代码处理。
 关于这一题,可以把每过一次折线当作一步,同时需要考虑四个象限中x,y的正负情况。
关于这一题,可以把每过一次折线当作一步,同时需要考虑四个象限中x,y的正负情况。
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int x = sc.nextInt(); int y = sc.nextInt(); boolean ok = false; int x1 = 0, y1 = 0,m=0,count=0; while(!ok){ if(x1==x&&y1==y){ ok = true; break; } m++; if(m%2==1){//奇数步 for(int i = 0; i
好了,技术有限,篇幅有限,就回忆到这里吧,继续滚回去学算法吧,毕竟太菜!!!!!

