python机器学习 二分类 混淆矩阵_机器学习实战_分类(二)
我们训练一个RandomForestClassifier,然后拿它的的ROC曲线和ROC AUC数值去跟SGDClassifier的比较。首先你需要得到训练集每个样例的数值。但是由于随机森林分类器的工作方式,RandomForestClassifier不提供decision_function()方法。相反,它提供了predict_proba()方法。Skikit-Learn分类器通常二者中的一个。predict_proba()方法返回一个数组,数组的每一行代表一个样例,每一列代表一个类。数组当中的值的意思是:给定一个样例属于给定类的概率。比如,70%的概率这幅图是数字 5。
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
method="predict_proba")
但是要画 ROC 曲线,你需要的是样例的分数,而不是概率。一个简单的解决方法是使用正例的概率当作样例的分数。
y_scores_forest = y_probas_forest[:, 1] # score = proba of positive class 预测为正例概率
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)
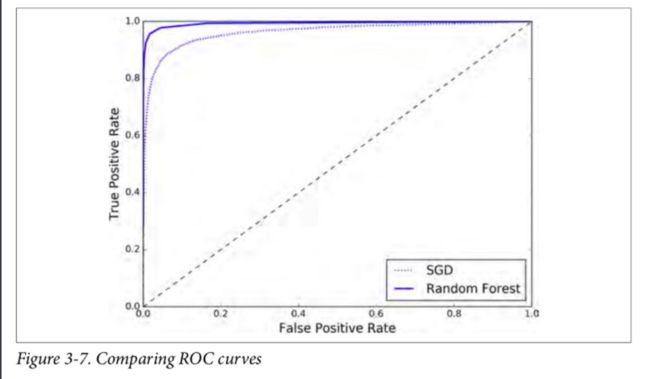
现在你即将得到 ROC 曲线。将前面一个分类器的 ROC 曲线一并画出来是很有用的,可以清楚地进行比较。
plt.plot(fpr, tpr, "b:", label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.legend(loc="bottom right")
plt.show()
如你所见,RandomForestClassifier的 ROC 曲线比SGDClassifier的好得多:它更靠近左上角。所以,它的 ROC AUC 也会更大。
>>> roc_auc_score(y_train_5, y_scores_forest)
0.99312433660038291
现在你知道如何训练一个二分类器,选择合适的标准,使用交叉验证去评估你的分类器,选择满足你需要的准确率/召回率折衷方案,和比较不同模型的 ROC 曲线和 ROC AUC 数值。现在让我们检测更多的数字,而不仅仅是一个数字 5。
多类别分类
一些算法(比如随机森林分类器或者朴素贝叶斯分类器)可以直接处理多类分类问题。其他一些算法(比如 SVM 分类器或者线性分类器)则是严格的二分类器。然后,有许多策略可以让你用二分类器去执行多类分类。
一个方法是:训练10个二分类器,每一个对应一个数字(探测器 0,探测器 1,探测器 2,以此类推)。然后当你想对某张图片进行分类的时候,让每一个分类器对这个图片进行分类,选出决策分数最高的那个分类器(One vs all 里面分数最高的One)。这叫做“一对所有”(OvA)策略
另一个策略是对每一对数字都训练一个二分类器:一个分类器用来处理数字 0 和数字 1,一个用来处理数字 0 和数字 2,一个用来处理数字 1 和 2,以此类推。这叫做“一对一”(OvO)策略。如果有 N 个类。你需要训练N*(N-1)/2个分类器。
一些算法(比如 SVM 分类器)在训练集的大小上很难扩展,所以对于这些算法,OvO 是比较好的,因为它可以在小的数据集上面可以更多地训练,较之于巨大的数据集而言。但是,对于大部分的二分类器来说,OvA 是更好的选择。Scikit-Learn 可以探测出你想使用一个二分类器去完成多分类的任务,它会自动地执行 OvA(除了 SVM 分类器,它使用 OvO)让我们试一下SGDClassifier.
>>> sgd_clf.fit(X_train, y_train) # y_train, not y_train_5
>>> sgd_clf.predict([some_digit])
array([ 5.])
上面的代码在训练集上训练了一个SGDClassifier。这个分类器处理原始的目标class,从 0 到 9(y_train),而不是仅仅探测是否为 5 (y_train_5)。然后它做出一个判断(在这个案例下只有一个正确的数字)。在幕后,Scikit-Learn 实际上训练了 10 个二分类器,每个分类器都产到一张图片的决策数值,选择数值最高的那个类。
为了证明这是真实的,你可以调用decision_function()方法。不是返回每个样例的一个数值,而是返回 10 个数值,一个数值对应于一个类。
>>> some_digit_scores = sgd_clf.decision_function([some_digit])
>>> some_digit_scores
array([[-311402.62954431, -363517.28355739, -446449.5306454 ,
-183226.61023518, -414337.15339485, 161855.74572176,
-452576.39616343, -471957.14962573, -518542.33997148,
-536774.63961222]])
最高数值是对应于类别 5 :
>>> np.argmax(some_digit_scores) # 找最大值的索引
5
>>> sgd_clf.classes_
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
>>> sgd_clf.classes[5] # 用索引匹配类别
5.0
一个分类器被训练好了之后,它会保存目标类别列表到它的属性classes_ 中去,按照值排序。在本例子当中,在classes_ 数组当中的每个类的索引方便地匹配了类本身,比如,索引为 5 的类恰好是类别 5 本身。但通常不会这么幸运。
如果你想强制 Scikit-Learn 使用 OvO 策略或者 OvA 策略,你可以使用OneVsOneClassifier类或者OneVsRestClassifier类。创建一个样例,传递一个二分类器给它的构造函数。举例子,下面的代码会创建一个多类分类器,使用 OvO 策略,基于SGDClassifier。
>>> from sklearn.multiclass import OneVsOneClassifier
>>> ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))
>>> ovo_clf.fit(X_train, y_train)
>>> ovo_clf.predict([some_digit])
array([ 5.])
>>> len(ovo_clf.estimators_)
45
训练一个RandomForestClassifier同样简单:
>>> forest_clf.fit(X_train, y_train)
>>> forest_clf.predict([some_digit])
array([ 5.])
这次 Scikit-Learn 没有必要去运行 OvO 或者 OvA,因为随机森林分类器能够直接将一个样例分到多个类别。你可以调用predict_proba(),得到样例对应的类别的概率值的列表:
>>> forest_clf.predict_proba([some_digit])
array([[ 0.1, 0. , 0. , 0.1, 0. , 0.8, 0. , 0. , 0. , 0. ]])
你可以看到这个分类器相当确信它的预测:在数组的索引 5 上的 0.8,意味着这个模型以 80% 的概率估算这张图片代表数字 5。它也认为这个图片可能是数字 0 或者数字 3,分别都是 10% 的几率。
现在当然你想评估这些分类器。像平常一样,你想使用交叉验证。让我们用cross_val_score()来评估SGDClassifier的精度。
>>> cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
array([ 0.84063187, 0.84899245, 0.86652998])
在所有测试折(test fold)上,它有 84% 的精度。如果你是用一个随机的分类器,你将会得到 10% 的正确率。所以这不是一个坏的分数,但是你可以做的更好。举例子,简单将输入正则化,将会提高精度到 90% 以上。
>>> from sklearn.preprocessing import StandardScaler
>>> scaler = StandardScaler()
>>> X_train_scaled = scaler.fit_transform(X_train.astype(np.float64)) # 特征正则化,没说用哪种
>>> cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
array([ 0.91011798, 0.90874544, 0.906636 ])
误差分析:
首先,你可以检查混淆矩阵。你需要使用cross_val_predict()做出预测,然后调用confusion_matrix()函数,像你早前做的那样。
>>> y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
>>> conf_mx = confusion_matrix(y_train, y_train_pred)
>>> conf_mx
array([[5725, 3, 24, 9, 10, 49, 50, 10, 39, 4],
[ 2, 6493, 43, 25, 7, 40, 5, 10, 109, 8],
[ 51, 41, 5321, 104, 89, 26, 87, 60, 166, 13],
[ 47, 46, 141, 5342, 1, 231, 40, 50, 141, 92],
[ 19, 29, 41, 10, 5366, 9, 56, 37, 86, 189],
[ 73, 45, 36, 193, 64, 4582, 111, 30, 193, 94],
[ 29, 34, 44, 2, 42, 85, 5627, 10, 45, 0],
[ 25, 24, 74, 32, 54, 12, 6, 5787, 15, 236],
[ 52, 161, 73, 156, 10, 163, 61, 25, 5027, 123],
[ 43, 35, 26, 92, 178, 28, 2, 223, 82, 5240]])
这里是一对数字。使用 Matplotlib 的matshow()函数,将混淆矩阵以图像的方式呈现,将会更加方便
plt.matshow(conf_mx, cmap=plt.cm.gray) # #灰度图,对应位置的值越大色块越亮
plt.show()
这个混淆矩阵看起来相当好,因为大多数的图片在主对角线上。在主对角线上意味着被分类正确。数字 5 对应的格子看起来比其他数字要暗淡许多。这可能是数据集当中数字 5 的图片比较少,又或者是分类器对于数字 5 的表现不如其他数字那么好。你可以验证两种情况.
让我们关注仅包含误差数据的图像呈现。首先你需要将混淆矩阵的每一个值除以相应类别的图片的总数目。这样子,你可以比较错误率,而不是绝对的错误数(这对大的类别不公平)。
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
现在让我们用 0 来填充对角线。这样子就只保留了被错误分类的数据。让我们画出这个结果。(此时数值为错误率)
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.show()
现在你可以清楚看出分类器制造出来的各类误差。记住:行代表实际类别,列代表预测的类别。第 8、9 列相当亮,这告诉你许多图片被误分成数字 8 或者数字 9。相似的,第 8、9 行也相当亮,告诉你数字 8、数字 9 经常被误以为是其他数字。相反,一些行相当黑,比如第一行:这意味着大部分的数字 1 被正确分类(一些被误分类为数字 8 )。留意到误差图不是严格对称的。举例子,比起将数字 8 误分类为数字 5 的数量,有更多的数字 5 被误分类为数字 8。
分析混淆矩阵通常可以给你提供深刻的见解去改善你的分类器。回顾这幅图,看样子你应该努力改善分类器在数字 8 和数字 9 上的表现,和纠正 3/5 的混淆。举例子,你可以尝试去收集更多的数据,或者你可以构造新的、有助于分类器的特征。举例子,写一个算法去数闭合的环(比如,数字 8 有两个环,数字 6 有一个, 5 没有)。又或者你可以预处理图片(比如,使用 Scikit-Learn,Pillow, OpenCV)去构造一个模式,比如闭合的环。
分析独特的误差,是获得关于你的分类器是如何工作及其为什么失败的洞见的一个好途径。但是这相对难和耗时。举例子,我们可以画出数字 3 和 5 的例子
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], ../images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], ../images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], ../images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], ../images_per_row=5)
plt.show()
左边两个5*5的块将数字识别为 3,右边的将数字识别为 5。一些被分类器错误分类的数字(比如左下角和右上角的块)是书写地相当差,甚至让人类分类都会觉得很困难(比如第 8 行第 1 列的数字 5,看起来非常像数字 3 )。但是,大部分被误分类的数字,在我们看来都是显而易见的错误。很难明白为什么分类器会分错。原因是我们使用的简单的SGDClassifier,这是一个线性模型。它所做的全部工作就是分配一个类权重给每一个像素,然后当它看到一张新的图片,它就将加权的像素强度相加,每个类得到一个新的值。所以,因为 3 和 5 只有一小部分的像素有差异,这个模型很容易混淆它们。
3 和 5 之间的主要差异是连接顶部的线和底部的线的细线的位置。如果你画一个 3,连接处稍微向左偏移,分类器很可能将它分类成 5。反之亦然。换一个说法,这个分类器对于图片的位移和旋转相当敏感。所以,减轻 3/5 混淆的一个方法是对图片进行预处理,确保它们都很好地中心化和不过度旋转。这同样很可能帮助减轻其他类型的错误。
多标签分类
先看一个简单点的例子,仅仅是为了阐明的目的
from sklearn.neighbors import KNeighborsClassifier
y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)
这段代码创造了一个y_multilabel数组,里面包含两个目标标签。第一个标签指出这个数字是否为大数字(7,8 或者 9),第二个标签指出这个数字是否是奇数。接下来几行代码会创建一个KNeighborsClassifier样例(它支持多标签分类,但不是所有分类器都可以),然后我们使用多目标数组来训练它。现在你可以生成一个预测,然后它输出两个标签:
>>> knn_clf.predict([some_digit])
array([[False, True]], dtype=bool)
它工作正确。数字 5 不是大数(False),同时是一个奇数(True)
有许多方法去评估一个多标签分类器,和选择正确的量度标准,这取决于你的项目。举个例子,一个方法是对每个个体标签去量度 F1 值(或者前面讨论过的其他任意的二分类器的量度标准),然后计算平均值。下面的代码计算全部标签的平均 F1 值:
>>> y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_train, cv=3)
>>> f1_score(y_train, y_train_knn_pred, average="macro")
0.96845540180280221
这里假设所有标签有着同等的重要性,但可能不是这样。特别是,如果你的 Alice 的照片比 Bob 或者 Charlie 更多的时候,也许你想让分类器在 Alice 的照片上具有更大的权重。一个简单的选项是:给每一个标签的权重等于它的支持度(比如,那个标签的样例的数目)。为了做到这点,简单地在上面代码中设置average="weighted"。
多输出分类
我们即将讨论的最后一种分类任务被叫做“多输出-多类分类”(或者简称为多输出分类)。它是多标签分类的简单泛化,在这里每一个标签可以是多类别的(比如说,它可以有多于两个可能值)。
为了说明这点,我们建立一个系统,它可以去除图片当中的噪音。它将一张混有噪音的图片作为输入,期待它输出一张干净的数字图片,用一个像素强度的数组表示,就像 MNIST 图片那样。注意到这个分类器的输出是多标签的(一个像素一个标签)和每个标签可以有多个值(像素强度取值范围从 0 到 255)。所以它是一个多输出分类系统的例子。
分类与回归之间的界限是模糊的,比如这个例子。按理说,预测一个像素的强度更类似于一个回归任务,而不是一个分类任务。而且,多输出系统不限于分类任务。你甚至可以让你一个系统给每一个样例都输出多个标签,包括类标签和值标签。
让我们从 MNIST 的图片创建训练集和测试集开始,然后给图片的像素强度添加噪声,这里是用 NumPy 的randint()函数。目标图像是原始图像。
noise = rnd.randint(0, 100, (len(X_train), 784))
noise = rnd.randint(0, 100, (len(X_test), 784))
X_train_mod = X_train + noise
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
让我们看一下测试集当中的一张图片(是的,我们在窥探测试集,所以你应该马上邹眉):
左边的加噪声的输入图片。右边是干净的目标图片。现在我们训练分类器,让它清洁这张图片:
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict([X_test_mod[some_index]])
plot_digit(clean_digit)
分类内容就这么多。