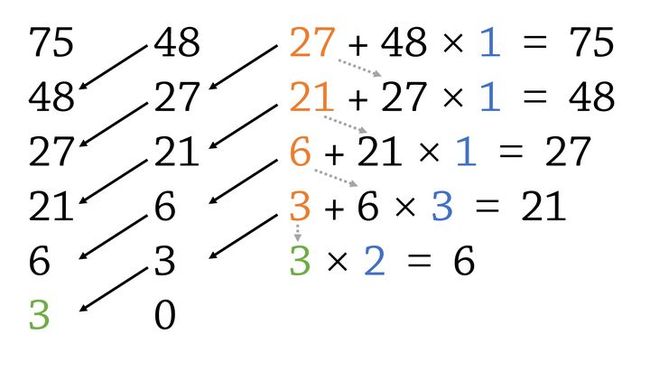周报(从1月7号起)
匆匆忙忙回到家,休息了几天,又要正式上班了,想想前几天还在对抗简单的最短路径问题,什么Floyd算法,什么dijkstra算法,确实难受,在高铁上我还试图ac题,很明显我太天真了,然后6号晚上的会议,通过学长和同学的分享在学校和家里的学习心得,我确实要更加努力了,学习计划也在当天晚上出炉了。
1月7号
上午上课的时候,重新复习了一下两种算法后,在学长的细心讲解下,(张暮冉学长确实讲的不错)又学习了两种新算法(还需要巩固),还是最短路径问题,Bellman_Ford算法和spfa算法,对于Bellman_Ford算法,时间复杂度为o(n*m),它的存图方式直接利用结构体就行了,然后主要思想是先循环n次,每一次循环所有边,就是遍历所有结构体数组,最后进行松弛操作,找到最短的,进行更新,主要处理的有负权边的最短路径问题,相比于spaf算法,虽然没有一点优势(这是实话),但是只能用Bellman_Ford算法去解决有限制边的最短路径问题,所以Bellman_Ford算法也要掌握好。
当然,重点还是spfa算法,而spfa算法还应用到了一个新的存图方式,链式前向星存图,链式前向星是用静态存储的邻接表,对于邻接表用结构体数组来模拟,分别储存u(起点),v(终点),w(权值),结构体里还有一个非常重要的next[i],表示表示与第i条边同起点的下一条边的存储位置,然后开一个head[i]数组,表示以 i 为起点的最后一条边的编号,令next=head,即将之前的前面一条边顺次的通过next联系起来,最后明白了链式前向星具有边集数组和邻接表的功能,属于静态链表,不需要频繁地创建结点,应用十分灵活。对于链式前向星的遍历,在遍历时是倒着遍历的,也就是说与输入顺序是相反的,不过这样不影响结果的正确性,这个链式前向星确实有点难理解,看了好多博客,最后在下面那个博客的介绍下完全理解了(3条消息) 深度理解链式前向星_ACdreamer-CSDN博客_链式前向星![]() https://blog.csdn.net/acdreamers/article/details/16902023
https://blog.csdn.net/acdreamers/article/details/16902023
然后就是对spfa算法的学习,存完图后,对数据的处理就需要运用队列,这是一个大问题,我对于队列的运用很少很少, 但是通过学习算法学习笔记(6):最短路问题 - 知乎 (zhihu.com)
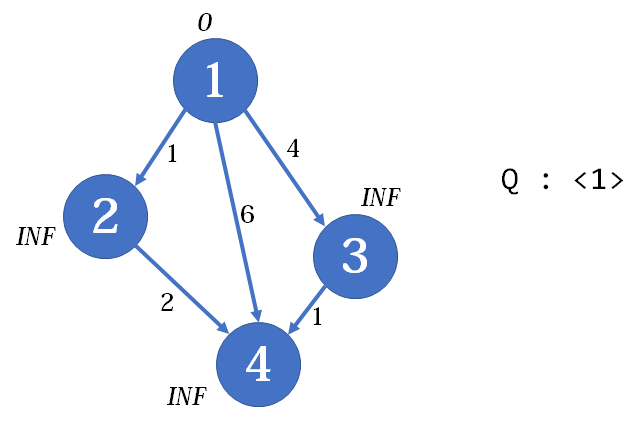
SPFA算法,也就是队列优化的Bellman-Ford算法,维护一个队列。一开始,把起点放进队列:
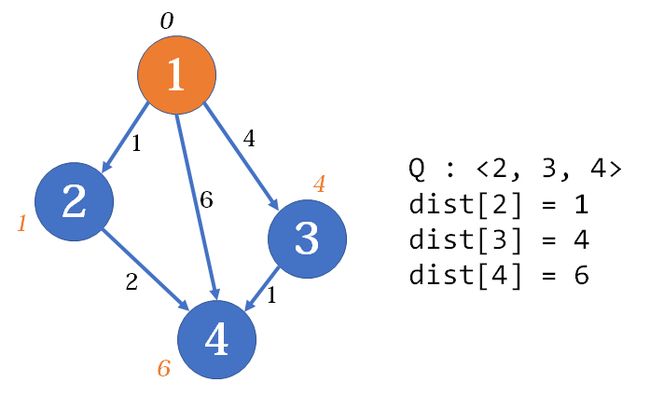
我们现在考察1号点,它可以到达点2、3、4。于是1号点出队,2、3、4号点依次入队,入队时松弛相应的边。
现在队首是2号点,2号点出队。2号点可以到达4号点,我们松弛2, 4,但是4号点已经在队列里了,所以4号点就不入队了(之后解释原因)。
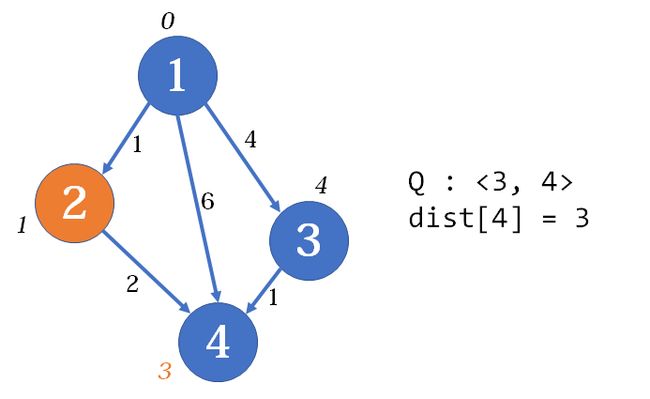
因为这张图非常简单,后面的流程我就不画了,无非是3号点出队,松弛3, 4,然后4号点出队而已。当队列为空时,流程结束。
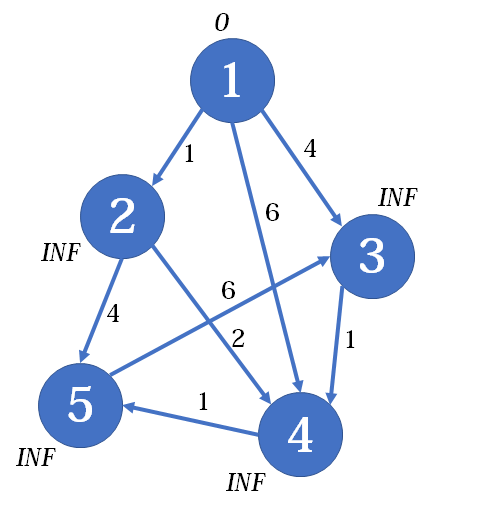
为了表明SPFA的优越性,我们再来看一个稍微复杂一点的图(在原图基础上增加一个5号点):
这张图,按照Bellman-Ford算法,需要松弛8*4=32次。现在我们改用SPFA解决这个问题。
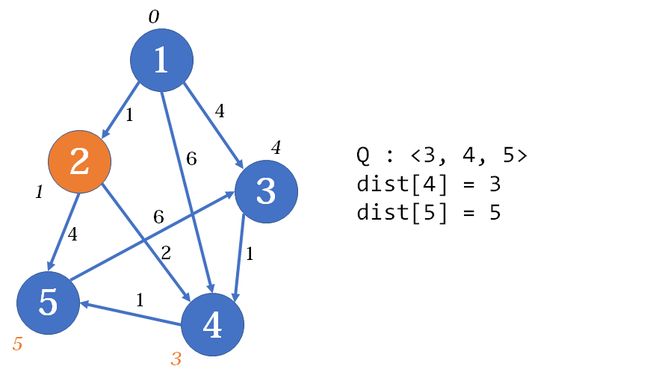
显然前几步跟上次是一致的,我们松弛了1, 2、1, 3、1, 4,现在队首元素是2。我们让2出队,并松弛2, 4、2, 5。5未在队列中,5入队。
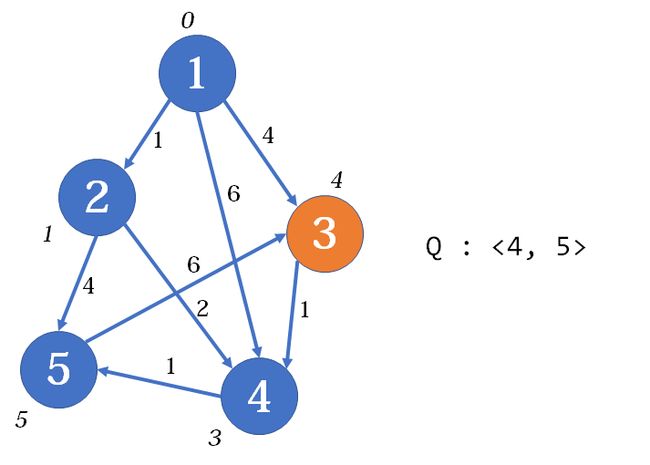
3号点没能更新什么东西:
然后4号点出队,松弛4, 5,然后5号点已在队列所以不入队。
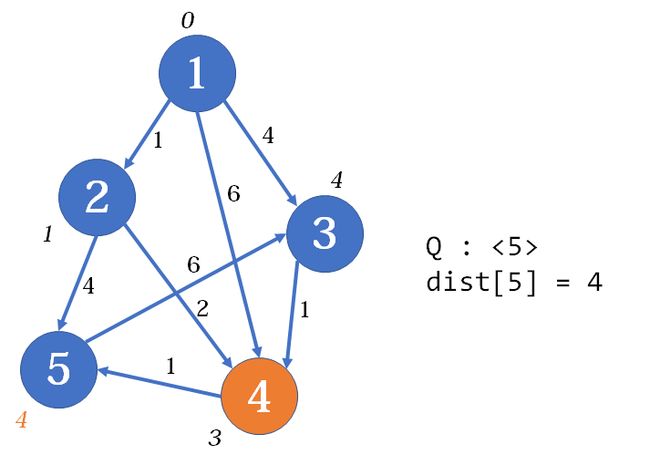
最后5号点出队,dist[3]未被更新,所以3号点通往的点不会跟着被更新,因此3号点不入队,循环结束。
最后总结一下队列的运用:
- 只让当前点能到达的点入队
- 如果一个点已经在队列里,便不重复入队
- 如果一条边未被更新,那么它的终点不入队
对于这一整天的学习,对最短路的几种简单算法有了不错的理解和感悟,并且通过学习知道什么时候用最短路的什么算法,对于这些算法的模板也要打清楚,多练习,vj上的题也要用新的方法去在做一遍,体会几种方法的不同和适用范围,不过堆优化版的dijkstra算法还是有点难理解,我感觉这个算法才是最短路里的伪通用算法(除了几种特殊的几种)所以之后重点去理解堆优化版dijkstra算法。
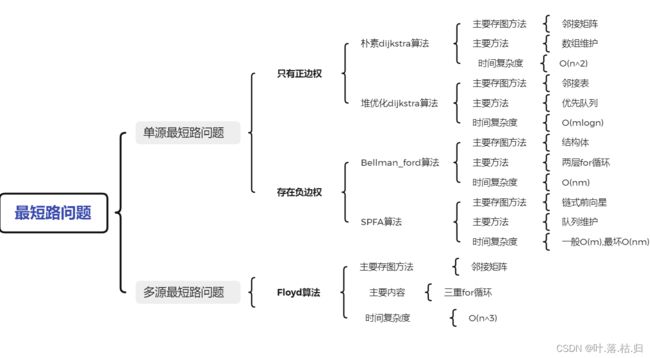
最后对最短路问题做了一个总结:
1月8号
刚理解学习玩最短路问题,上午8点就开始新的算法学习:最小生成树。听到树,就感觉很难,但听到郭学长的细心讲解后,对最小生成树有了一个大致的感觉,有的算法是培训前几天学习过的算法的结合,比如,对于最小生成树的Kruskal算法,这个算法运用了前面学习的并查集算法,至于prim算法来说,与dijkstra算法的模板类似,然后就要来探索一下他们的不同了吧!也就是说最小生成树与最短路径问题有哪些不同,下面是我在网上的找的对他们之间不同的很好的一个表格:
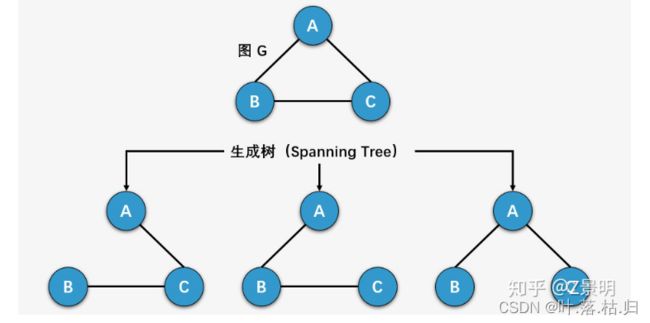
对于最小生成树,首先要明白生成树,我的理解是生成树就是一个环形无向图转换过来的无环无向图,下面这个由Z景明的图很好的表示了生成树,n个点,n-1条边。。。
而对于最小生成树来说,就是每一条边权值和最小的生成树。
最小生成树大致有两种算法;
1.Kruskal算法
2.Prim算法
因为学过相近思想,所以对最小生成树算法比较能理解和熟悉。
Kruskal算法
Kruskal算法利用并查集思想,使所有连通块连接在一块,当n-1条边都在一个集合里面,最小生成树就形成了,总的来说有以下三步:
1. 我们先用结构体把每条边的端点和权值记录下来,然后对每条边按权值进行排序
2. 因为使图连通最少需要n-1条边,所以我们依次从小到大遍历所有的边,如果该边的端点不在当前的连通分支中,则将其加入其中
3. 当遍历到最后一条边或添加边数超过n-1时,结束遍历
但还有一点要注意的,并不是每次算法得出的图都是连通的,如果边的数量没达到n-1就结束了遍历,即所有边都已经遍历完了,那我们所求的最小生成树就不存在。
Prim算法
Prim算法利用贪心思想,每一次都找到两点之间权值最小的点去更新下一个点,当每一个点都更新到了,最小生成树就形成了,总的来说有以下4步:
- 将连通网中的所有顶点分为两类(假设为 A 类和 B 类)。初始状态下,所有顶点位于 B 类;
- 选择任意一个顶点,将其从 B 类移动到 A 类;
- 从 B 类的所有顶点出发,找出一条连接着 A 类中的某个顶点且权值最小的边,将此边连接着的 A 类中的顶点移动到 B 类;
- 重复执行第 3 步,直至 B 类中的所有顶点全部移动到 A 类,恰好可以找到 N-1 条边。
学完两种最小生成树的实现算法,既复习了并查集算法和dijkstra算法,又对最小生成树和他们之间的用处进行了对比,尤其是Prim算法和dijkstra算法的基本类似的情况下,深度的理解了两个算法在不同问题中的用处。
然后接到一个突发情况!!!
单片机的学习任务要上检查了,我不得不晚上继续奋战,一口气看了好几个视频,在这里不得不说一句B站太nice了,真是学习的好地方,一个晚上单片机要学习的任务就完成了一半:独立按键的应用,用独立按键去实现LED灯的亮灭,反正整体来说今天的知识量有点大,以后还要好好消化巩固一下。
1月9号
昨天听学长说过,这一天的线段树很重要,所以早早的起来听我亲爱的超凡学长讲课了,然后超凡学长果然没让我失望,讲的真不错,每一处小细节都讲的很清楚,话不多说,直接来总结一下对于线段树的内容
首先线段树是算法竞赛中常用的用来维护区间信息的数据结构。是一名ACMer 需要掌握的一种基础、重要的数据结构线段树可以在O(logN)的时间复杂度内实现单点修改,区间修改,区间查询(区间求和,区间最大值、最小值,区间gcd )等操作
上午超凡学长给我们讲线段树的基础内容分为三个部分:
1.建树
2.单点修改
3.区间查询
建树
对于树的建立,主要是利用二分思想,对于树的每一个分支上的区间进行二分,从而形成线段树,线段树左枝和右枝由mid分开, 下面是以自己的理解做出的建树例子:
 每一个节点都有一段区间,上面就是一棵线段树,就是把所有的信息按顺序存在树中(其实就是开一个数组来分开存这些信息)。总的来说就是递归找节点,回溯更新节点。。。。
每一个节点都有一段区间,上面就是一棵线段树,就是把所有的信息按顺序存在树中(其实就是开一个数组来分开存这些信息)。总的来说就是递归找节点,回溯更新节点。。。。
区间查询
通过对区间的判断,来确定所需查询的范围,如果所需的区间对于所给区间,则直接返回区间的值,如果不是则进行递归回溯等一系列操作,以致最后找到所需所有区间的值
单点修改
这个部分是今天学习线段树的最难的部分,但是其实也是只有几个注意的地方,总的代码感觉就是对建树函数和区间查询函数的一些细节思想的综合。
虽然今天只讲了线段树的三个部分,但是还是比较难以理解,就算内容理解了一点,但是还要对代码的实现进行一些更深刻的理解,而且在对建树,区间查询,尤其是单点修改的时候还有一些细节要去深挖。
现在来罗列一些代码实现的细节
1.写一个结构体分别有四个数据:左区间 L ,右区间 R,记录每一个节点的值的sum,对于每一个区间的中间值mid。
2.写建树函数,第一步把左区间,右区间的值代入树中,然后判断左右区间是否相等,如果相等,则表示找到了节点,并进行对那个节点赋值,如果不相等则对刚开始的区间进行二分操作,即递归操作,直到把树建起来,就是所有的左区间等于右区间。当然有一个非常重要的函数记得加上去,就是每一次进行建节点的时候都要在回溯的时候对每一个节点的sum进行更新。。。(千万别忘记!!!)
3.写区间查询函数,首先判断输入区间是否为所找的区间,如果是返回当前区间的sum,如果不是,则进行递归查找,对输入区间进行二分判断,从而确定最后正确区间的sum,最后返回答案。
4.写单点修改函数,其实与区间查询差不多的操作,只是将区间判断改成了对节点的判断,然后进行二分查找,最后那个细节就是对pushup的更新,即对每一个子节点的父节点进行更新。
对于线段树建树,区间查询的模板理解了它操作过程,在完成对线段树模板题的套用后,也对线段树的模板有了更深刻的理解,逐步形成自己的风格。。
但是当我还对理解了线段树的一些基本操作后暗暗高兴的时候,51单片机的学习也不能落下,晚上6点之前完成对静态数码管的学习,然后去进行作业的完成.
作业分析:通过对独立按键进行操作使数码管上的一个地方显示数字,每按下一次独立按键,就对数码管进行操作,使数码管数字加一,然后到5后,再按下独立按键使数码管数字变成1,然后进行循环。
感受又是忙碌的一天,也是充满知识的一天!!!
1月10号
线段树的第一阶段学完,接下来就是第二阶段:
线段树的区间修改
这个时候很明显就要思考为什么会产生区间修改,其实也不难想到对一个线段长的数组去单点修改,时间复杂度会大到无法想象,所以这个时候就产生了区间修改,对于区间修改就要在结构体中加上一个标记lazy。
如果要求修改区间 L 到 R ,把所有包含在区间 L 到 R 中的节点都遍历一次、修改一次,时间复杂度无法承受。所以我们这里要引入一个叫做 「懒惰标记」 的东西。
懒惰标记,简单来说,就是通过延迟对节点信息的更改,从而减少可能不必要的操作次数。每次执行修改时,我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改,但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。
而要实现区间修改首先要进行pushdown操作,把父节点的lazy下放给子节点,在这些操作中,最难的点就是对pushdown的运用情况的判断,而对于pushdown操作来说,最重要的就是对lazy的清零操作。
然后区间修改的大致步骤
- 递归查找区间
- 发现现在区间完全属于需修改的区间,更新当前节点的信息,增加延迟标记。递归结束
- 若不完全属于则继续递归
但是在这个时候的区间查询也要进行一系列的变化,
即加上pushdown操作!!!
而对于建树上来说也要在赋值的时候把每一个lazy初始化为0
学完线段树的几种操作后,更多的是需要自己去熟悉和应用,用自己的方法去灵活应用。
尤其是区间修改的一系列操作,对于pushup和pushdown的操作位置的把握,线段树的学习就告一段落,我们的图论培训也要搞一个小结,所以晚上开了一次会议,学长们对我们的学习态度和一些问题做出了一总结,也让我们明白第一部的培训到一阶段,但是还有很多知识要自己去巩固和理解,不能忘记以前的知识也要打好精神学习新的知识。
咳咳,所以然后我就去运动放松自己了!!!
1月11号
培训阶段过了一个小结,上午原学长开始讲博弈论,对于博弈论,在新生培训阶段,就有学长讲了一个最基本的博弈论——巴什博弈。
而这一整天学习的博弈是系统的学习了一些博弈定理。
首先讲了一些关于博弈论的一些依托事件:
1.公平组合游戏
2.非公平组合游戏
3.反常游戏
然后依托这些事件重新讲了对应的博弈定理:
1.巴什博弈(同余定理)
二人游戏,一堆石子一共n个,两人轮流进行,每步可以取走1~m个石子,最先取光者获胜。
核心:判断n是否能整除m+1,如果能整除,那么先手必败,否则先手必胜
n%(m+1)=0 必败态:不管如何操作,下一个局面都是必胜态
n%(m+1)=x(x属于1到m) 必胜态:一定有一个操作使下一个局面变成必败态
if(n%(m+1)==0) cout<<"后手必胜"<一轮最多拿的就是1+m个,所以控制下去,最后的不到(1+m)的物品肯定会被后手拿到的。
2.尼姆博弈(异或定理)
有任意堆物品,每堆物品的个数是任意的,双方轮流从中取物品,每一次只能从一堆物品中取部分或全部物品,最少取一件,取到最后一件物品的人获胜。
核心:把每堆物品数全部异或起来,如果得到的值为0,那么先手必败,否则先手必胜。
a1^a2^a3^...an=0 必败态:不管如何操作,下一个局面都是必胜态
a1^a2^a3^...^an=x(x!=0) 必胜态:一定有一个操作使下一个局面变成必败态
for(int i=0;i>ans;
res^=ans;
}
if(res==0) cout<<"后手必胜"< 使必胜态变成必败态,只需要在n个数中找一个a[k],使得a[k]>a[k]^x,所以就能用a[k]^x去替换a[k],最后整个式子变为0;而使必败态变成必胜态,随便异或一个数,最后都不为0,
3.威佐夫博弈(黄金分割)
有两堆各若干的物品,两人轮流从其中一堆取至少一件物品,至多不限,或从两堆中同时取相同件物品,规定最后取完者胜利。
题目细节:
1.任意一堆中取出至少一个
2.同时从两堆中取得同样多的物品
核心:(n1,n2为两堆物品)判断两个数的差值t是不是满足 (sqrt(5)+1)/2*t==min(n1,n2)
if(n1>n2)
swap(n1,n2); //对n1,n2的大小进行判断
res=floor((n2-n1)*(1+sqrt(5.0))/2.0);
if(res==n1) cout<<"后手必胜"<4.斐波那契博弈
有一堆物品,两人轮流取物品,先手最少取一个,至多无上限,但不能把物品取完,之后每次取的物品数不能超过上一次取的物品数的二倍且至少为一件,取走最后一件物品的人获胜。
核心:先手胜当且仅当n不是斐波那契数(n为物品总数)
首先理解一下齐肯多夫定理,
齐肯多夫定理:任何正整数都可以唯一地表示成若干个不连续的斐波那契数之和。
以F(n)来表示第n个斐波那契数。m为任意正整数。
当m=1,2,3时,因为1=F(2),2=F(3),3=F(4),所以命题成立。下面采用数学归纳法证明定理对任何m均成立。
假设定理对任何小于m的正整数数都成立。下证命题对m也成立。
(1)若m是斐波那契数,则命题对m也成立。
(2)若m不是斐波那契数,设n1是满足F(n1)< m < F(n1 +1)的最大正整数。
设m'=m-F(n1),则m'=m-F(n1)
因此,命题对m也成立。
综合(1)(2),由数学归纳法,齐肯多夫定理对任何正整数m都成立。
虽然我也不了解为什么要去对一个数是否为斐波那契数进行判断,但是记住模板就行了,嘿嘿嘿,感觉没毛病,总之,四种的博弈游戏的规律模板,已经能够运用了,一整天对博弈论的学习还是很有效率的,不仅把原来的博弈论学习进行了巩固,还对其他几个基本情况进行了学习,题目简单,就是对模板的运用,不过要是深入理解还是比较困难的,所以以后有时间还要系统的去学习一下思想,(毕竟学长有的都不懂),任重而道远啊!!!对了,学长辛苦了,讲了两个小时,真辛苦。。。
1月12号
对于这一整天的学习:欧几里德算法的复习和扩展欧几里得算法的学习
欧几里得就是用来求最大公约数,主要思路就是利用辗转相除法使两个人找到最大公约数。
代码如下:
int gcd(int a, int b)
{
if (b == 0)
return a;
else
return gcd(b, a%b);
}欧几里得算法部分我们好像只能用来求解最大公约数,但是扩展欧几里德算法就不同了,我们既可以求出最大公约数,还可以顺带求解出使得:
a*x + b*y = gcd 的通解 x 和 y
扩展欧几里德算法的应用主要有以下三方面:
(1)求解不定方程;
(2)求解模线性方程(线性同余方程);
(3)求解模的逆元;
其中扩展欧几里得算法一个重要的应用在求解形如 a*x +b*y = c 的特解,比如一个数对于另一个数的乘法逆元
那么,什么是拓展欧几里得呢?这是一种算法,它可以在辗转相除途中求出不定方程 的一组解。
注意到上图中倒数第二行的 ,可以改写为 ,也就是说 可以被表示为 和 的线性组合。
然后倒数第三行, ,说明 可以被表示为 和 的线性组合,那么 也就可以被表示为 和 的线性组合。具体地,我们有:
这样一路推下去,即知 可以表示为 和 的线性组合。那么 就能找到解了。
然后给出模板:
int exgcd(int a, int b, int &x, int &y)
{
if (b == 0)
{
x = 1;
y = 0;
return a;
}
int d = exgcd(b, a % b, x, y), x0 = x, y0 = y;
x = y0;
y = x0 - (a / b) * y0;
return d;
}我自己对于这个扩展欧几里得算法的感觉就是对欧几里得算法的灵活运用,哈哈,难怪是扩展,就是对它的应用加多了嘛!!!可惜了,还是有点不理解里面的一些细节部分,还是得抽个时间去深究它!!!当然还是要说一句原学长真辛苦,两天接近4个小时了,我们真不能辜负他的心了。。。
1月13号
一大早就起床了,谁知道学长九点上课,刚好复习了一下扩展欧几里得算法,然后找了个博客看了一下,发现都是大佬,真强,强烈推荐扩展欧几里得与乘法逆元 - 王陸 - 博客园 (cnblogs.com)
对于这个问题我们观察到:欧几里德算法停止的状态是: a= gcd , b = 0 ,那么,这是否能给我们求解 x y 提供一种思路呢?因为,这时候,只要 a = gcd 的系数是 1 ,那么只要 b 的系数是 0 或者其他值(无所谓是多少,反正任何数乘以 0 都等于 0 但是a 的系数一定要是 1),这时,我们就会有: a*1 + b*0 = gcd
当然这是最终状态,但是我们是否可以从最终状态反推到最初的状态呢?
假设当前我们要处理的是求出 a 和 b的最大公约数,并求出 x 和 y 使得 a*x + b*y= gcd ,而我们已经求出了下一个状态:b 和 a%b 的最大公约数,并且求出了一组x1 和y1 使得: b*x1 + (a%b)*y1 = gcd , 那么这两个相邻的状态之间是否存在一种关系呢?
我们知道: a%b = a - (a/b)*b(这里的 “/” 指的是整除,例如 5/2=2 , 1/3=0),那么,我们可以进一步得到:
gcd = b*x1 + (a-(a/b)*b)*y1
= b*x1 + a*y1 – (a/b)*b*y1
= a*y1 + b*(x1 – a/b*y1)
对比之前我们的状态:求一组 x 和 y 使得:a*x + b*y = gcd ,是否发现了什么?
这里:
x = y1
y = x1 – a/b*y1
解决一个问题真开心啊,然后刚刚好,学长开始上课,课上的安排分了几个部分,所以毫不意外讲了很久,真是辛苦这些学长了,分为
| 1.复习同余 | 2.学习逆元 |
| 3.线性筛的学习 | 4.欧拉定理的学习 |
| 5.欧拉定理的证明(课下) | 6.STL的学习 |
同余在这里就不说了,直接进入逆元,
对于逆元这个问题,我的理解就是为了解决模意义下的除法问题。很直接吧,没毛病吧
而对于逆元有很多解决办法,昨天学习的扩展欧几里得算法就可以解决逆元问题,
整体上可以分为下面几种方法:
| 1.拓展欧几里得 |
|---|
| 2.费马小定理 |
| 3.线性递推 |
学长讲了1和2求逆元的代码,
1.
ll exgcd(ll a, ll b, ll &x, ll &y)// 拓展欧几里得
{
if (b == 0)
{
x = 1;
y = 0;
return a;
}
ll d = exgcd(b, a % b, y, x);
y -= (a / b) * x;
return d;
}
ll inv(ll a, ll p)//求逆元
{
ll x, y;
if (exgcd(a, p, x, y) != 1) // 无解的情形
return -1;
return (x % p + p) % p;
}2.费马小定理
inline ll qpow(ll a, ll n, ll p)// 快速幂
{
ll ans = 1;
while (n)
{
if (n & 1)
ans = ans % p * a % p;
a = a % p * a % p;
n >>= 1;
}
return ans;
}
inline ll inv(ll a, ll p)
{
return qpow(a, p - 2, p);
}想去了解更多推荐算法学习笔记(9):逆元 - 知乎 (zhihu.com)
至于对于剩下的几个内容,就没怎么听下去了,没办法鼻炎又发作了,只能等以后去补了,然后本周的报告到此就结束了,虽然有一些突发情况,但是整体上学习的内容和经验都让我收获满满,希望学长不会说我,发现我会补回来的,咳咳,尤其是STL,太多东西需要去学习和应用了。继续努力吧!!!大家一起加油!!!