(泰迪云课堂)-第5模块: 使用scikit-learn构建模型

目录

一、使用sklearn转换器处理数据

二、将数据集划分为训练集和测试集

三、利用转化器进行数据转化操作

四、构建并评价聚类模型

 五、构建并评价分类模型

六、构建并评价回归模型

---

一、使用sklearn转换器处理数据

#使用scikit-learn构建模型

#使用sklearn转换器处理数据

from sklearn.datasets import load_breast_cancer #导入的这个是类
cancer = load_breast_cancer()  #因为导入的是类，所以应该实例化
                               #实例化的时候注意右面的括号(),不要落下
                               #类 类似于一个字典

#print(cancer)
print(cancer.keys())
#print(cancer['data'])
#print(cancer['data'].shape)
#print(['target'])

#print(cancer['DESCR'])   #描述
#print(cancer['filename'])   #找到数据所处的位置

from sklearn.datasets import load_iris
iris = load_iris()

print(iris.keys())

二、将数据集划分为训练集和测试集

#将数据集划分为训练集和测试集
X_train,X_test,y_train,y_test = train_test_split(iris['data'],
                                                 iris['target'],
                                                 test_size=0.2,
                                                 stratify = iris['target'])
#stratify = iris['target']  这个参数是保证按照标签进行分层抽样

a = pd.Series(y_train).value_counts()#使用pandas进行频次的统计
print(a)  #频次是不均匀的，是不平衡数据，这样是会影响性能的

三、利用转化器进行数据转化操作

#sklearn 里面有函数可以进行数据转化操作，如下表所示：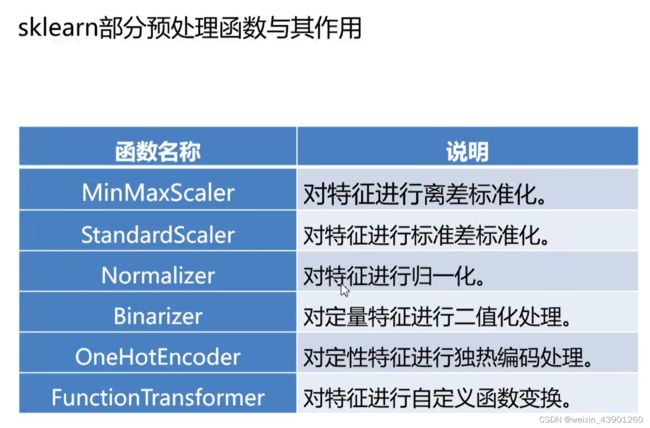

#sklearn 里面有函数可以进行数据转化操作
from sklearn.preprocessing import MinMaxScaler  #离差标准化,导入的这个是类

min_max_scaler = MinMaxScaler().fit(X_train) #要依靠一定的规则生成转化器
   #这个转换器是按照X_train里面的数据的最大值和最小值进行转化的
a = min_max_scaler.transform(X_train) #执行数据的转化操作
b = min_max_scaler.transform(X_test)  #注意：这个转化器是按照X_train的数据生成的

#可以用以下这个方法进行一步数据转化操作，但是不会有转化器的存在
c = MinMaxScaler().fit_transform(X_train)
print(c)

四、构建并评价聚类模型

 评价的算法：

#四、构建并评价聚类模型
from sklearn.cluster import KMeans  #导入KMeans类
from sklearn.metrics import adjusted_rand_score  #导入一个兰德系数评价指标，有标签的
from sklearn.metrics import silhouette_score  #这个系数不需要标签 轮廓系数

k_means = KMeans(n_clusters=3) #3个类中心
k_means.fit(iris['data'])   #执行聚类操作

#print(k_means.labels_)  #注意后面的这个“_”，不要落下,看聚类结果
#print(k_means.cluster_centers_)#查看聚类中心数

#help(adjusted_rand_score)  #查看参数要求和计算的公式

#利用兰德系数对聚类模型进行效果评析(有标签的)
e = adjusted_rand_score(iris['target'],k_means.labels_)#前面是真实值，后面是预测值
#print(e)

'''
#这个系数不需要标签 轮廓系数
#这个系数，取不同的类中心数(n_clusters=?)，找畸变最大的，
#就是说拐点处斜率最大的，可以通过画图看到
'''
f = silhouette_score(iris['data'],k_means.labels_) 
#print(f)

'''用以下函数循环并且画图'''

import matplotlib.pyplot as plt

scores = []
for k in range(2,7):
    '''构建并训练模型'''
    kmeans= KMeans(n_clusters = k,random_state=123).fit(iris['data'])
    score = silhouette_score(iris['data'],kmeans.labels_) 
      #这里的kmeans.labels_跟前面少了一个“_”是因为前面的重新定义了以下
    scores.append(score)
    print('iris数据聚%d类calinski_harabaz指数为：%f'%(k,score))
    #%s,%r,%d分别表示字符串以str（），rper(),以及十进制整数表示，%f表示结果为浮点型
plt.figure(figsize=(10,6))
plt.xticks(fontsize=20)  #x轴的字体变大
plt.yticks(fontsize=20)  #y轴的字体变大
plt.plot(range(2,7),scores,linewidth=1.5,linestyle="-")
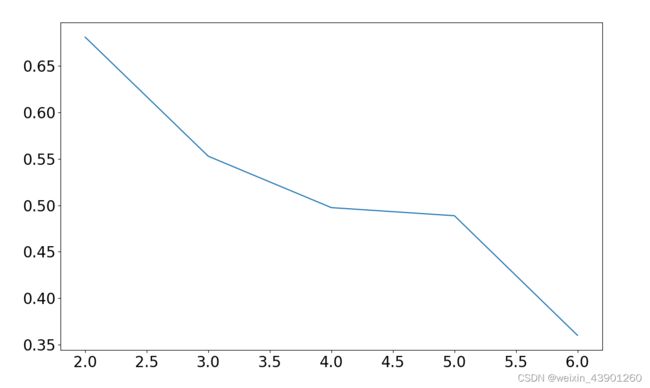
plt.show()

运算结果如下：

iris数据聚2类calinski_harabaz指数为：0.681046
iris数据聚3类calinski_harabaz指数为：0.552819
iris数据聚4类calinski_harabaz指数为：0.497455
iris数据聚5类calinski_harabaz指数为：0.488749
iris数据聚6类calinski_harabaz指数为：0.359943

画出的图如下所示：

 如图所示为聚类中心数为 5 时，畸变程度最大，所以选择聚类数为5

轮廓系数评价法，这个不需要原始的标签。

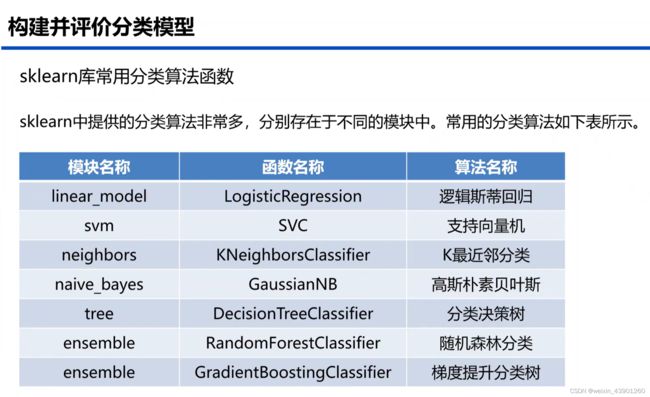
 五、构建并评价分类模型

#构建并评价分类模型
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report

iris = load_iris(return_X_y=True)#只需要得到iris里的X和y，所以要用这个参数
#print(iris)

X = iris[0]  #默认X是大写
y = iris[1]  #默认y是小写

X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,stratify=y)

clf = DecisionTreeClassifier()  #实例化决策树分类器，必须实例化，实例以后，这个模型就可以用了
clf.fit(X_train,y_train)        #训练模型

#print(clf.classes_)  #训练的结果类型
#print(clf.feature_importances_)  #鸢尾花一共有四个特征，打印四个特征的重要性程度

predicted = clf.predict(X_test)
#print(predicted)
#print(y_test)

precise = (predicted == y_test).mean()  #精确度
#print(precise)

report = classification_report(y_test,predicted)  #实例化一下，分类报告就整齐了
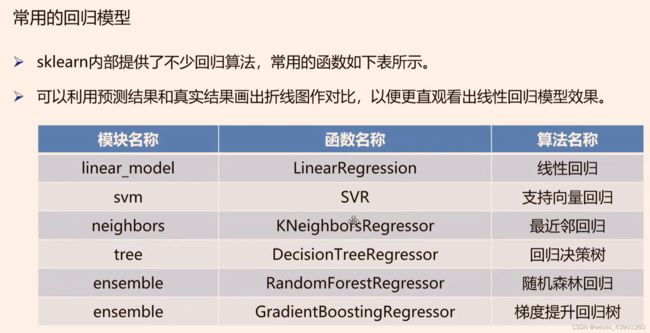
#print(report)

六、构建并评价回归模型

 

回归模型的评价指标：

#构建并评价回归模型

from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split 
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error #导入均方误差

boston = load_boston()   #实例化
#print(boston.keys())  #查看关键词
#print(boston['data'].shape)
#print(boston['target'].shape)

X_train, X_test,y_train,y_test = \
    train_test_split(boston['data'],boston['target'],test_size=0.2)
    
model = LinearRegression().fit(X_train,y_train) #模型训练并保存
                 #实例化以后就可以把模型保存
#print(model.coef_)   #打印模型的系数
#print(model.intercept_)   #打印模型的截距项系数

#评价回归模型
predicted = model.predict(X_test)
#print(predicted) #打印预测结果

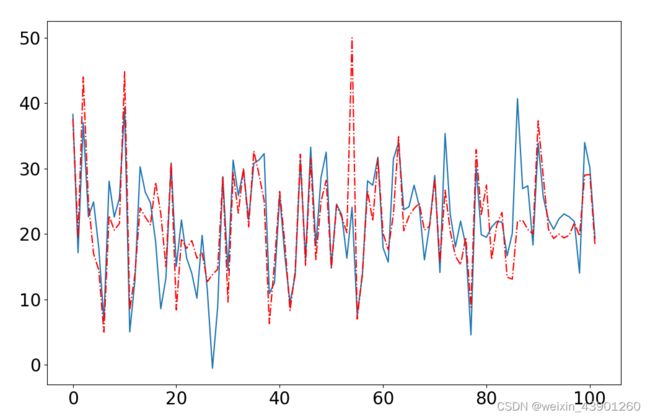
#画图看差距
plt.figure()
plt.plot(range(len(y_test)),predicted)
plt.plot(range(len(y_test)),y_test,'r-.')
plt.show()

#指标量化体现模型的性能---均方误差
error = mean_squared_error(y_test, predicted) 
print(error)

图示体现结果：

 均方误差量化结果：27.678330065546614