机器学习-有监督学习-集成学习方法(一):集成(Ensemble)学习方法综述【Bootstrap(Bagging装袋、Boosting提升)、Stacking堆叠、Blending融合】
一、集成学习方法(Ensemble Learning)
集成学习方法:通过建立几个分类(学习)器/模型组合的来解决单一预测问题。它的工作原理是生成多个分类(学习)器/模型,各自独立地学习和作出预测。这些预测最后结合成单预测,因此优于任何一个单分类的做出预测。
集成学习方法:都建立在一个这样的假设上:将多个模型组合在一起通常可以产生更强大的模型。
集成学习方法:是通过训练弱干个弱学习器,并通过一定的结合策略,从而形成一个强学习器。有时也被称为多分类器系统(multi-classifier system)、基于委员会的学习(committee-based learning)等。
集成学习方法先产生一组“个体学习器”(individual learner),再用某种策略将它们结合起来。通常来说,很多现有的学习算法都足以从训练数据中产生一个个体学习器。一般来说,我们会将这种由个体学习器集成的集成后的算法分为两类:
- 同质(homogeneous)集成,即集成中仅包含同种类型的一个体学习器,像“决策树集成”中就仅包含决策树,“神经网络集成”中就全是神经网络。同质集成中的个体学习器又称为基学习器(base learner),相应的学习算法也被称为基学习算法(base learning algorithm)。比如:Bagging、Boosting集成学习方法。
- 异质(heterogenous)集成,相对同质,异质集成中的个体学习器就是由不同的学习算法生成的,这时,个体学习器就被称为组件学习器(component learner)。比如:Stacking集成学习方法。
1、分类器的强弱
1.1 弱分类器
如果一个分类器的分类准确率在60%-80%,即:比随机预测略好,但准确率却不太高,我们可以称之为“弱分类器”,比如决策树(CART)。
- 多个弱分类器组合使用可以形成一个强分类器。比如基于决策树的随机森林。
1.2 强分类器
如果一个分类器的分类准确率在90%以上,则是“强分类器”,比如逻辑(Logistic)回归、支持向量机(SVM)。
- 使用单个逻辑回归分类器时,只要给的数据及特征足够好,一定可以把样本分类的足够好。
- 多个强分类器的集成后的分类器的效果也与单个强分类器的效果也差不多。不建议使用强分类器作为基分类器,因为它如果造成某特征或某样本的过拟合,不容易被平滑掉。
实践中,弱分类器在集成学习中的作用仅仅是提供了一个训练方向(就是看弱训练在那个特征(或者叫方向)上面的误差最大),然后在这个方向上面增强训练权值,即所谓强训练。最后组合起来的就是最终的结果。可以看到弱训练只是要提供一个好的训练方向就行了,而强训练才是最终模型优良的关键,强分类器的设计在于如何组合。
2、集成学习方法的目的
多分类器进行组合的目的:是为了将单个分类器(也叫基分类器 base classifier)进行组合,提升对未知样本的分类准确率,(依赖于基分类器的分类性能和基分类器之间的独立性)。构建组合分类器的逻辑视图可以用以下的图表示:

3、集成学习方法的误差
就机器学习算法来说,其泛化误差可以分解为两部分,偏差(bias) 和 方差(variance)。
![]()
- 偏差:指的是算法的期望预测与真实预测之间的偏差程度,反应了模型本身的拟合能力;
- 方差:度量了同等大小的训练集的变动导致学习性能的变化,刻画了数据扰动所导致的影响。
![]()
如上图所示:
-
当模型越简单时,即使我们再换一组数据,最后得出的学习器和之前的学习器的差别就不那么大,模型的方差很小。还是因为模型简单,所以偏差会很大。
-
当模型越复杂时,拟合的程度就越高,模型的训练偏差就越小。但此时如果换一组数据可能模型的变化就会很大,即模型的方差很大。所以模型过于复杂的时候会导致过拟合。
-
当我们训练一个模型时,偏差和方差都得照顾到,漏掉一个都不行。
-
对于Bagging算法:能够减小训练方差(Variance)。由于我们会并行地训练很多不同的分类器,因为采用了很多个相互独立的基分类器,总体上实现了整体模型的方差(Variance) 最小化。所以对于每个基分类器来说,首要任务就是如何降低偏差(Bias),所以我们会采用深度很深甚至不剪枝的决策树。
-
对于Boosting:能够减小训练偏差(Bias)。每一步我们都会在上一轮的基础上更加拟合原数据,总体上实现了整体模型的偏差(Bias)最小化。所以对于每个基分类器来说,首要任务就是如何降低方差(Variance),即选择更简单的分类器,所以我们采用深度很浅的决策树。
二、集成学习方法分类
集成学习的三大典型方法:
- Bagging 并行集成
- Boosting 串行集成
- Stacking 分层集成
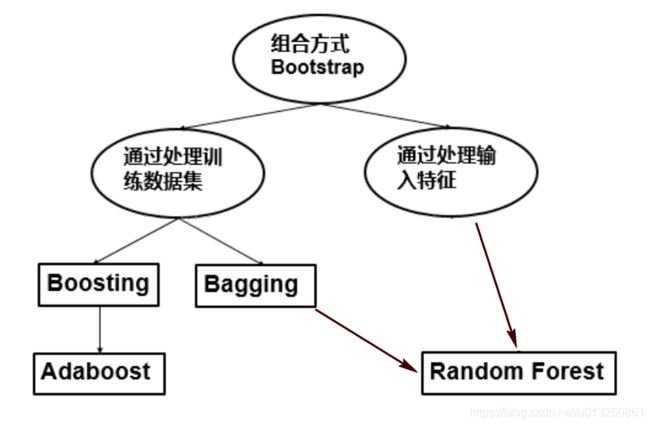
提到组合方法(classifier combination),有很多的名字涌现,如:Bootstrap、Bagging、Random Forest、Boosting、Adaboost、GBDT、XGBoost、Stacking、 Blending等等。它们之间的关系可用下图来表示:

决策树、随机森林、GBDT、XGBoost之所以能做回归(并不是线性回归),是因为能够用决策树的方式来拟合曲线。
- Boostrap是靴子的带子的意思,名字来源于“pull up your ownboostraps”,意思是通过拉靴子提高自己,本来的意思是不可能发生的事情,但后来发展成通过自己的努力让事情变得更好。放在组合分类器这里,意思就是通过分类器自己提高分类的性能。
- Boostrap只是提供了一种组合方法的思想,就是将基分类器的训练结果进行综合分析,而其它的名称如Bagging。Boosting是对组合方法的具体演绎。
- Boostrap组合方法分为:Bagging算法与Boosting算法。
- Bagging的作用:降低“方差”;
- Boost的作用:降低“偏差”;
- 通过处理训练数据集:这种方法根据某种抽样分布,通过对原始数据集进行再抽样来得到多个数据集。抽样分布决定了一个样本被选作训练的可能性大小,然后使用特定的学习算法为每个训练集建立一个分类器。Bagging(袋装)和Boosting(提升)都是这样的思想。Adaboost是Boosting当中比较出众的一个算法,是一种自适应(Adapt)提升。
- 通过处理输入特征:在这种方法中,通过选择输入特征的子集来形成每个训练集。Random Forest(随机森林)就是通过处理输入特征的组合方法,并且它的基分类器限制成了决策树。
三、Bootstrap
Bootstrap具体的方法是:
- 采用有放回重复抽样的方法每次从 n n n 个原始样本中抽取 m m m 个样本( m m m 自己设定);
- 对于 m m m 个样本计算统计量;
- 重复步骤(1)、(2) N N N 次( N N N 一般大于1000),这样就可以算出 N N N 个统计量;
- 计算这 N N N 个统计量的方差
比如说,我现在要对一些未知样本做分类,分类算法选取一种,比如SVM 。我要估计的总体参数是准确率(accuracy)。对于 n n n 个原始样本,从步骤(1)开始,每次对抽取出的样本用SVM训练出一个模型,然后用这个模型对未知样本做分类,得到一个准确率。重复 N N N 次,可以得到 N N N 个准确率,然后对计算出的 N N N 个准确率做方差。
我在考虑为什么要计算这 N N N 个统计量的方差而不是期望或者均值。方差表示的是一组数据与其平均水平的偏离程度,如果计算的方差值在一定范围之内,则表示这些数据的波动不是很大,那么他们的均值就可以用来估计总体的参数,而如果方差很大,这些样本统计量波动很大,那么总体的参数估计就不太准确。
1、Random Forest、Adaboost、GBDT、XGBoost的主要区别
| Random Forest (Bagging) |
Adaboost (Boosting) |
GBDT (Boosting) |
XGBoost (Boosting) |
|
|---|---|---|---|---|
| 基分类器 | 分类决策树、回归决策树 | 分类决策树、回归决策树 | 回归决策树, 但也可以解决分类问题(设置阈值) |
回归决策树、线性分类器(LR)、线性回归 |
| 节点分裂方式 | ID3用信息增益, C4.5用信息增益率, CART分类用基尼指数, CART回归用选择最优切分特征和值对(j,s) |
选择最优切分特征和值对(j,s) | 优化推导,详见附注 | |
| 基分类器 权重 |
所有的弱分类器权值相同 | 误差越小的弱分类器其权值越大 | 误差越小的弱分类器其权值越大 | 误差越小的弱分类器其权值越大 |
| 样本选择 | 随机有放回的取样 | 每一轮训练的样本是固定的 | 每一轮训练的样本是固定的 | 每一轮训练的样本是固定的 |
| 样本权重 | 均匀取样,且每个样本的权重相同 | 根据错误率调整样本权重, 错误率越大的样本权重会变大 |
每个样本的权重始终不变 | |
| 并行计算 | 个体学习器之间不存在强依赖关系, 各个预测函数可以并行生成 |
树串行生成 个体学习器之间存在较强的依赖性, 各个预测函数必须按照顺序迭代生成 |
树串行生成 | 树串行生成,特征粒度上的并行, 各个特征的增益计算可以开多线程进行 |
| 损失函数 | 平均方差 | 指数损失函数 L ( y , f ( x ) ) = 1 n ∑ i = 1 n e − y i f ( x i ) L(\textbf{y},f(\textbf{x}))=\frac1n\sum^n_{i=1}e^{-y_if(x_i)} L(y,f(x))=n1i=1∑ne−yif(xi) |
默认为平均方差 ( 残差树版本) 或自定义Loss(例如LambdaMart), 只用到一阶导数信息(梯度) |
XGBoost则对代价函数进行了二阶泰勒展开, 同时用到了一阶和二阶导数。 代价函数加入正则项(树的叶子节点个数、 每个叶子节点上输出的score的L2模的平方和), 且同时用到了一阶g和二阶导数h |
2、将决策树与各种集成学习方法组合成新的算法
- Bagging + 决策树 = 随机森林
- AdaBoost + 决策树 = 提升树
- Gradient + 决策树 = GDBT
3、Bagging(Boostrap Aggregation)
Bagging是Boostrap Aggregation的缩写,是一种根据均匀概率分布从数据集中重复抽样(有放回的)的技术。子训练样本集的大小和原始数据集相同。在构造每一个子分类器的训练样本时,由于是对原始数据集的有放回抽样,因此同一个训练样本集中可能出现多次同一个样本数据。
- 从训练样本集中(有放回的)重复抽样选出 n n n 个样本;在所有特征属性上,对这 n n n 个样本建立基分类器(ID3、C4.5、CART、SVM、Logistic回归等);
- 重复步骤(1) m m m 次,获得 m m m 个基分类器;
- 利用这 m m m 个基分类器分别对测试样本集进行分类判断,测试样本集中的各个样本属于哪一类,是由这 m m m 个基分类器各自的判断结果中的众数最终决定,即由所有单个基分类器的预测结果(共 m m m个)投票表决出来的。
步骤是:

举个例子,现在有一个原始数据集有10个样本,他只有一维特征 x x x 和对应的标签 y y y,这个特征是连续的,取值从0.1到1.0,现在我们将基分类器都选择成决策树,自助样本集的数目定为5,也就是说我们要进行五组简单随机抽样。

用得到的五个决策树模型对所有样本做分类,然后对五次结果做Bagging

五轮投票结果完全正确分类了原始数据集的10个样本。样本最终的预测结果是根据基分类器的预测结果投票表决产生的(少数服从多数,取众数)。
4、Boosting(提升)
- Boosting由弱分类器得到强分类器的过程:迭代优化:样本加权系数、分类器加权系数;
- Boosting(提升):是一个迭代的过程,用来自适应的改变训练样本的分布,使分类器聚焦在那些很难分的样本上;
- Boosting(提升):是一个机器学习技术,可以用于回归和分类问题,它每一步产生个弱预测模型 (如决策树),并加权累到总模型中。如果每一步的弱预测生成都是依据损失函数的梯度方向,则称之为梯度提升(Gradient boosting);
- 梯度提升(Gradient boosting)算法:首先给定 一个目标损失函数,它的定义域是所有可行的弱函数集合(基函数);提升算法通过迭代地选择一个负梯度方向上的基函数来逐渐逼近局部极小值 。这种在函数域的梯度提升观点对机器学习的很多领域有深刻影响;
- Boosting(提升)的理论意义:如果一个问题存在弱分类器,则可以通过提升的办法得到强分类器;
- 以决策树(分类树、回归树)为基学习器的提升(boosting)方法称为提升树(Boosting tree)。
- 对于Boosting,每一步我们都会在上一轮的基础上更加拟合原数据,总体上实现了整体模型的偏差(bias)最小化。所以对于每个基分类器来说,首要任务就是如何降低方差(variance),即选择更简单的分类器,所以我们采用深度很浅的决策树。
Boosting(提升)算法
- 给定输入向量 x \textbf{x} x 和输出变量 y y y 组成的若干训练样本 ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) (\textbf{x}_1,y_1),(\textbf{x}_2,y_2),…,(\textbf{x}_n,y_n) (x1,y1),(x2,y2),…,(xn,yn),目标是找到近似函数 F ^ ( x ) \hat{F}(\textbf{x}) F^(x),使得损失函数 L ( y , F ^ ( x ) ) L(\textbf{y},\hat{F}(\textbf{x})) L(y,F^(x)) 最小。
- 损失函数 L ( y , F ^ ( x ) ) L(\textbf{y},\hat{F}(\textbf{x})) L(y,F^(x)) 的典型定义:
- 均方差损失: L ( y , F ^ ( x ) ) = ∑ i = 1 n ( y i − F ^ ( x i ) ) 2 L(\textbf{y},\hat{F}(\textbf{x}))=\sum^n_{i=1}(\textbf{y}_i-\hat{F}(\textbf{x}_i))^2 L(y,F^(x))=∑i=1n(yi−F^(xi))2;平均值是均方差函数极小值的最优解
- 绝对值损失: L ( y , F ^ ( x ) ) = ∑ i = 1 n ∣ y i − F ^ ( x i ) ∣ L(\textbf{y},\hat{F}(\textbf{x}))=\sum^n_{i=1}|\textbf{y}_i-\hat{F}(\textbf{x}_i)| L(y,F^(x))=∑i=1n∣yi−F^(xi)∣;中位数是绝对值函数极小值的最优解
5、Bagging和Boosting的区别
-
样本选择上:
- Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
- Boosting(Adaboost):Adaboost每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化,权值是根据上一轮的分类结果进行调整。
- Boosting(GBDT):GBDT每次迭代都使用所有样本。
-
样例权重:
- Bagging:使用均匀取样,每个样例的权重相等
- Boosting(Adaboost):根据错误率不断调整样例的权值,错误率越大则权重越大。
- Boosting(GBDT):GBDT每次迭代所有样本权重都一样,而且最终的GBDT强学习器是所有 T T T 次迭代得到的 T T T 个弱分类器的加和。
-
预测函数:
- Bagging:所有预测函数的权重相等。
- Boosting(Adaboost):每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。
- Boosting(GBDT):最终的GBDT强学习器是所有 T T T 次迭代得到的 T T T 个弱分类器的加和。
-
并行计算:
- Bagging:各个预测函数可以并行生成
- Boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。
四、Stacking堆叠法
Stacking方法是指训练一个模型用于组合其他各个模型。把个体学习器称为初级学习器,把用于结合的学习器称为次级学习器。
首先从初始数据集训练初级学习器,然后把之前训练的各个模型的输出作为输入,用于训练次级学习器,以得到一个最终的输出。
初级学习器的输出被当做样例的输入特征,初始样本的标记仍作为样例标记。