图解机器学习 | GBDT模型详解
作者:韩信子@ShowMeAI
教程地址:http://www.showmeai.tech/tutorials/34
本文地址:http://www.showmeai.tech/article-detail/193
声明:版权所有,转载请联系平台与作者并注明出处
1.GBDT算法
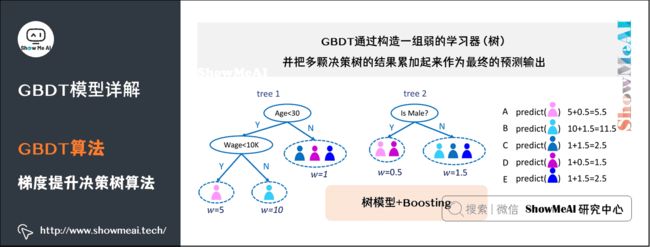
GBDT(Gradient Boosting Decision Tree),全名叫梯度提升决策树,是一种迭代的决策树算法,又叫 MART(Multiple Additive Regression Tree),它通过构造一组弱的学习器(树),并把多颗决策树的结果累加起来作为最终的预测输出。该算法将决策树与集成思想进行了有效的结合。
(本篇GBDT集成模型部分内容涉及到机器学习基础知识、决策树、回归树算法,没有先序知识储备的宝宝可以查看ShowMeAI的文章 图解机器学习 | 机器学习基础知识 、决策树模型详解 及 回归树模型详解)。
1)Boosting核心思想
Boosting方法训练基分类器时采用串行的方式,各个基分类器之间有依赖。它的基本思路是将基分类器层层叠加,每一层在训练的时候,对前一层基分类器分错的样本,给予更高的权重。测试时,根据各层分类器的结果的加权得到最终结果。
Bagging与Boosting的串行训练方式不同,Bagging方法在训练过程中,各基分类器之间无强依赖,可以进行并行训练。
2)GBDT详解
GBDT的原理很简单:
- 所有弱分类器的结果相加等于预测值。
- 每次都以当前预测为基准,下一个弱分类器去拟合误差函数对预测值的残差(预测值与真实值之间的误差)。
- GBDT的弱分类器使用的是树模型。
如图是一个非常简单的帮助理解的示例,我们用GBDT去预测年龄:
- 第一个弱分类器(第一棵树)预测一个年龄(如20岁),计算发现误差有10岁;
- 第二棵树预测拟合残差,预测值6,计算发现差距还有4岁;
- 第三棵树继续预测拟合残差,预测值3,发现差距只有1岁了;
- 第四课树用1岁拟合剩下的残差,完成。
最终,四棵树的结论加起来,得到30岁这个标注答案(实际工程实现里,GBDT是计算负梯度,用负梯度近似残差)。
(1)GBDT与负梯度近似残差
回归任务下,GBDT在每一轮的迭代时对每个样本都会有一个预测值,此时的损失函数为均方差损失函数:
l ( y i , y i ^ ) = 1 2 ( y i − y i ^ ) 2 l(y_{i}, \hat{y_{i}})=\frac{1}{2}(y_{i}-\hat{y_{i}})^{2} l(yi,yi^)=21(yi−yi^)2
损失函数的负梯度计算如下:
− [ ∂ l ( y i , y i ^ ) ∂ y i ^ ] = ( y i − y i ^ ) -[\frac{\partial l(y_{i}, \hat{y_{i}})}{\partial \hat{y_{i}}}]=(y_{i}-\hat{y_{i}}) −[∂yi^∂l(yi,yi^)]=(yi−yi^)
可以看出,当损失函数选用「均方误差损失」时,每一次拟合的值就是(真实值-预测值),即残差。
(2)GBDT训练过程
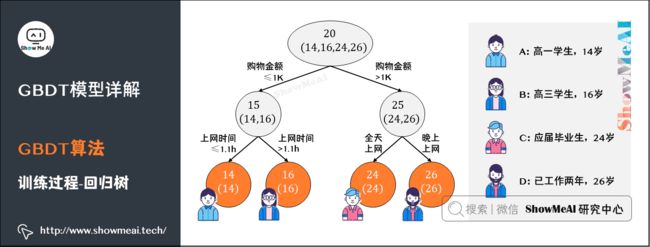
我们来借助1个简单的例子理解一下GBDT的训练过程。假定训练集只有4个人 (A,B,C,D),他们的年龄分别是 (14,16,24,26)。其中,A、B分别是高一和高三学生;C、D分别是应届毕业生和工作两年的员工。
我们先看看用回归树来训练,得到的结果如下图所示:
接下来改用GBDT来训练。由于样本数据少,我们限定叶子节点最多为2(即每棵树都只有一个分枝),并且限定树的棵树为2。最终训练得到的结果如下图所示:
上图中的树很好理解:A、B年龄较为相近,C、D年龄较为相近,被分为左右两支,每支用平均年龄作为预测值。
-
我们计算残差(即「实际值」-「预测值」),所以A的残差14-15=-1。
-
这里A的「预测值」是指前面所有树预测结果累加的和,在当前情形下前序只有一棵树,所以直接是15,其他多树的复杂场景下需要累加计算作为A的预测值。
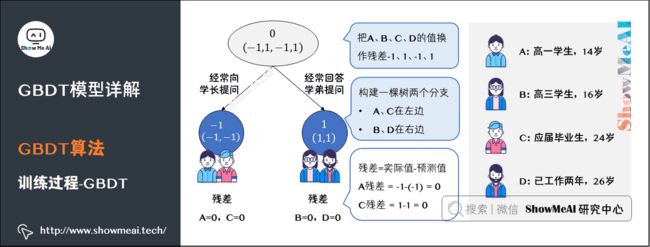
上图中的树就是残差学习的过程了:
-
把A、B、C、D的值换作残差-1、1、-1、1,再构建一棵树学习,这棵树只有两个值1和-1,直接分成两个节点:A、C在左边,B、D在右边。
-
这棵树学习残差,在我们当前这个简单的场景下,已经能保证预测值和实际值(上一轮残差)相等了。
-
我们把这棵树的预测值累加到第一棵树上的预测结果上,就能得到真实年龄,这个简单例子中每个人都完美匹配,得到了真实的预测值。
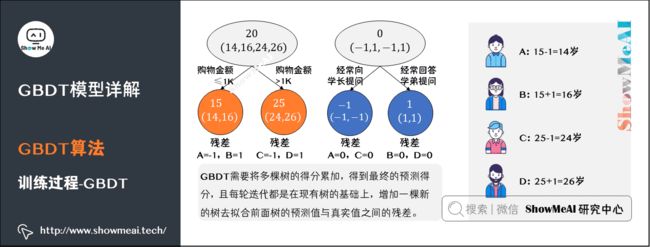
最终的预测过程是这样的:
- A:高一学生,购物较少,经常问学长问题,真实年龄14岁,预测年龄A = 15 – 1 = 14
- B:高三学生,购物较少,经常被学弟提问,真实年龄16岁,预测年龄B = 15 + 1 = 16
- C:应届毕业生,购物较多,经常问学长问题,真实年龄24岁,预测年龄C = 25 – 1 = 24
- D:工作两年员工,购物较多,经常被学弟提问,真实年龄26岁,预测年龄D = 25 + 1 = 26
综上,GBDT需要将多棵树的得分累加得到最终的预测得分,且每轮迭代,都是在现有树的基础上,增加一棵新的树去拟合前面树的预测值与真实值之间的残差。
2.梯度提升 vs 梯度下降
下面我们来对比一下「梯度提升」与「梯度下降」。这两种迭代优化算法,都是在每1轮迭代中,利用损失函数负梯度方向的信息,更新当前模型,只不过:
-
梯度下降中,模型是以参数化形式表示,从而模型的更新等价于参数的更新。
-
梯度提升中,模型并不需要进行参数化表示,而是直接定义在函数空间中,从而大大扩展了可以使用的模型种类。
F = F t − 1 − ρ t ∇ F L ∣ F = F t − 1 F=F_{t-1}-\left.\rho_{t} \nabla_{F} L\right|_{F=F_{t-1}} F=Ft−1−ρt∇FL∣F=Ft−1
L = ∑ i l ( y i , F ( x i ) ) L=\sum_{i} l\left(y_{i}, F\left(x_{i}\right)\right) L=i∑l(yi,F(xi))
w t = w t − 1 − ρ t ∇ w L ∣ w = w t − 1 w_{t}=w_{t-1}-\left.\rho_{t} \nabla_{w} L\right|_{w=w_{t-1}} wt=wt−1−ρt∇wL∣w=wt−1
L = ∑ i l ( y i , f w ( w i ) ) L=\sum_{i} l\left(y_{i}, f_{w}\left(w_{i}\right)\right) L=i∑l(yi,fw(wi))
3.GBDT优缺点
下面我们来总结一下GBDT模型的优缺点:
1)优点
-
预测阶段,因为每棵树的结构都已确定,可并行化计算,计算速度快。
-
适用稠密数据,泛化能力和表达能力都不错,数据科学竞赛榜首常见模型。
-
可解释性不错,鲁棒性亦可,能够自动发现特征间的高阶关系。
2)缺点
-
GBDT在高维稀疏的数据集上,效率较差,且效果表现不如SVM或神经网络。
-
适合数值型特征,在NLP或文本特征上表现弱。
-
训练过程无法并行,工程加速只能体现在单颗树构建过程中。
4.随机森林 vs GBDT
对比ShowMeAI前面讲解的另外一个集成树模型算法随机森林,我们来看看GBDT和它的异同点。
1)相同点
-
都是集成模型,由多棵树组构成,最终的结果都是由多棵树一起决定。
-
RF和GBDT在使用CART树时,可以是分类树或者回归树。
2)不同点
-
训练过程中,随机森林的树可以并行生成,而GBDT只能串行生成。
-
随机森林的结果是多数表决表决的,而GBDT则是多棵树累加之。
-
随机森林对异常值不敏感,而GBDT对异常值比较敏感。
-
随机森林降低模型的方差,而GBDT是降低模型的偏差。
5.Python代码应用与模型可视化
下面是我们直接使用python机器学习工具库sklearn来对数据拟合和可视化的代码:
# 使用Sklearn调用GBDT模型拟合数据并可视化
import numpy as np
import pydotplus
from sklearn.ensemble import GradientBoostingRegressor
X = np.arange(1, 11).reshape(-1, 1)
y = np.array([5.16, 4.73, 5.95, 6.42, 6.88, 7.15, 8.95, 8.71, 9.50, 9.15])
gbdt = GradientBoostingRegressor(max_depth=4, criterion ='squared_error').fit(X, y)
from IPython.display import Image
from pydotplus import graph_from_dot_data
from sklearn.tree import export_graphviz
# 拟合训练5棵树
sub_tree = gbdt.estimators_[4, 0]
dot_data = export_graphviz(sub_tree, out_file=None, filled=True, rounded=True, special_characters=True, precision=2)
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())

ShowMeAI相关文章推荐
- 1.机器学习基础知识
- 2.模型评估方法与准则
- 3.KNN算法及其应用
- 4.逻辑回归算法详解
- 5.朴素贝叶斯算法详解
- 6.决策树模型详解
- 7.随机森林分类模型详解
- 8.回归树模型详解
- 9.GBDT模型详解
- 10.XGBoost模型最全解析
- 11.LightGBM模型详解
- 12.支持向量机模型详解
- 13.聚类算法详解
- 14.PCA降维算法详解
ShowMeAI系列教程推荐
- 图解Python编程:从入门到精通系列教程
- 图解数据分析:从入门到精通系列教程
- 图解AI数学基础:从入门到精通系列教程
- 图解大数据技术:从入门到精通系列教程
- 图解机器学习算法:从入门到精通系列教程