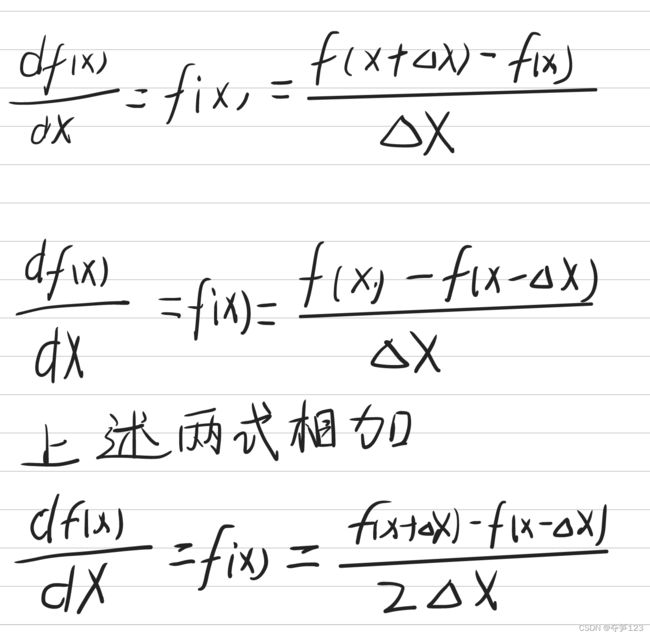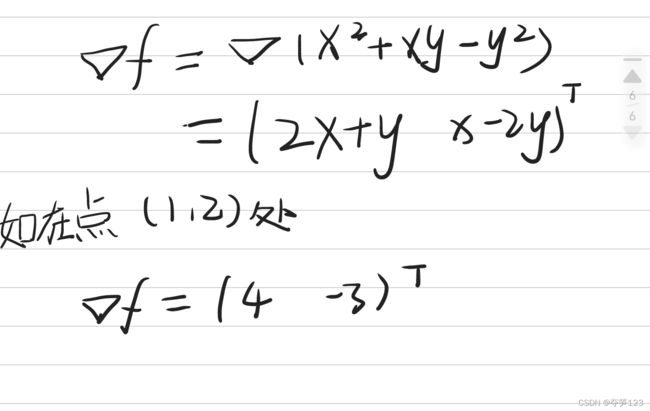从零到一实现神经网络：数学原理篇（一）

本博客参考书籍：深度学习入门（斋藤康毅著）

一元函数微积分

一阶导数

定义

函数自变量的变化值趋于0时，函数值的变化量与自变量变化量的比值，数学表达式为

数值微分的代码实现

使用代码实现

def numerical_diff(f,x):
	delta_x=1e-4
	return f(x+delta_x)/delta_x

利用微小差分求导数的过程称为数值微分，基于数学式的推导求导数的过程称为解析式求导

上述代码中存在的问题

上述代码中存在的问题，由于计算机存在数字的舍入误差（省略小数点后面精细部分而造成的误差，如省略小数点8位后的数字），所以delta_x不可能无限趋于0，这就导致定义与代码出现了矛盾——上述代码中实现的是（x+delta_x）与x之间的斜率（伪导数），而不是x处的斜率（真导数）

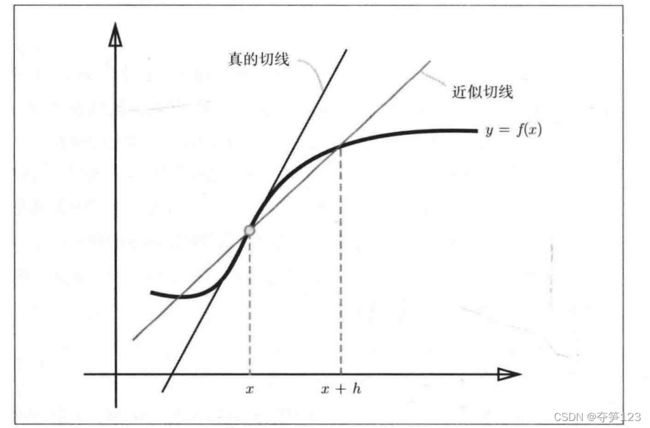
如何实现真正的导数用于表示函数在x处的斜率？
从导数定义出发，我们可以（x+delta_x）和（x-delta_x）之间的“伪导数”作为x处的“真导数”

数值微分代码改进

代码实现

def numerical_diff(f,x):
	delta_x=1e-4
	return (f(x+delta_x)-f(x-delta_x))/(2*delta_x)

导数的意义

导数的几何意义是函数在点（$x,f(x)$）处的斜率，反映了函数值在此点处变化的快慢（也可以说函数值沿着斜率的方向变化最快），下面我们使用代码生成函数$f(x)=0.1x^2+0.01x$在点$(5,f(5))和(10,f(10)$处的导数

import matplotlib.pyplot as plt
import numpy as np
def fun_1(x):
    return 0.1*x**2+0.01*x

def numerical_fun(f,x):
    h=1e-4
    return (f(x+h)-f(x-h))/(2*h)
def line(k,x):
    return k*x
x=np.arange(0.0,20.0,0.1)

y=fun_1(x)
y1=line(numerical_fun(fun_1,5),x)
y2=line(numerical_fun(fun_1,14),x)

plt.xlabel('x')
plt.ylabel('f(x)')
plt.plot(x,y)
plt.plot(x,y1-fun_1(5.0),'--')
plt.plot(x,y2-fun_1(14.0),'--')
plt.show()

多元函数微积分

偏导数

定义

导数是一元函数的变化值与自变量的变化值比值的极限，多元函数有多个自变量，每个自变量都会发生变化，情况更加复杂

偏导数是多元函数对各个自变量的导数，是一元函数的推广，多元函数$f(x)$关于自变量$x_i$的偏导数$f^{{}^{\prime }}(x_i)$的数学表达式为

求多元函数关于某个自变量的偏导数时，将其他自变量看作常数项

偏导数代码实现

多元函数的梯度包含了函数关于所有自变量的偏导数，因此该部分代码请往下看：
梯度的代码实现

偏导数的意义

例如下面的图片中，我们将纵轴Z看作函数值，X,Y轴看作自变量，在某一点求得Z关于Y的偏导数，做出图形：是一个长方形（因为此时自变量X被视为常数，沿着长方形平面方向，X值不变）

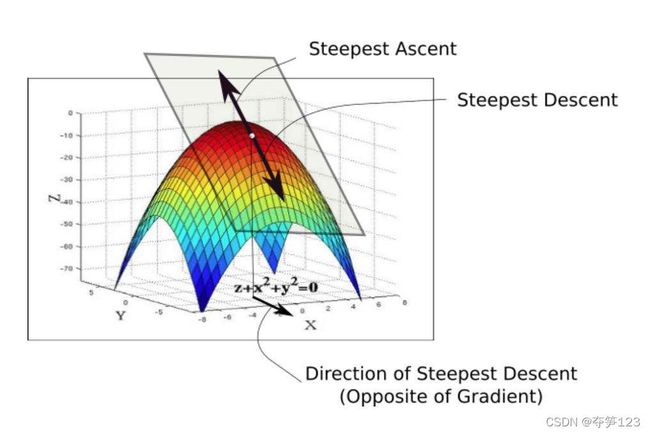
沿着垂直于Y轴的方向看去，得到一个关于Y和Z的二维平面

如此我们会看到偏导数的导数的相似之处，函数关于某个自变量的偏导数是函数值在该变量方向上变化最快的方向

梯度

一阶偏导数只对一个自变量求导数，它反映了多元函数与一个自变量之间的关系，梯度则包含了函数对所有自变量的偏导数，综合反映了函数值与所有自变量之间的关系

梯度是一个向量，里面的每个元素都是函数关于各个自变量的偏导数。从上面的图片中我们可以想到，如果在代码中，想要求一个多元函数的梯度，只需要依次求该函数关于每个自变量的偏导数，然后将这些偏导数放在一个numpy数组中即可

梯度的代码实现

def numerical_grad(f,x):	
	'''x:函数f的自变量，通常是一个数组'''
	h=1e-4
	grad=np.zeros_like(x)	# 生成一个形状与x相同的数组，元素都是0
	
	for i in range(x.size):
		tmp=x[i]
		# 求f(x+h)
		x[i]=tmp+h	
		f1=f(x)		# 因为每次循环只是求函数关于自变量x[i]的偏导数，所以只有自变量x[i]发生改变，
		# 求f(x-h)
		x[i]=tmp-h
		f2=f(x)
		
		grad[i]=(f1-f2)/(2*h)	# 表示函数关于自变量x[i]的偏导数
		x[i]=tmp
	return grad	
'''关于求偏导能不能借用求导数的函数的问题
def numerical_fun(f,x):
    h=1e-4
    return (f(x+h)-f(x-h))/(2*h)
我们看到在上面求偏导的代码中每次循环实现的过程与求导数的代码极其相似，能不能借用呢？
不能够！我们可以看到，导数对应的函数是一元函数，只有一个自变量，而偏导数对应的是多元函数，有多个自变量，求每个偏导数时，其他自变量都应该保持不变，而求导数的代码中没有满足该条件
'''	

求梯度的例子

对于函数$f(x,y)=x^2+xy-y^2$，它的偏导数为

梯度为

代码实现

在上面代码中笔者发现了一个小问题：自变量x的值类型竟然能够对结果的影响这么大，原因笔者还没有搞明白，有知道原因的小伙伴请赐教。不过在以后的学习过程中还是应该注意这方面的问题，感觉细节越来越多了

梯度的意义

梯度是一个包含了多元函数所有偏导数的向量，它反映的是各点处函数值变化最多的方向（图像上函数值改变最快的方向），在机器学习中我们要找的是函数值最小的方向

梯度法

如何求函数最值？

虽然梯度的方向不是函数最值所在的方向，但是沿着梯度的方向能够最大程度的改变函数的值，因此，寻找函数最小值的过程应该以梯度为线索

梯度法，函数值在当前位置沿着梯度方向前进一段距离，然后再新的地方继续求梯度，重复这个过程，直到梯度等于0

寻找函数最小值的梯度法称为梯度上升法，寻找函数最大值的梯度法称为梯度下降法，深度学习中大多使用梯度下降法

梯度下降法表达式

函数在某个自变量方向上的梯度更新

所谓的梯度下降，并不是梯度的减小，而是自变量沿着梯度的方向改变，最终求得函数取最小值时自变量的取值
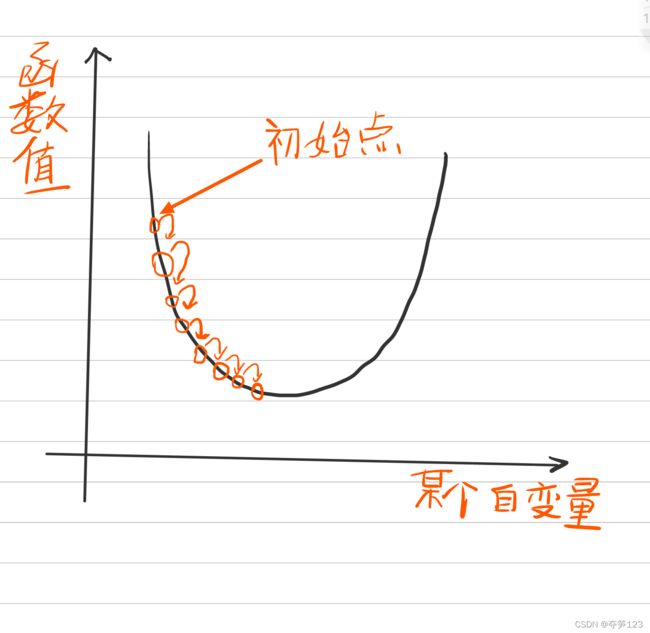
也许在这里你还会有一个疑问，凭什么要把初始点设置在那个位置，设置在别的地方可以吗？ 当然可以！实际上初始点的位置是随机的，上图只是一个自变量的初始点，如果是多个自变量的初始点，我们就得使用一个数组表示（见下面的利用梯度下降法求函数最值的例子）

梯度下降法图示过程

我们知道，梯度的意义是各点处函数值变化最快的方向，而负梯度的方向则是函数值减小最快的方向，在具有多个变量的空间中，函数值在多个变量上的梯度更新如图所示

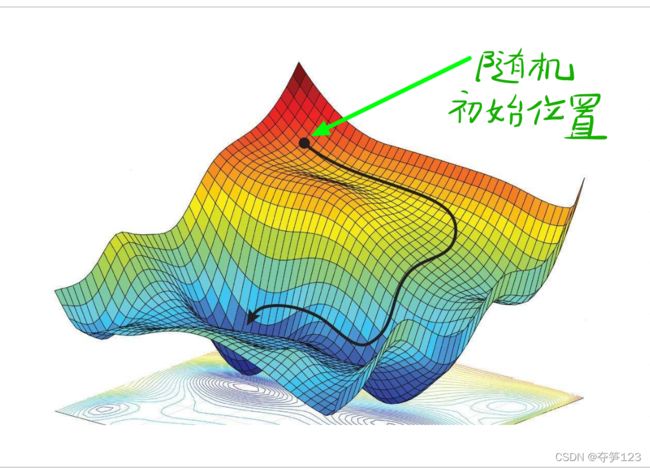
梯度下降法的代码实现

def grad_descent(f,init_x,lr=0.01,step_num=100):
	x=init_x
	for _ in range(step_num):	# step_num表示自变量x更新的次数
		grad=numerical_grad(f,x)	# 求梯度的函数
		x-=lr*grad	# 更新自变量，此时要求的是函数最小值，所以是负梯度方向
	return x		

如此我们便得到了，函数取得最小值时对应的自变量x=[x1,x2,…]（实际上要想得到真正的函数最小值，我们需要找到合适的学习率lr和自变量更新次数step_num），在神经网络中，函数通常指的是损失函数，而自变量通常指的是权重参数
我们在从零到一实现神经网络（python）:四中将举例介绍，利用梯度下降法求损失函数取得最小值时对应的权重参数

利用梯度下降法求多元函数最小值的例子

假设要求函数$f(x,y,z)=2(x-1{)}^2+(y-0.5{)}^2+(z+4{)}^2$的最小值，下面我们通过代码实现

def fun_1(x):
    return 2*(x[0]-1)**2+(x[1]-0.5)**2+(x[2]+4)**2

x=np.array([10.0,10.0,10.0])	# 随机初始自变量的值
a=grad_descent(fun_1,x,step_num=500)
print(a)	

代码运行结果

在这个激动人心的时刻！显而易见，我们通过对二次函数性质的了解就知道，这个函数取得最小值时，一定在点（1,0.5,-4）处，而计算机帮我们实现了这一过程！

在上面的代码中，自变量的值是随机设置的，但是经过梯度下降法，我们得到了想要的坐标点！实际上，在神经网络中，我们将会随机设置权重参数的值，然后经过梯度下降法，求得损失函数取得最小值时对应的那组权重参数。