神经网络的反向传播算法推导

目录

一、定义

二、神经网络结构图

三、反向传播算法的四个公式推导

---

        有了上一篇  神经网络的反向传播算法推导 — 前期知识准备  做铺垫，下一步来看看反向传播算法具体的推导过程。

一、定义

机器学习中常说的两个函数：

损失函数 (loss function)：是定义在单个样本上的，算的是一个样本的值和预测值的误差，记为C(Θ)；

代价函数 (cost function)：是定义在整个训练集上的，是所有样本误差的平均，也就是损失函数的平均，记为J(Θ)；

假设函数：

[变量定义]

 : 表示神经网络第 l 层神经元的个数

：表示神经网络最终输出的类别数（L表示最后一层）

i： 的尺寸/维度的列，第 i 列

j： 的尺寸/维度的行，第 j 行

二、神经网络结构图

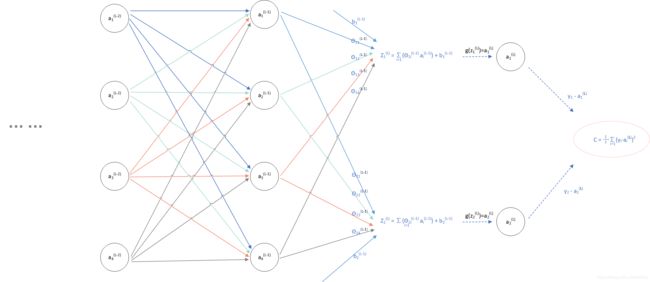
以三层神经网络为例：

                                                                （图1）

上图按照神经网络的计算方法（如不清楚的请参考文章 从逻辑回归到神经网络）：

                                                                （图2）

说明：图2中将  、 标为”常量“，有些欠妥，总之意思就是与  无关。

在计算图中可表示如下（ 损失函数计算方式有多种，假设我们使用最小化误差函数       ）：

这里为什么不是平方误差损失函数    ，我的理解是在神经网络在计算损失函数时 i 从1到 n对应的是一个样本的多个特征属性，而不是多个样本，因此无需求和后除以m.

三、反向传播算法的四个公式推导

先抛出反向传播算法的四个公式：

           -------------------- BP1

   ------------------- BP2 

  -------------------------------------- BP3

  ---------------------------------- BP4

（说明：其中，

BP2有的定义为：   

BP3有的定义为：

BP4有的定义为：

主要是层数 l 的定义不同，和变量命名不同，本质一样的。

)

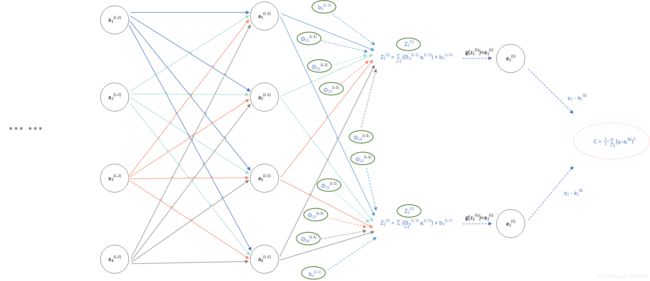
下面用计算图的方式逐一推导（依然以三层神经网络开头）：

 

                                                              （图3）

由三层神经网络推广到L层，我们从L-1层开始计算，则计算图如下：

                                                                （图4）

为了方便对图中路径进行求导（计算权重），所以补充了节点虚线，类似如下：

                                                                （图5）

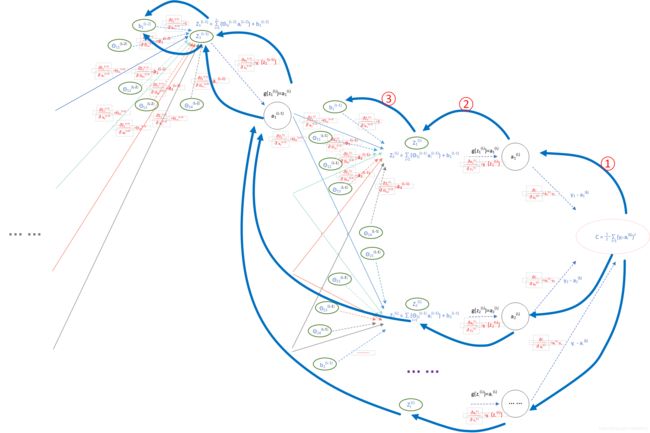
下一步开始对每条路径求偏导：

                                                                （图6）

        根据上一篇  神经网络的反向传播算法推导 — 前期知识准备  求导的反向模式求导：求损失函数C关于某一节点的偏导数，只需要把该节点每条反向路径上的偏导数做乘积，再求和即可。到此，我们已经在计算图上求得损失函数C关于模型参数的偏导数    、  ，而反向传播算法就是在此基础上通过定义一个损失/误差：   ，先逐层向后传播得到每一层节点的损失    ，再通过每一个节点的损失    来求解该节点的    、  ，计算步骤：

第一步：令损失函数C关于第 l 层的第 j 个元素的偏导为：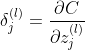

第二步：计算最后一层    

                                                                （图7）

        按照反向模式求导，节点 C 到  的反向路径只有一条，例如：上图中 C 到  的路径为① -> ② ，按照”同一可达路径相乘，不同可达路径相加“的原则：

                                                                （图8）

【说明】▽的物理意义：▽为对矢量做偏导,它是一个矢量，▽U表示为矢量U的梯度；

其中  的操作是把两个向量对应元素相乘组成新的元素。

图8即为反向传播算法公式 BP1：     

图7中（紫色路径） C 节点到  的反向路径有条，按照“同一可达路径相乘，不同可达路径相加”的原则：

...

...

其中     ——>  ，所以，提取公共部分，并且向量化、得到：

  

推广到 l 层：   即反向传播算法公式 BP2

说明：有的定义 BP2 为   ，这应该是层数 l 的定义不同， 相当于 ，本文延续斯坦福大学机器学习教程中的定义 、

接下来计算   

                                                                （图9）

图9中 节点C到节点  的反路径为 ① -> ② -> ③ 

...

...

由此，得到反向传播算法公式 BP3   

最后计算  

                                                                （图9）

图9中 节点C到节点  的反路径为 ① -> ② -> ③ 

...

由此，得到反向传播算法公式 BP4   

到此，神经网络的反向传播算法的四个公式推导结束。