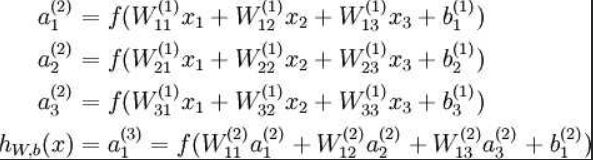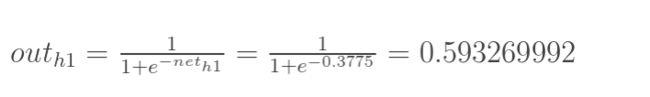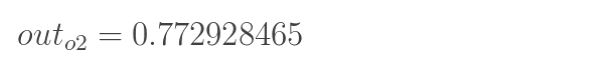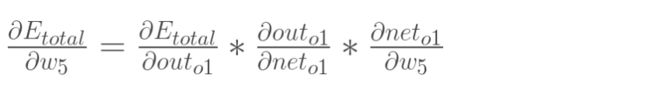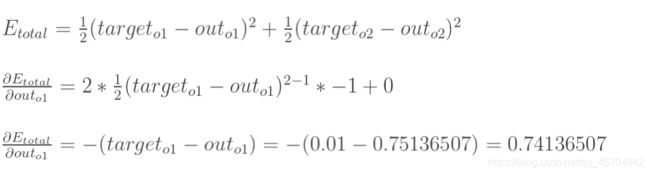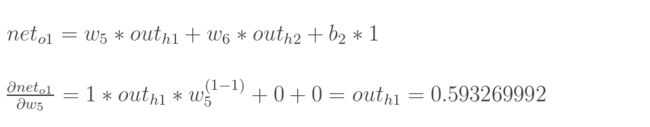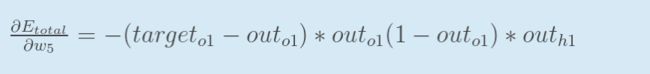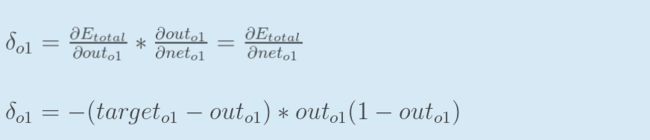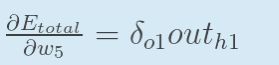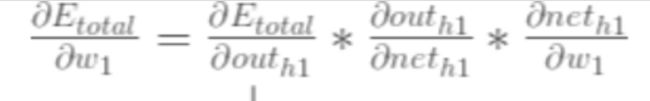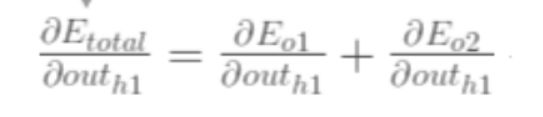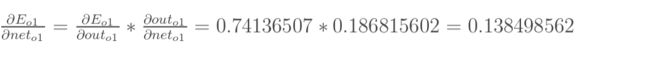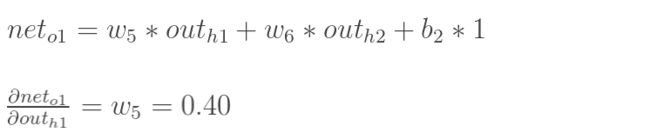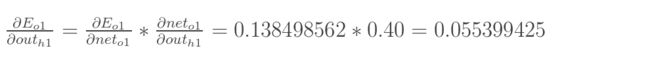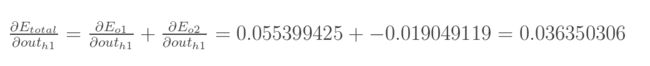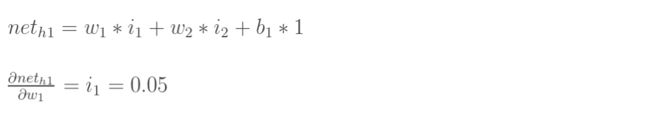顶着一坨数学公式耐心弄懂神经网络基础中的反向传播法
相信我 耐心看完 肯定能懂的！
参考了几个大佬的文章
然后做了个简单的整理和结合
一文弄懂神经网络中的反向传播法——BackPropagation
反向传播算法(Back propagation)
python 反向传播算法的入门教程的简单代码实现
文章目录
- 1.反向传播算法的简单理解
- 2.直观理解多层神经网络的训练
-
- 简单的三层神经网络
- 代入数值加深理解深层神经网络
-
- Step1 前向传播
-
- 1.输入层--->隐含层
- 2.隐含层--->输出层
- Step2 反向传播
-
- 0.先理解啥是反向传播！
-
- 梯度下降法
- 计算梯度
- 求多层复合函数所有变量的偏导数！
- 用BP算法求多层复合函数所有变量的偏导数！
- 1.计算总误差
- 2.误差是怎样反向传播的？
- 3.隐含层--->输出层的权值更新&计算过程（贼多公式警告！）
-
- 简化版公式！
- 4.隐含层--->隐含层的权值更新（贼多公式警告！）
-
- 简化版公式！
- 3.误差反向传播法小结
- 4.反向传播算法实现代码
1.反向传播算法的简单理解
反向传播算法是多层神经网络训练中举足轻重的算法
简单的理解：BP算法就是复合函数的链式法则，即对一个链式求导法则反复进行使用，但是BP算法在实际运算中的意义远大于链式法则。
想要理解BP算法 需要先直观理解多层神经网络的训练
2.直观理解多层神经网络的训练
首先，机器学习可以看做是数理统计的一个应用 数理统计中一个常见的任务就是拟合
拟合：给定一些样本点，用合适的曲线揭示这些样本点随自变量的变化关系。
深度学习同样是为了这个目的，不同的是 深度学习中样本点不再限定为(x,y)
而是可以由向量、矩阵等等组成的广义点对（X,Y）
广义点对之间的关系变得十分复杂，不太可能用一个简单函数表示。
然而，人们发现可以用多层神经网络来表示这样的关系
多层神经网络的本质就是一个多层复合的函数
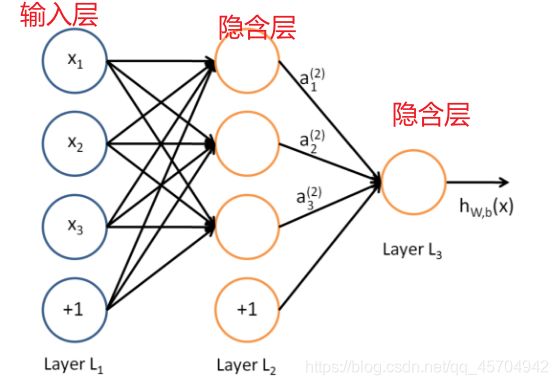
来看一个经典图
这是一个典型的三层神经网络的基本构成。
对应表达式如下：
wij就是相邻两层神经元之间的权值 即为深度学习需要学习的参数——也就相当于直线拟合y=kx+b中的待求参数k 和 b
现在我们手里有一些数据
输入：{x1，x2，x3，…，xn} 输出：{y1，y2，y3，…，yn}
我们深度神经网络是干啥的？
把输入数据在隐含层做某种变换 让输出数据与期望相同。
和直线拟合一样，深度学习的训练也有一个目标函数，这个目标函数定义了什么样的参数才算一组“好参数”，不过在机器学习中，一般是采用成本函数（cost
function），然后，训练目标就是通过调整每一个权值Wij来使得cost达到最小。 而这个成本函数cost
function也可以看成是由所有待求权值Wij为自变量的复合函数，而且基本上是非凸的（含有许多局部最小值）。
采用常用的梯度下降法可以有效地求解最小化cost函数的问题，从而训练出“好参数”。
接下来举一个例子 代入数值演示反向传播法的过程~
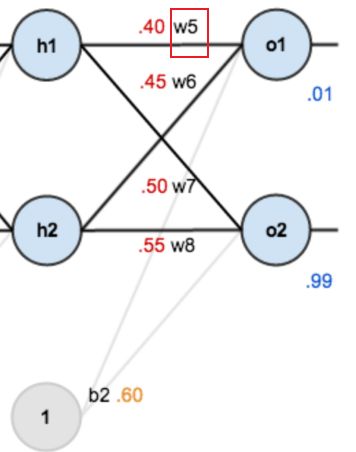
简单的三层神经网络
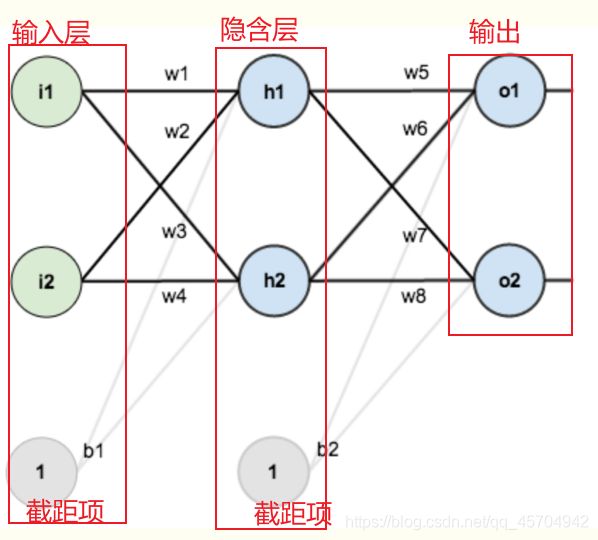
第一层是输入层 包含两个神经元i1 i2 截距项b1
第二层是隐含层
第三层是输出o1 o2
每条线上标的wi是层与层之间连接的权重
激活函数是我们默认的sigmoid函数
代入数值加深理解深层神经网络
现在来给这些权重、输入数据、输出数据赋一个值
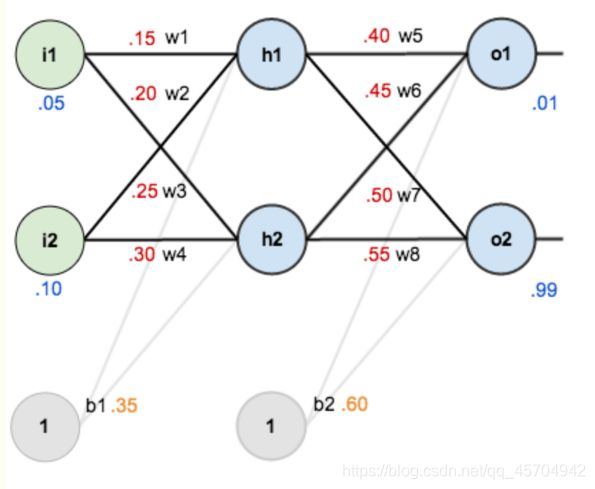
输入数据 i1=0.05 i2=0.10
输出数据o1=0.01 o2=0.99
初始权重 w1=0.15 w2=0.20 w3=0.25 w4=0.30
w5=0.40 w6=0.45 w7=0.50 w8=0.55
目标：给出输入数据i1 i2 使输出尽可能与原始输出o1 o2 接近
为了实现这个目标 我们要经历怎么样一个过程呢？
Step1 前向传播
1.输入层—>隐含层
计算隐藏层神经元h1的输入加权和：
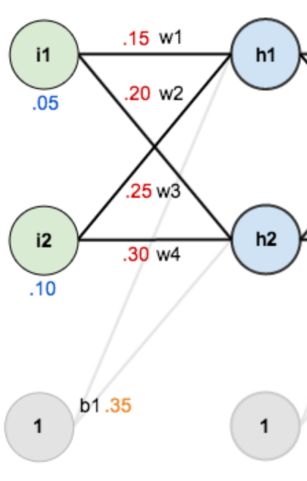
neta代表结点a的输入值
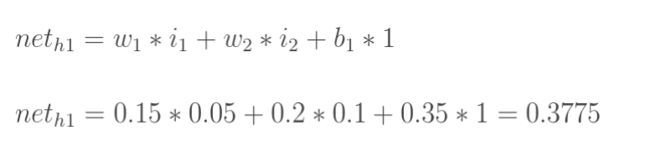
神经元h1的输出o1：（此处用到激活函数为sigmoid函数）
同理 可以计算出同层的神经元h2的输出o2：
2.隐含层—>输出层
计算输出层神经元o1和o2的值：
同理 o2值为
前向传播过程结束！
得到了输出值o1 o2 ： [0.75136079 , 0.772928465]
实际值是：[0.01,0.99]…所以还差挺远呐
但是没关系啊
我们对误差进行反向传播，更新权值，重新计算输出
Step2 反向传播
0.先理解啥是反向传播！
【1】明确我们的最终目标——通过训练获得 Wij 参数
【2】怎么训练？——通过调整每一个权值Wij来使得cost函数（成本函数）达到最小
这里cost函数也可以看成是由所有待求权值Wij为自变量的复合函数
cost函数基本上是非凸的 即含有许多局部最小值
【3】如何调整Wij 来求解最小化cost函数的问题？——使用梯度下降法
梯度下降法
给定一个初始点 并 求出初始点的梯度向量
然后以负梯度方向为搜索方向 以一定的步长进行搜索
从而确定下一个迭代点 再计算这个新的梯度方向
重复以上步骤直到cost函数收敛
计算梯度
重点来啦！
之前我一直不知道为啥子要有——
整体误差对w5的偏导值来代表权重w5对整体误差产生了多少影响
这一步
现在来看一下！
之前说
所以假设cost函数为 H(W11,W12,…,Wij,…,Wmn) 那么它的梯度向量[2]就等于——
其中eij表示正交单位向量
为此 我们需要求出cost函数H对每一个权值Wij的偏导数
这！就引出了我们的BP算法~
我们要用BP算法来求解这种多层复合函数（指cost函数）的所有变量（W11 W12 …）的偏导数
求多层复合函数所有变量的偏导数！
举个栗子来说明~~
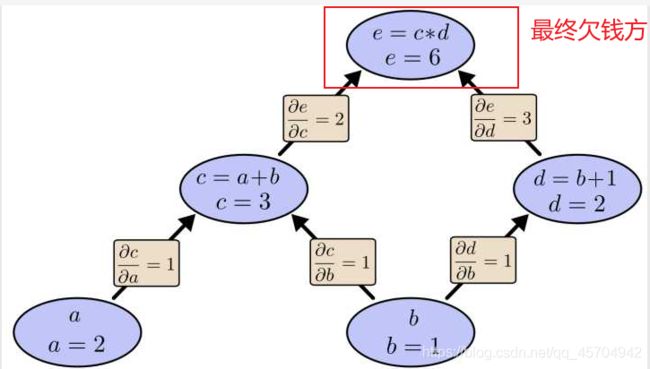
求e=(a+b)*(b+1)的偏导
可以看到图中引入了中间变量 c d
代入数值进行计算
为了求a=2 b=1时 e的梯度——
可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系
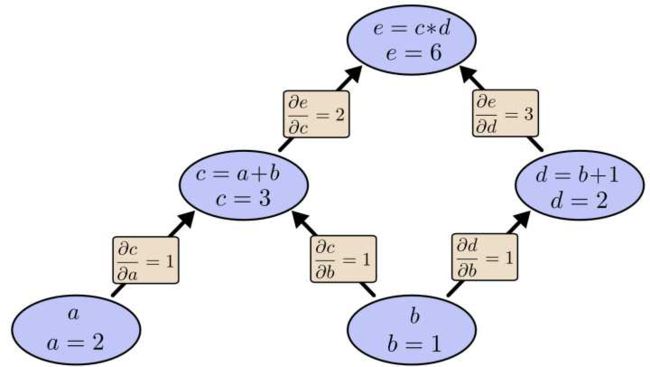
由链式法则我们知道
这里
全文最香的知识点中之一就被自然而然地引出来了！！
之前学链式法则 也没想太多 现在看到这里的应用 可以看出来：
e（上层节点）对a（下层节点）求偏导的值=从a到e的路径上的所有偏导值的乘积
e对b求偏导的值=从b到e的路径上（分别为 b-c-e b-d-e）的所有偏导值的乘积
这样做是十分冗余的！因为许多路径被重复访问！
例如上图中的 a-c-e b-c-e就都走了路径c-e
对于权值Wij动辄数万的深度模型中的神经网络 此种冗余会导致极大的计算量！
所以 我们要——
用BP算法求多层复合函数所有变量的偏导数！
同样利用链式法则 反向传播算法机智地避开了这种冗余
BP算法对每一个路径只访问一次就能求顶点对所有下层节点的偏导值
反向传播算法是反向（自上而下）来寻找路径的！
举个不太恰当的例子，如果把上图中的箭头表示欠钱的关系，即c→e表示e欠c的钱。
以a, b为例，直接计算e对它们俩的偏导相当于a,b各自去讨薪。
a向c讨薪，c说e欠我钱，你向他要。于是a又跨过c去找e。b先向c讨薪，同样又转向e，b又向d讨薪，再次转向e。可以看到，追款之路，充满艰辛，而且还有重复，即a,b 都从c转向e。而BP算法就是e主动还款。e把所欠之钱还给c，d。 c，d收到钱，乐呵地把钱转发给了a，b，皆大欢喜。
反向操作 芜湖 很高效！
1.计算总误差
总误差：(square error)
但是有两个输出 所以分别计算o1和o2的误差
总误差=o1误差+o2误差
o1误差为 1/2*(o1实际目标值 - o1真实输出值)
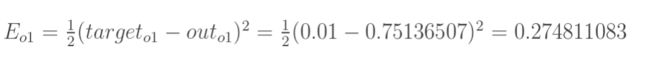
同理 o2误差为
总误差：
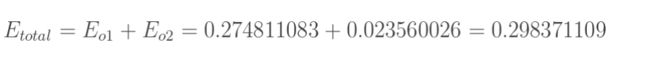
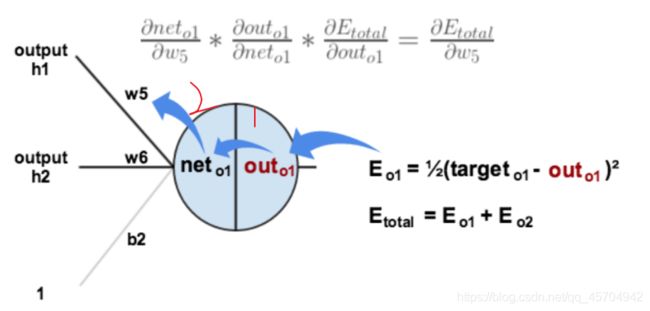
2.误差是怎样反向传播的？
放一张图更直观地看出误差是怎样反向传播的：
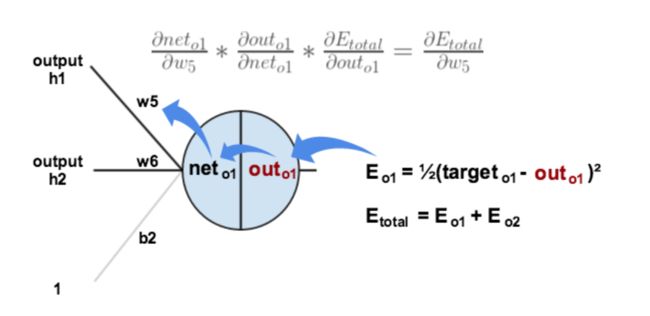
可以看到
误差o1->o1输出->o1输入->权重w5
确实是“反向”传播嘛！
3.隐含层—>输出层的权值更新&计算过程（贼多公式警告！）
超多公式警告！
时间不充裕 或者 懒得看原理的 直接划到最下面康康代码也挺好~
以权重参数w5为例
如果我们想知道权重w5对整体误差产生了多少影响 可以用整体误差对w5求偏导——
注意这里利用了链式法则
分别计算其中的三个偏导
【1】总误差对输出值o1的偏导：
【2】输出值o1对输入值o1的偏导（实际就是sigmoid函数求导嗷！）
【3】输入值o1对权重w5的偏导
三者相乘——得到结果（代表了权重w5对总误差产生的影响）：
即为总误差对权重w5的偏导值
简化版公式！
代入上面三个偏导的中间值 得出“总误差对权重w5的偏导值”的表达式：
用来表示输出层的误差——
即为总误差对输入值的偏导值
最后 将整体误差对w5的偏导公式整理为：输出层误差*输出值
ps:如果输出层误差记为负的话 也可以加个负号——写成：
最后来更新w5的值：
其中，是学习速率，这里我们取0.5
同理 可以更新 w6 w7 w8
4.隐含层—>隐含层的权值更新（贼多公式警告！）
超多公式警告！
时间不充裕 或者 懒得看原理的 直接划到最下面康康代码也挺好~
这部分的方法与上面的“隐含层—>输出层的权值更新”差不多
但是有个地方需要变一下——
在上文计算总误差对w5的偏导时
是从out(o1)---->net(o1)---->w5,
但是在隐含层—>隐含层之间的权值更新时
是out(h1)---->net(h1)---->w1
h1的输出值会接受o1 o2两个地方传来的误差 所以此处两个都要计算
老样子 链式法则走起~
就多注意下这个总误差对h1输出值的求偏导就行了
【1】总误差对h1输出值的偏导
先计算o1传到h1输出值的误差
对了 得先把o1输入值算出来 才能代入计算得到所求值
计算得到o1传到h1输出值的误差
同理：
o2传来的误差——
将两者相加得到第一个所求偏导
【2】h1的输出值对h1的输入值的偏导
【3】h1的输入值对权重w1的偏导
最后三者相乘 得到所求的
简化版公式！
为了简化公式，用σ(h1)表示隐含层单元h1的误差：
最后 更新w1的权重
同理 w2 w3 w4的权重更新——
3.误差反向传播法小结
看了这么多公式 有点乱不是
来做个小结：
通过隐含层-输出层 隐含层-隐含层对w1-w8这几个权重的更新完成一次迭代
之后再不断地进行迭代！直到得到误差最小的输出值 这个模型就算是训练好辽~
但是这么干说好不直观呐！那就上代码做一个迭代的展示好了~
4.反向传播算法实现代码
代码部分
这部分直接借鉴了博主的文章——
python 反向传播算法的入门教程的简单代码实现
#反向传播算法实现最小化cost（成本）函数
import numpy as np
i1=0.05#输入神经元1
i2=0.10#输入神经元2
b1=0.35#截距项1
b2=0.60#截距项2
w1=0.15
w2=0.20
w3=0.25
w4=0.30
w5=0.40
w6=0.45
w7=0.50
w8=0.55
target_o1=0.01
target_o2=0.99
learn_rate=0.5
#sigmoid函数的实现
def sigmoid(x):
return 1. / (1 + np.exp(-x))
net_h1=i1*w1+i2*w2+b1
net_h2=i1*w3+i2*w4+b1
out_h1=sigmoid(net_h1)
out_h2=sigmoid(net_h2)
net_o1=out_h1*w5+out_h2*w6+b2
net_o2=out_h1*w7+out_h2*w8+b2
out_o1=sigmoid(net_o1)
out_o2=sigmoid(net_o2)
print("初始输出：",out_o1,out_o2)
def E_total():
return (np.square(target_o1-out_o1)+np.square(target_o2-out_o2))*0.5
#输出层误差对权重的偏导
def Etotal_w5678(target,out_o,out_h):
return -(target-out_o)*out_o*(1-out_o)*out_h
#输出层误差
def E_out(target,out_o):
return -(target-out_o)*out_o*(1-out_o)
#隐含层-隐含层对权重的偏导
def Etotal_w1234(target_1,out_o1,w_ho1,target_2,out_o2,w_ho2,out_h,i):
return ((E_out(target_1,out_o1))*w_ho1+(E_out(target_2,out_o2))*w_ho2)*out_h*(1-out_h)*i
for i in range(160000):
# print(w1)
# print((E_out(target_o1,out_o1))*w5)
# print((E_out(target_o2,out_o2))*w7)
#对应分别是期望输出1，输出1，输出1和h1的权重，期望输出2，输出2，输出2和h1的权重，h1的输出，输入i1
w1=w1-learn_rate*Etotal_w1234(target_o1,out_o1,w5,target_o2,out_o2,w7,out_h1,i1)
#print(w1)
w2=w2-learn_rate*Etotal_w1234(target_o1,out_o1,w5,target_o2,out_o2,w7,out_h1,i2)
w3=w3-learn_rate*Etotal_w1234(target_o1,out_o1,w6,target_o2,out_o2,w8,out_h2,i1)
w4=w4-learn_rate*Etotal_w1234(target_o1,out_o1,w6,target_o2,out_o2,w8,out_h2,i2)
#print(w5)
w5=w5-learn_rate*Etotal_w5678(target_o1,out_o1,out_h1)
#print(w5)
w6=w6-learn_rate*Etotal_w5678(target_o1,out_o1,out_h2)
w7=w7-learn_rate*Etotal_w5678(target_o2,out_o2,out_h1)
w8=w8-learn_rate*Etotal_w5678(target_o2,out_o2,out_h2)
net_h1=i1*w1+i2*w2+b1
net_h2=i1*w3+i2*w4+b1
out_h1=sigmoid(net_h1)
out_h2=sigmoid(net_h2)
net_o1=out_h1*w5+out_h2*w6+b2
net_o2=out_h1*w7+out_h2*w8+b2
out_o1=sigmoid(net_o1)
out_o2=sigmoid(net_o2)
if(i%10000==0):
print("第{}次反向传播后，误差为{}".format(i,E_total()))
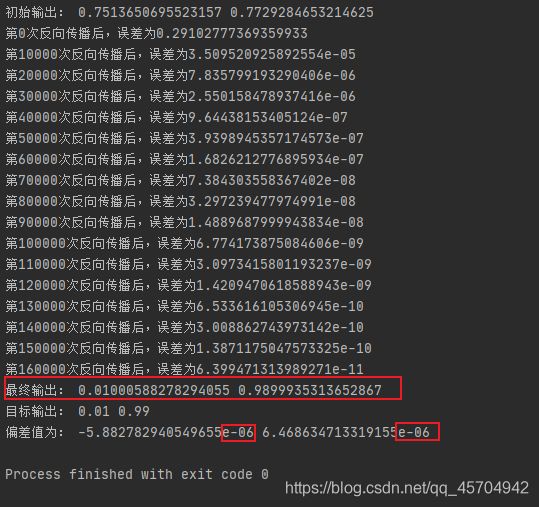
print("最终输出：",out_o1,out_o2)
print("目标输出：",target_o1,target_o2)
print("偏差值为：",target_o1-out_o1,target_o2-out_o2)
# print(w1)
# print(w2)
# print(w3)
# print(w4)
# print(w5)
# print(w6)
# print(w7)
# print(w8)
这里进行160000次迭代
可以看到我们进行16w次迭代之后
偏差值的量级已经变成了 10-6
很舒服啦！