基于MATLAB的数据插值运算:Lagrange与Hermite算法(附完整代码)
目录
一. Lagrange插值
1.1 数学解释
1.2 MATLAB实现
例题1
二. Hermite插值
2.1 数学解释
2.2 MATLAB实现
例题2
三. Runge现象
例题3
四. 分段插值
格式一
格式二
格式三
格式四
格式五
例题4
一. Lagrange插值
1.1 数学解释
对给定的n个插值点![]() ,可以构造n-1次Lagrange插值多项式。对插值区间内的任意x,对应的y值可由如下公式计算:
,可以构造n-1次Lagrange插值多项式。对插值区间内的任意x,对应的y值可由如下公式计算:
1.2 MATLAB实现
MATLAB中没有lagrange函数,需要提前自己构造。
构造函数代码如下:
function y=lagrange(x0,y0,x)
ii=1:length(x0);
y=zeros(size(x));
for i=ii
ij=find(ii~=i);
y1=1;
for j=1:length(ij),y1=y1.*(x-x0(ij(j)));
end
y=y+y1*y0(i)/prod(x0(i)-x0(ij));
end
end例题1
给定![]() 的部分数值表如下,用Lagrange插值法计算
的部分数值表如下,用Lagrange插值法计算![]() 的近似值。
的近似值。
| x | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| f(x) | -0.916291 | -0.693147 | -0.510826 | -0.356675 | -0.223144 |
解:
MATLAB代码如下:
clc;clear;
x=[0.4:0.1:0.8];
y=[-0.916291,-0.693147,-0.510826,-0.356675,-0.223144];
lagrange(x,y,0.54)
%函数部分
function y=lagrange(x0,y0,x)
ii=1:length(x0);
y=zeros(size(x));
for i=ii
ij=find(ii~=i);
y1=1;
for j=1:length(ij),y1=y1.*(x-x0(ij(j)));
end
y=y+y1*y0(i)/prod(x0(i)-x0(ij));
end
end运行结果如下:
ans =-0.6161
二. Hermite插值
2.1 数学解释
不少实际文体不仅要求在节点上函数值相等,还要求导数值也相等,甚至高阶导数值也相等,满足此种要求的插值多项式就是Hermite插值多项式。
已知n个插值点![]() ,以及对应的一阶导数值
,以及对应的一阶导数值![]() 。则对插值区间内任意x的函数值,对应y的Hermite插值公式如下:
。则对插值区间内任意x的函数值,对应y的Hermite插值公式如下:
上式子中的![]() 给定如下:
给定如下:
![]() 给定如下:
给定如下:
2.2 MATLAB实现
需要提前利用数学基础,自己构建hermite函数,相关代码如下:
function y=hermite(x0,y0,y1,x)
n=length(x0);
m=length(x);
for k=1:m
yy=0.0;
for i=1:n
h=1.0;
a=0.0;
for j=1:n
if j~=i
h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2;
a=1/(x0(i)-x0(j))+a;
end
end
yy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i));
end
y(k)=yy;
end
end例题2
给定如下数据,试构造Hermite多项式求出![]() 的近似值。并画图与标准值对比。
的近似值。并画图与标准值对比。
| 0.3 | 0.32 | 0.35 | |
| 0.29552 | 0.31457 | 0.34290 | |
| 0.95534 | 0.94924 | 0.93937 |
解:
MATLAB代码如下:
clc;clear;
x0=[0.3,0.32,0.35];
y0=[0.29552,0.31457,0.34290]; %函数值
y1=[0.95534,0.94924,0.93937]; %导数值
format long;
y=hermite(x0,y0,y1,0.34)
%画图
x=[0.3:0.005:0.35];
y=hermite(x0,y0,y1,x);
plot(x,y,'b') %蓝色为插值计算结果
y2=sin(x); %标准值
hold on
plot(x,y2,'r--') %红色为标准值
%函数部分
function y=hermite(x0,y0,y1,x)
n=length(x0);
m=length(x);
for k=1:m
yy=0.0;
for i=1:n
h=1.0;
a=0.0;
for j=1:n
if j~=i
h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2;
a=1/(x0(i)-x0(j))+a;
end
end
yy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i));
end
y(k)=yy;
end
end
运行结果:
y =0.333488890074074
三. Runge现象
根据区间[a,b]上给出的节点做插值多项式p(x)的近似值,一般总认为p(x)的次数越高则越逼近f(x)的精度,也就越好。但实际上并非如此。
典型的反例函数如下:
此函数在区间[-5,5]上的各阶导数均存在,但是在此区间上取n个节点所构成的Lagrange插值多项式在全区间内并非都是收敛的。可能这么说还难以理解,我们来看一个例子。
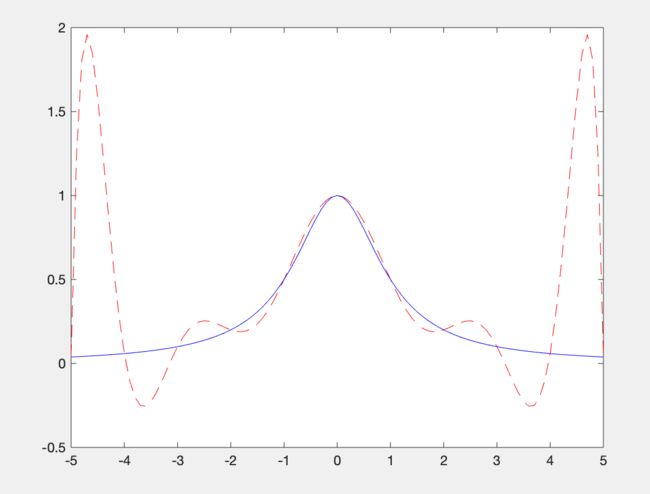
例题3
函数f(x)在区间[-5,5]上,取n=10,利用Lagrange插值法进行插值计算,并画图和标准值对比。函数f(x)定义如下:
解:
MATLAB代码如下:
clc;clear;
%插值计算
x=[-5:1:5];
y=1./(1+x.^2);
x0=[-5:0.1:5];
y0=lagrange(x,y,x0);
%标准值
y1=1./(1+x0.^2);
%绘图
plot(x0,y0,'--r') %红色代表插值
hold on
plot(x0,y1,'-b') %蓝色代表原曲线
%函数部分
function y=lagrange(x0,y0,x)
ii=1:length(x0);
y=zeros(size(x));
for i=ii
ij=find(ii~=i);
y1=1;
for j=1:length(ij),y1=y1.*(x-x0(ij(j)));
end
y=y+y1*y0(i)/prod(x0(i)-x0(ij));
end
end
运行结果:
可以发现该插值公式出现了较大误差。
四. 分段插值
分段插值可以解决Rung问题,所谓分段插值就是通过插值点用折线或低次曲线连接起来逼近原曲线。在MATLAB中,可以直接调用内部函数interp1()来实现。
该命令借助表格查找,对数据点之间计算内插值,从而找出一元函数f(x)在某个点的数值。该命令的常用格式有五种。
格式一
yi=interp1(x,Y,xi)
该命令返回插值向量yi,每一个元素对应于参量xi,同时由向量x和Y的内插值决定
格式二
yi=interp1(Y,xi)
假定x=1:N,其中N为向量Y的长度
格式三
yi=interp1(x,Y,xi,method)
该方法可用指定的算法计算插值。此处列举出五处常用的算法:
- 'nearest':最近邻点插值,可直接完成计算
- 'linear':线性插值,属于缺省方式,可直接完成计算
- 'spline':三次样条函数插值
- 'pchip'与cubic:分段三次Hermite插值
- 'v5cubic'与‘makima':修改后的Akima三次Hermite插值
备注:对于超出x范围的xi分量,使用nearest,linear,v5cubic插值算法会返回NaN;如果使用其他方法,interp1将对超出的分量执行外插值算法
格式四
yi=interp1(x,Y,method,'extrap')
格式五
yi=interp1(x,Y,method,extrapval)
确定超出x范围的xi中的分量的外插值extrapval,该值通常取NaN或者0
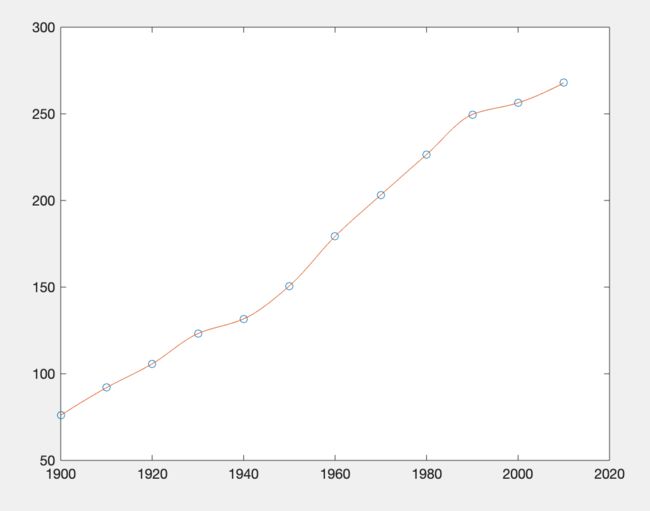
例题4
给定以下数据,计算1995年对应的product值,并将该插值计算的结果画图。
| year | 1900 | 1910 | 1920 | 1930 | 1940 | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 | 2010 |
| product | 75.995 | 91.972 | 105.711 | 123.203 | 131.669 | 150.697 | 179.323 | 203.212 | 226.505 | 249.633 | 256.344 | 267.893 |
解:
MATLAB代码如下:
clc;clear;
year=1900:10:2010;
product=[75.995,91.972,105.711,123.203,131.669,...
150.697,179.323,203.212,226.505,249.633,256.344,267.893];
p1995=interp1(year,product,1995) %单独计算1995年
%画图
x=1900:1:2010;
y=interp1(year,product,x,'PCHIP'); %使用三段三次Hermite插值的方法计算
plot(year,product,'o',x,y)
%实际值在图像中用圈圈表示运行结果:
p1995 = 2.529885000000000e+02
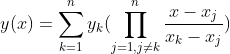
![y(x)=\sum_{i=1}^nh_i[(x_i-x)(2a_iy_i-y_i')+y_i]](http://img.e-com-net.com/image/info8/2d128e2c13fd45438758250124cba749.gif)