算法分析与设计期末总复习上（分治、动态规划，贪心部分）

							by--iamnii

这个是我期末考试自己做的总结，把书的重点内容基本梳理了一遍，但是有些上课没有讲的算法就没有归纳，大家可以结合自己老师讲的内容再深入复习。

另外，HNU算法考试基本都是算法思想、代码、应用、时间复杂度几个部分，所以总结的时候也是集中关注这几部分，希望对大家有帮助~

PS：有“应用”的部分一定要会画图或者打表，期中考试考过（活动安排问题之类的）的我就暂时没有总结，有时间再补充吧

分治法

1、基本思想：
将规模为n的问题分为k个规模较小的子问题。子问题和原问题相同且相互独立。递归地解决子问题并将子问题的解合并为原问题的解。一般而言，将问题分为大小相近的子问题是最有效率的。通常将问题一分为二。

2、算法复杂度（重点关注主定理）：

二分搜索

1、算法思想：

将n个元素分成个数大致相同的两半，取a[n/2]与x作比较，如果x= a[n/2]，则找到x，算法终止；如果x< a[n/2]，则只在数组左半部分继续搜索x；如果x> a[n/2]，则只在数组a的右半部分继续搜索x。

2、时间复杂度

3、代码

归并排序

1、算法思想：

递归：将待排序元素分成大小大致相同的两个子集合，分别对两个子集合进行排序，最终将排好序的子集合合并成所要求的排好序的集合。
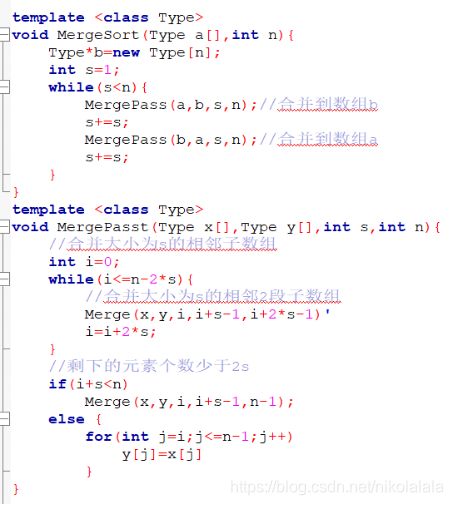
非递归：
首先将数组a中相邻元素两两配对，用合并算法将它们排序，构成n/2组长度为2的排好序的子数组段，然后再将它们排序成长度为4的排好序的子数组段，如此继续下去，直到整个数组排好序。

2、算法复杂度

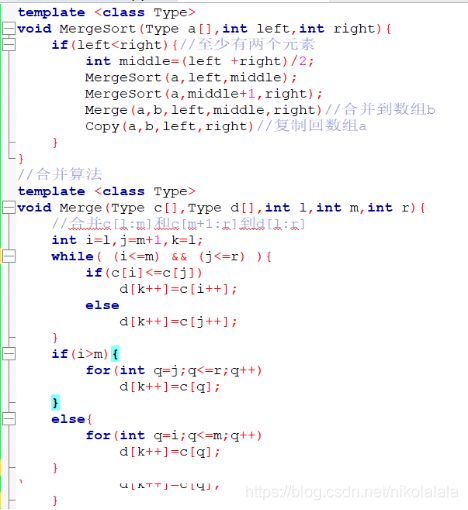
3、代码

（1）递归实现

（2）非递归

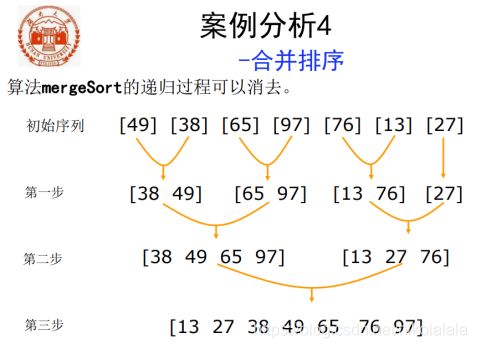
4、应用

快速排序

1、算法思想：

①分解（Divide)：以a[p]为基准元素将a[p:r]划分成3段alp:q-1]，a[q]和a[q+1:r]，使a[p:q-1]中任何一个元素小于等于a[q]，而 a[q+1:r]中任何一个元素大于等于a[q]，下标q在划分过程中确定。
②递归求解（Conquer）：通过递归调用快速排序算法，分别对a[p:q-1]和 a[q+1:r]进行排序。
③合并(Merge):由于对a[p:q-1]和a[q+1:r]的排序是就地进行的，因此在a[p:q-1]和a[q+1:r]都已排好的序后，不需要执行任何计算，a[p:r]则已排好序。

2、算法复杂度

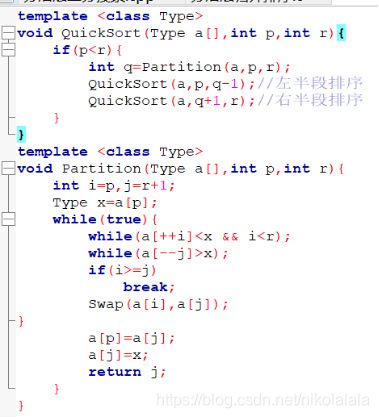
3、代码

大整数乘法

1、算法设计：
这个算法的式子和时间复杂度都要会自己推导，这部分内容比较集中，建议看书

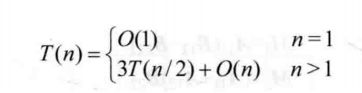
斯特拉森矩阵（了解）

动态规划

（简答题部分）
1、动态规划法定义：一种适用于解最优化问题，通过开辟一个空间存储子问题的最优解，在后续进行更新调用的解决多阶段决策问题的方法。

2、动态规划法指导思想：将待求解问题分解成若干子问题，在每种情况下，列出所有可能的局部解，并保存在表中，从局部解中挑出可能产生最佳结果的继续进行。

3、动态规划法步骤：
①找出最优解的性质，并刻画其结构特征；
②递归地定义最优值；
③以自底向上的方式计算最优值；
④根据计算最优值时得到的信息，构造最优解。

4、动态规划法基本要素：
①、最优子结构性质（原问题的最优解包含了其子问题的最优解）；
②、子问题重叠性质（当自顶向下递归解决问题时，每次产生的子问题不总是新问题，有些子问题被重复计算）。
动态规划法的核心是每个子问题只求解一次，将解保存在一个表格中

5. 分治法与动态规划的异同
主要共同点:
①、都要求原问题具有最优子结构性质；
②、都是将原问题分而治之，分解成若干个规模较小的子问题，然后将子问题的解合并，形成原问题的解；
主要区别:
①、子问题性质区别：分治法将分解后的子问题看成相互独立的；动态规划将分解后的子问题理解为相互间有联系，有子问题重叠性质；
③ 、实现方法区别：分治法通常利用递归自顶向下求解；动态规划通常利用迭代法自底向上求解，但也能用具有记忆功能的递归法自顶向下求解；

6.如何验证最优子结构特性
先写出问题的最优解和子问题的最优解的关系，然后假定问题的最优解成立（上面关系的左边成立），看能否得到子问题的最优解就是关系式右边的子问题最优解的形式，如果是就验证了最优子结构（一般用反证法）。

7、01背包问题之所以不能使用贪心算法而只能使用动态规划是因为01背包问题没办法装满整个背包，所以存在空间浪费，从而导致价值的改变。

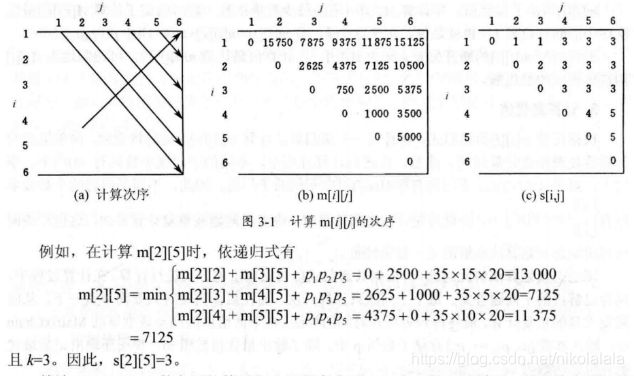
矩阵连乘问题（考应用可能大）

动态规划部分都一定要会写递推公式和打表应用

1、算法思想：

将矩阵连乘积AIAI+1…AJ记为A[I:J]，考察计算A[1:N]的最优计算次序，设这个计算次序在矩阵A[k]（1<=k

2、算法复杂度：

3、应用：

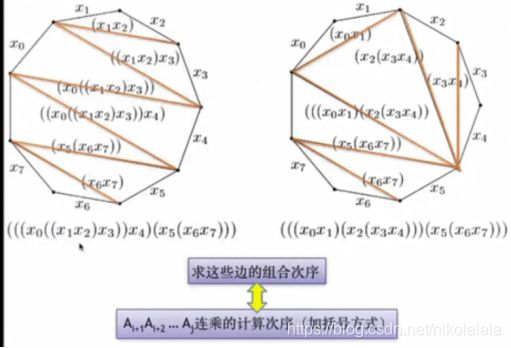
凸多边形最优三角剖分问题

1、算法思想：

2、时间复杂度：

占用空间为一个二维表，所以空间复杂度为O（n²），填格子需要n²的工作量，在每个格子内要n的时间找最小值，因此时间复杂度为O（n³）

3、代码(应该不会要求写)

4、应用

最长公共子序列问题

1、算法思想：

（1）最优子结构性质

（2）子问题的递归结构

2、时间复杂度

在所考虑的子问题空间，共有θ（mn）个不同的子问题，且每个数组单元的计算耗费O（1）的时间，因此算法LCSlength耗时O（mn）。

最大子段和问题

一、普通解法（略）

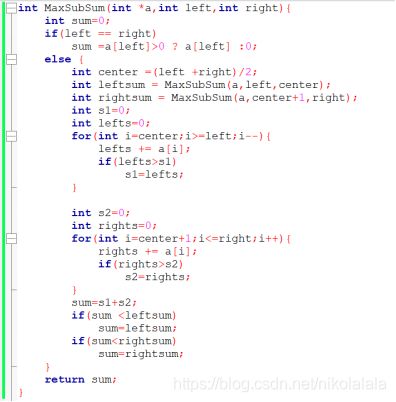
二、分治法

1、算法思想：

2、时间复杂度

3、代码

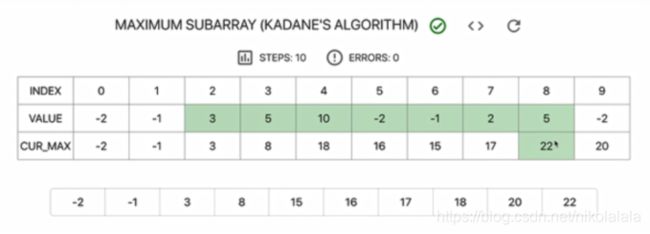
三、动态规划：

1、算法思想：

2、时间复杂度：

O（n）

3、代码

4、应用

贪心法

要求会证明谈心选择性质
1、性质：
**贪心选择性质（所求问题的整体最优解可以通过一系列局部最优选择得到）；
最优子结构性质。

2、与动态规划的区别：
①、动态规划算法通常以自底向上的方式解各子问题，而贪心算法则通常以自顶向下的方式进行
②、动态规划中的每步选择多依赖于相关子问题的解，因为只有解出相关子问题后才能做出选择；贪心算法中每步选择只需要局部最优，选择可依赖以前的选择，但不能依赖将来的选择，也不能依赖子问题的解
③、贪心算法的每一步直接对结果产生影响，动态规划不一定
④、贪心算法对每个子问题的解决方案都作出选择，不能回退；动态规划会根据以前的选择结果对当前进行选择，可以回退
⑤、动态规划只要运用于二维或三维，贪心一般是一维

3、基本思路：从问题的初始状态开始，每次找最优解，直到得到整个问题的最优解

4、证明贪心选择性质：先考察问题的一个整体最优解，并证明可以修改最优解顺序来满足贪心选择性质，即每次都取局部最优解，然后通过最优子结构性质进行证明，通过数学归纳法证明整个问题都有贪心选择性质

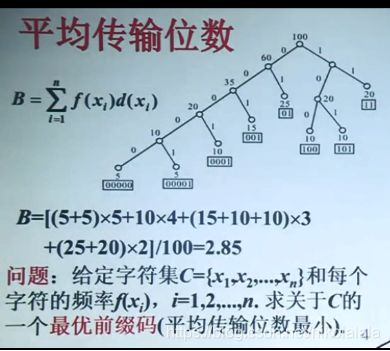
哈弗曼编码

平均传输位数概念：

1、算法思想：

2.时间复杂度

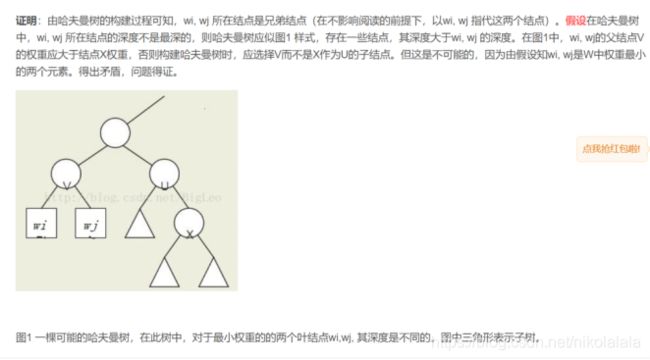
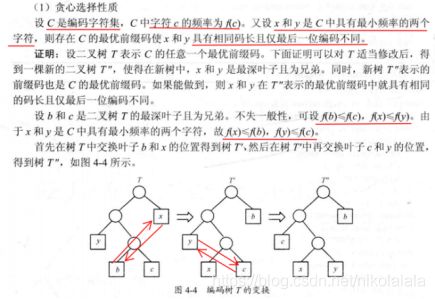
3、性质证明：

（1）、证明哈夫曼树最优

（2）、证明贪心选择性质

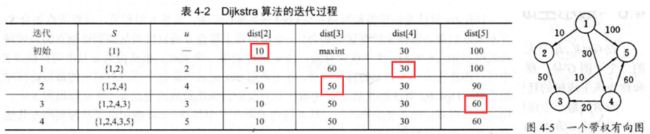
单源最短路径

1、算法思想

2、时间复杂度：

3、应用

4、性质证明

最小生成树

一、Prim算法

1、算法思想：

2、时间复杂度：O（n2）

二、Kruskal算法

1、算法思想

2、时间复杂度

多机调度问题

吐槽一下，这个算法老师上课其实也没有重点讲，但是期末考爆冷考了好几个类似的题。。。
1、算法思想：

2、时间复杂度

3、应用