Pytorch学习(六)—— 卷积神经网络ResNet
使用1*1的卷积核
- 1*1的卷积核给神经网络添加了一个非线性操作,从而减少或保持输入层中的信道数量保持不变。
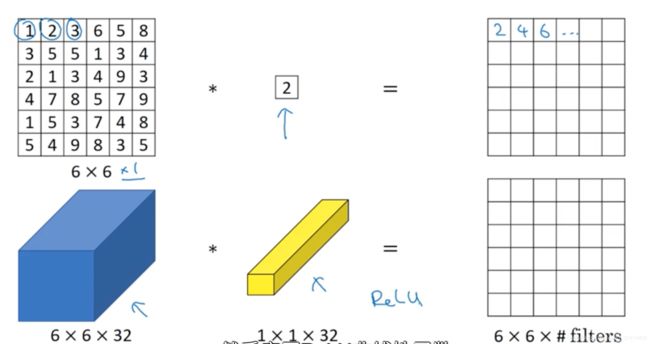
- 下面这个卷积操作,就将一个 6 ∗ 6 ∗ 32 6*6*32 6∗6∗32的输入变成了一个 6 ∗ 6 6*6 6∗6的输入
- 1 ∗ 1 ∗ 32 1*1*32 1∗1∗32这个过滤器中的这32个数字可以理解为:第二层的一个神经元的输入有32个神经元,乘以32个权重之后相加,然后再使用ReLU非线性函数,最终得到第二层的一个数值。
- 如果有多个过滤器,那么最后形成的就不是一个 6 ∗ 6 6*6 6∗6矩阵了,而是 6 ∗ 6 ∗ f i l t e r s 6*6*filters 6∗6∗filters这样一个三维立方体
- 1 ∗ 1 1*1 1∗1卷积核就可以理解为这32个单元都应用了一个全连接神经网络,这个网络输入的是32个神经单元,输出的是filters的个数,然后在这36个单元上重复此过程。输出结果就是 6 ∗ 6 ∗ 过 滤 器 的 数 量 6*6*过滤器的数量 6∗6∗过滤器的数量,一般也将其称为“Network in Network”

- 对于上面的这个例子,池化层通常只能压缩其高度和宽度,但当通道数比较多的时候,使用1*1卷积核,就可以压缩其通道数。
ResNet:转载该专栏
- 残差指的是什么?
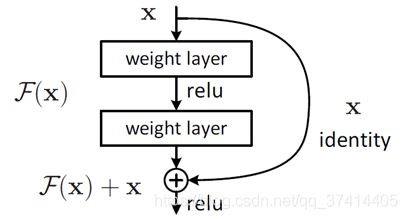
ResNet提出了两种mapping:一种是identity mapping,指的就是图1中”弯弯的曲线”,另一种residual mapping,指的就是除了”弯弯的曲线“那部分,所以最后的输出是 y=F(x)+x
identity mapping顾名思义,就是指本身,也就是公式中的x,而residual mapping指的是“差”,也就是y−x,所以残差指的就是F(x)部分,也就是y-x的差。
- 当残差为0时,此时堆积层仅仅做了恒等映射,至少网络性能不会下降,实际上残差不会为0,这也会使得堆积层在输入特征基础上学习到新的特征,从而拥有更好的性能。残差学习的结构如图所示。这有点类似与电路中的“短路”,所以是一种短路连接(shortcut connection)。
- 为什么ResNet可以解决“随着网络加深,准确率不下降”的问题?
理论上,对于“随着网络加深,准确率下降”的问题,Resnet提供了两种选择方式,也就是identity mapping和residual mapping,如果网络已经到达最优,继续加深网络,residual mapping将被push为0,只剩下identity mapping,这样理论上网络一直处于最优状态了,网络的性能也就不会随着深度增加而降低了。 - ResNet网络是参考了VGG19网络,在其基础上进行了修改,并通过短路机制加入了残差单元,如图5所示。

变化主要体现在ResNet直接使用stride=2的卷积做下采样,并且用global average pool层替换了全连接层。ResNet的一个重要设计原则是:当feature map大小降低一半时,feature map的数量增加一倍,这保持了网络层的复杂度。
图中虚线表示feature map数量发生了改变。从表中可以看到,对于18-layer和34-layer的ResNet,其进行的两层间的残差学习,当网络更深时,其进行的是三层间的残差学习,三层卷积核分别是1x1,3x3和1x1,一个值得注意的是隐含层的feature map数量是比较小的,并且是输出feature map数量的1/4。

(图中3*3,64 指的是卷积核为 3 ∗ 3 3* 3 3∗3 结构,一共有64个卷积核
左边的是BasicBlock 右边的是Bottleneck)
这两种结构分别针对ResNet34(左图)和ResNet50/101/152(右图),一般称整个结构为一个”building block“。其中右图又称为”bottleneck design”,目的一目了然,就是为了降低参数的数目,第一个1x1的卷积把256维channel降到64维,然后在最后通过1x1卷积恢复,整体上用的参数数目:1x1x256x64 + 3x3x64x64 + 1x1x64x256 = 69632,而不使用bottleneck的话就是两个3x3x256的卷积,参数数目: 3x3x256x256x2 = 1179648,差了16.94倍。
- 如果F(x)和x的channel个数不同怎么办,因为F(x)和x是按照channel维度相加的,channel不同怎么相加呢?摘录自这里
- 虚线的的Connection部分(”第一个绿色矩形和第三个绿色矩形“)分别是3x3x64和3x3x128的卷积操作,他们的channel个数不同(64和128),所以采用计算方式:
y = F ( x ) + W x y=F(x)+Wx y=F(x)+Wx
其中W是卷积操作,用来调整x的channel维度的
- 虚线的的Connection部分(”第一个绿色矩形和第三个绿色矩形“)分别是3x3x64和3x3x128的卷积操作,他们的channel个数不同(64和128),所以采用计算方式:
对于ResNet50和ResNet101
- 在上表中,一共提出了5种深度的ResNet,分别是18,34,50,101和152,在表最左侧,我们发现所有的网络都分成5部分,分别是:conv1,conv2_x,conv3_x,conv4_x,conv5_x。
- 拿101-layer那列来讲,首先有个输入7x7x64的卷积,然后经过3 + 4 + 23 + 3 = 33个building block,每个block为3层,所以有33 x 3 = 99层,最后有个fc层(用于分类),所以1 + 99 + 1 = 101层,确实有101层网络;
注:101层网络仅仅指卷积或者全连接层,而激活层或者Pooling层并没有计算在内;
这里我们关注50-layer和101-layer这两列,可以发现,它们唯一的不同在于conv4_x,ResNet50有6个block,而ResNet101有23个block,差了17个block,也就是17 x 3 = 51层。
一些Pytorch基础知识补充
1.Conv3d
class torch.nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
Parameters:
- in_channels(int) – 输入信号的通道
- out_channels(int) – 卷积产生的通道
- kernel_size(int or tuple) - 卷积核的尺寸
- stride(int or tuple, optional) - 卷积步长
- padding(int or tuple, optional) - 输入的每一条边补充0的层数
- dilation(int or tuple, optional) – 卷积核元素之间的间距
- groups(int, optional) – 从输入通道到输出通道的阻塞连接数
- bias(bool, optional) - 如果bias=True,添加偏置
2.nn.Conv2d
nn.Conv2d(self, in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True))
参数:
- in_channel: 输入数据的通道数,例RGB图片通道数为3;
- out_channel: 输出数据的通道数,这个根据模型调整;
- kennel_size: 卷积核大小,可以是int,或tuple;kennel_size=2,意味着卷积大小(2,2), kennel_size=(2,3),意味着卷积大小(2,3)即非正方形卷积
- stride:步长,默认为1,与kennel_size类似,stride=2,意味着步长上下左右扫描皆为2, stride=(2,3),左右扫描步长为2,上下为3;
- padding:零填充
有关ResNet源码解读
下面内容搬运这里 : ResNet详细解读

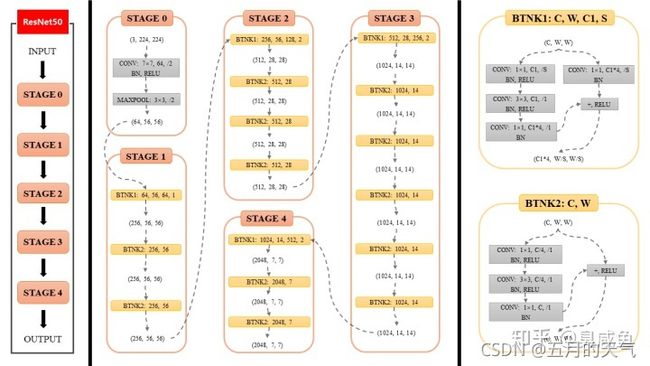
ResNet各个Stage具体结构
如本图所示,ResNet分为5个stage(阶段),其中Stage 0的结构比较简单,可以视其为对INPUT的预处理,后4个Stage都由Bottleneck组成,结构较为相似。Stage 1包含3个Bottleneck,剩下的3个stage分别包括4、6、3个Bottleneck。
现在对Stage 0和Stage 1进行详细描述,同理就可以理解后3个Stage。
Stage 0
(3,224,224)指输入INPUT的通道数(channel)、高(height)和宽(width),即(C,H,W)。现假设输入的高度和宽度相等,所以用(C,W,W)表示。
该stage中第1层包括3个先后操作
CONV
CONV是卷积(Convolution)的缩写,7×7指卷积核大小,64指卷积核的数量(即该卷积层输出的通道数),/2指卷积核的步长为2。
BN
BN是Batch Normalization的缩写,即常说的BN层。
RELU
RELU指ReLU激活函数。
该stage中第2层为MAXPOOL,即最大池化层,其kernel大小为3×3、步长为2。
(64,56,56)是该stage输出的通道数(channel)、高(height)和宽(width),其中64等于该stage第1层卷积层中卷积核的数量,56等于224/2/2(步长为2会使输入尺寸减半)。
总体来讲,在Stage 0中,形状为(3,224,224)的输入先后经过卷积层、BN层、ReLU激活函数、MaxPooling层得到了形状为(64,56,56)的输出。
Stage 1
在理解了Stage 0以及熟悉图中各种符号的含义之后,可以很容易地理解Stage 1。理解了Stage 1之后,剩下的3个stage就不用我讲啦,你自己就能看懂。
Stage 1的输入的形状为(64,56,56),输出的形状为(64,56,56)。
下面介绍Bottleneck的具体结构(难点),把Bottleneck搞懂后,你就懂Stage 1了。
Bottleneck具体结构
现在让我们把目光放在本图最右侧,最右侧介绍了2种Bottleneck的结构。
“BTNK”是BottleNeck的缩写(本文自创,请谨慎使用)。
2种Bottleneck分别对应了2种情况:输入与输出通道数相同(BTNK2)、输入与输出通道数不同(BTNK1),这一点可以结合ResNet原文去看喔。
BTNK2
我们首先来讲BTNK2。
BTNK2有2个可变的参数C和W,即输入的形状(C,W,W)中的c和W。
令形状为(C,W,W)的输入为[公式],令BTNK2左侧的3个卷积块(以及相关BN和RELU)为函数[公式],两者相加([公式])后再经过1个ReLU激活函数,就得到了BTNK2的输出,该输出的形状仍为(C,W,W),即上文所说的BTNK2对应输入[公式]与输出[公式]通道数相同的情况。
BTNK1
BTNK1有4个可变的参数C、W、C1和S。
与BTNK2相比,BTNK1多了1个右侧的卷积层,令其为函数[公式]。BTNK1对应了输入[公式]与输出[公式]通道数不同的情况,也正是这个添加的卷积层将[公式]变为[公式],起到匹配输入与输出维度差异的作用([公式]和[公式]通道数相同),进而可以进行求和[公式]。
简要分析
可知,ResNet后4个stage中都有BTNK1和BTNK2。
4个stage中BTNK2参数规律相同
4个stage中BTNK2的参数全都是1个模式和规律,只是输入的形状(C,W,W)不同。
Stage 1中BTNK1参数的规律与后3个stage不同
然而,4个stage中BTNK1的参数的模式并非全都一样。具体来讲,后3个stage中BTNK1的参数模式一致,Stage 1中BTNK1的模式与后3个stage的不一样,这表现在以下2个方面:
参数S:BTNK1左右两个1×1卷积层是否下采样
Stage 1中的BTNK1:步长S为1,没有进行下采样,输入尺寸和输出尺寸相等。
后3个stage的BTNK1:步长S为2,进行了下采样,输入尺寸是输出尺寸的2倍。
参数C和C1:BTNK1左侧第一个1×1卷积层是否减少通道数
Stage 1中的BTNK1:输入通道数C和左侧1×1卷积层通道数C1相等(C=C1=64),即左侧1×1卷积层没有减少通道数。
后3个stage的BTNK1:输入通道数C和左侧1×1卷积层通道数C1不相等(C=2*C1),左侧1×1卷积层有减少通道数。
为什么Stage 1中BTNK1参数的规律与后3个stage不同?(个人观点)
关于BTNK1左右两个1×1卷积层是否下采样
因为Stage 0中刚刚对网络输入进行了卷积和最大池化,还没有进行残差学习,此时直接下采样会损失大量信息;而后3个stage直接进行下采样时,前面的网络已经进行过残差学习了,所以可以直接进行下采样。
关于BTNK1左侧第一个1×1卷积层是否减少通道数
根据ResNet原文可知,Bottleneck左侧两个1×1卷积层的主要作用分别是减少通道数和恢复通道数,这样就可以使它们中间的3×3卷积层的输入和输出的通道数都较小,因此效率更高。
Stage 1中BTNK1的输入通道数C为64,它本来就比较小,因此没有必要通过左侧第一个1×1卷积层减少通道数。
ResNet-50的Pytorch实现:
import torch.nn as nn
def conv1x1(in_channels, out_channels, stride=1):
return nn.conv2d(in_channels, out_channels, kernel_size = 1, stride = stride, bias=False)
def conv3x3(in_channels, out_channels, kernel_size, stride=1):
return nn.conv2d(in_channels, out_channels, kernel_size=3, stride=stride, bias=False)
def conv7x7(in_channels, out_channels, stride, padding=3):
return nn.conv2d(in_channels, out_channels, kernel_size=7, stride=stride, padding=padding, bias=False)
class Bottleneck(nn.module):
expansion = 4
def __init__(self, in_channels, out_channels, stride=1, downsample=None):
super(Bottleneck, self).__init__()
self.conv1 = conv1x1(in_channels, out_channels) #这里为什么不传入stride stage1中的stride=1,不需要下采样 因为刚经过一个maxpooling
self.bn1 = nn.BatchNorm2d(out_channels)
self.conv2 = conv3x3(out_channels, out_channels, stride)
self.bn2 = nn.BatchNorm2d(out_channels)
#为什么这么设计
self.conv3 = conv1x1(out_channels, out_channels * self.expansion)
self.bn3 = nn.BatchNorm2d(out_channels * self.expansion)
self.relu = nn.ReLU(inplace=True)
self.downsample = downsample
self.stride = stride
def forward(self, x):
residual = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
#stage1 的输入输出通道不同的不需要下采样
if self.downsample is not None:
residual = self.downsample(x) #使用卷积将输入的通道数转换成和输出通道数目一样
out += residual
out = self.relu(out)
return out
class ResNet_50(nn.module):
def __init__(self, layers, num_classes=1000 ):
super(ResNet_50,self).__init__()
#这一步自己忘记加
self.in_channels = 64
self.conv1 = conv7x7(3,64)
self.bn1 = nn.BatchNorm2d(64) #num_features – C from an expected input of size (N, C, H, W)(N,C,H,W) 通道数
self.relu = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
self.layer1 = self._make_layer(64, layers[0]) #layers代表有几层 这里的64代表1x1卷积层的输出
self.layer2 = self._make_layer(128, layers[1], stride = 2)
self.layer3 = self._make_layer(256, layers[2], stride = 2)
self.layer4 = self._make_layer(512, layers[3], stride = 2)
self.avgpool = nn.AdaptiveAvgPool2d(7)
self.fc = nn.Linear(512 * Bottleneck.expansion, num_classes)
#fc层
def _make_layer(self, out_channels, layer_num, stride=1):
downsample = None
if stride != 1 or self.in_channels != out_channels * Bottleneck.expansion:
downsample = nn.Sequential(
conv1x1(self.in_channels, out_channels * Bottleneck.expansion, stride),
nn.BatchNorm2d(out_channels * Bottleneck.expansion)
)
layers = []
layers.append(Bottleneck(self.in_channels, out_channels, stride, downsample ) )
self.in_channels = out_channels * Bottleneck.expansion #这里只变输入是因为卷积的输出都是固定的
for _ in range(1, layer_num):
layers.append( Bottleneck(self.in_channels, out_channels) )
return nn.Sequential(*layers)
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu(x)
x = self.maxpool(x)
x = self.layer1(x)
x = self.layer2(x)
x = self.layer3(x)
x = self.layer4(x)
x = self.avgpool(x)
x = self.fc(x)
return x
