深度学习基础之代价函数
文章目录
- 一、代价函数概述
- 二、代价函数的原理
- 三、常见的代价函数
-
- 1. 二次代价函数(quadratic cost)
- 2. 交叉熵代价函数(cross-entropy)
- 3. 对数似然代价函数(log-likelihood cost)
- 四、二次代价函数与交叉熵代价函数比较
在机器学习和深度学习中,经常听到代价函数这个词,到底什么是代价函数?
一、代价函数概述
机器学习的模型分为能量模型和概率模型,知道概率分布的可以直接用概率模型进行建模,比如贝叶斯分类器,不知道的就用能量模型,比如支持向量机。因为一个系统稳定的过程就是能量逐渐减小的过程。
简单理解,代价函数也就是通常建立的能量方程的一种,在机器学习中用来衡量预测值和真实值之间的误差,越小越好。一般来说一个函数有解析解和数值解,解析解就是我们数学上可以用公式算出来的解,数值解是一种近似解,在解析解不存在或者工程实现比较复杂的时候,用例如梯度下降这些方法,迭代得到一个效果还可以接受的解。所以要求代价函数对参数可微。
代价函数、损失函数、目标函数并不一样,这一点后边再介绍,这篇文章就先只介绍代价函数。
损失函数:计算的是一个样本的误差
代价函数:是整个训练集上所有样本误差的平均
目标函数:代价函数 + 正则化项
在实际中,损失函数和代价函数是同一个东西,目标函数是一个与他们相关但更广的概念。
代价函数(Cost Function):在机器学习中,代价函数作用于整个训练集,是整个样本集的平均误差,对所有损失函数值的平均。
代价函数的作用:
- 1.为了得到训练逻辑回归模型的参数,需要一个代价函数,通过训练代价函数来得到参数。
- 2.用于找到最优解的目标函数。
二、代价函数的原理
在回归问题中,通过代价函数来求解最优解,常用的是平方误差代价函数。有如下假设函数:
h ( x ) = A + B x h(x)=A+Bx h(x)=A+Bx
假设函数中有A和B两个参数,当参数发生变化时,假设函数状态也会随着变化。 如下图所示
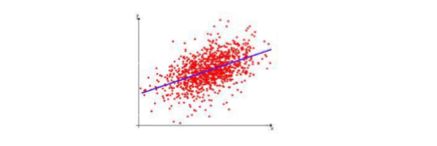
想要拟合图中的离散点,我们需要尽可能找到最优的 A A A和 B B B来使这条直线更能代表所有数据。如何找到最优解呢,这就需要使用代价函数来求解,以平方误差代价函数为例,假设函数为 h ( x ) = θ 0 x h(x)=\theta_0x h(x)=θ0x 。
平方误差代价函数的主要思想就是将实际数据给出的值与拟合出的线的对应值做差,求出拟合出的直线与实际的差距。在实际应用中,为了避免因个别极端数据产生的影响,采用类似方差再取二分之一的方式来减小个别数据的影响。因此,引出代价函数:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 J(\theta _0,\theta _1)=\frac{1}{2m}\sum_{i=1}^{m}(h(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1i=1∑m(h(x(i))−y(i))2
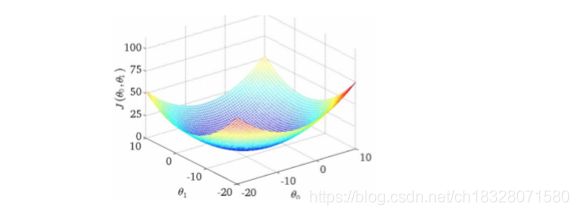
最优解即为代价函数的最小值 m i n J ( θ 0 , θ 1 ) minJ(\theta _0,\theta _1) minJ(θ0,θ1)。如果是 1 个参数,代价函数一般通过二维曲线便可直观看出。如果是 2 个参数,代价函数通过三维图像可看出效果,参数越多,越复杂。
当参数为 2 个时,代价函数是三维图像。
- 1.非负性,所以目标就是最小化代价函数。
- 2.当真实输出 a a a与期望输出 y y y接近的时候,代价函数接近于0。(比如 y = 0 y=0 y=0, a ~ 0 a~0 a~0; y = 1 y=1 y=1,a~1时,代价函数都接近0)。
代价函数非负的原因:
- 目标函数存在一个下界,在优化过程当中,如果优化算法能够使目标函数不断减小,根据单调有界准则,这个优化算法就能证明是收敛有效的。
- 只要设计的目标函数有下界,基本上都可以,代价函数非负更为方便。
三、常见的代价函数
1. 二次代价函数(quadratic cost)
J = 1 2 n ∑ i = 1 ∣ ∣ y ( x ) − a L ( x ) ∣ ∣ 2 J=\frac{1}{2n}\sum_{i=1}\left | \right |y(x)-a^{L}(x)\left | \right |^2 J=2n1i=1∑∣∣y(x)−aL(x)∣∣2
其中, J J J 表示代价函数, x x x表示样本, y y y表示实际值, a a a表示输出值, n n n表示样本的总数。 使用一个样本为例简单说明,此时二次代价函数为:
J = ( y − a ) 2 2 J=\frac{(y-a)^2}{2} J=2(y−a)2
假如使用梯度下降法来调整权值参数的大小,权值 w w w和偏置 b b b的梯度推 导如下:
∂ J ∂ w = ( a − y ) δ ′ ( z ) x \frac{\partial J}{\partial w}=(a-y){\delta }'(z)x ∂w∂J=(a−y)δ′(z)x
∂ J ∂ b = ( a − y ) δ ′ ( z ) \frac{\partial J}{\partial b}=(a-y){\delta }'(z) ∂b∂J=(a−y)δ′(z)
其中, z z z表示神经元的输入, δ \delta δ 表示激活函数。权值 w w w和偏置 b b b的梯度跟激活函数的梯度成正比,激活函数的梯度越大,权值 w w w和偏置 b b b的大小调整得越快,训练收敛得就越快。
2. 交叉熵代价函数(cross-entropy)
交叉熵代价函数:
J = − 1 n ∑ i = 1 [ y l n a + ( 1 − y ) l n ( 1 − a ) ] J=-\frac{1}{n}\sum_{i=1}[ ylna+(1-y)ln(1-a)] J=−n1i=1∑[ylna+(1−y)ln(1−a)]
其中, J J J 表示代价函数, x x x表示样本, y y y 表示实际值, a a a表示输出值, n n n表示样本的总数。 权值 w w w和偏置 b b b的梯度推导如下:
∂ J ∂ w j = 1 n ∑ x x j ( δ ( x ) − y ) \frac{\partial J}{\partial w_j}=\frac{1}{n}\sum_{x}x_j(\delta(x)-y) ∂wj∂J=n1x∑xj(δ(x)−y)
∂ J ∂ b = 1 n ∑ x ( δ ( x ) − y ) \frac{\partial J}{\partial b}=\frac{1}{n}\sum_{x}(\delta(x)-y) ∂b∂J=n1x∑(δ(x)−y)
当误差越大时,梯度就越大,权值 w w w和偏置 b b b调整就越快,训练的速度也就越快。 二次代价函数适合输出神经元是线性的情况,交叉熵代价函数适合输出神经元是 S S S 型函 数的情况。
3. 对数似然代价函数(log-likelihood cost)
对数释然函数常用来作为 softmax 回归的代价函数。深度学习中普遍的做法是将 softmax 作为最后一层,此时常用的代价函数是对数释然代价函数。
Softmax回归中将x分类为类别j的概率为:
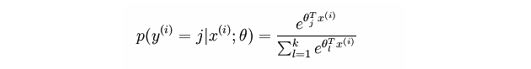
或者:
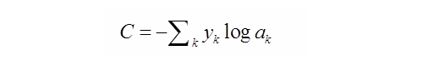
对数似然代价函数与 softmax 的组合和交叉熵与 sigmoid 函数的组合非常相似。对数释然 代价函数在二分类时可以化简为交叉熵代价函数的形式:
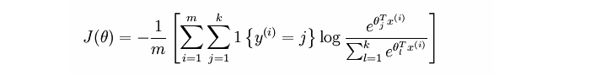
其中, y k y_k yk表示第 k k k个神经元的输出值, a k a_k ak表示第 k k k个神经元对应的真实值,取值为 0 0 0或 1 1 1。
简单理解一下这个代价函数的含义:在网络中输入一个样本,那么只有一个神经元对应了该样本的正确类别;若这个神经元输出的概率值越高,则按照以上的代价函数公式,其产生的代价就越小;反之,则产生的代价就越高。
四、二次代价函数与交叉熵代价函数比较
1.当我们用sigmoid函数作为神经元的激活函数时,最好使用交叉熵代价函数来替代方差代价函数。
- 因为使用二次代价函数时,偏导数受激活函数的导数影响,sigmoid 函数导数在输出接近 0 和 1 时非常小,会导致一 些实例在刚开始训练时学习得非常慢。而使用交叉熵代价函数时,,权重学习的速度受到 ( δ ( z ) − y ) (\delta(z)-y) (δ(z)−y)的影响,更大的误差,就有更快的学习速度,避免了二次代价函数方程中因 δ ′ ( z ) {\delta }'(z) δ′(z)
导致的学习缓慢的情况。
2.交叉熵函数的形式是 − [ y l n a + ( 1 − y ) l n ( 1 − a ) ] −[ylna+(1−y)ln(1−a)] −[ylna+(1−y)ln(1−a)]。而不是 − [ a l n y + ( 1 − a ) l n ( 1 − y ) ] −[alny+(1−a)ln(1−y)] −[alny+(1−a)ln(1−y)]。
是因为当期望输出的 y = 0 y=0 y=0时, l n y lny lny没有意义;当期望 y = 1 y=1 y=1时, l n ( 1 − y ) ln(1-y) ln(1−y)没有意义。而因为a是sigmoid函数的实际输出,永远不会等于0或1,只会无限接近于0或者1,因此不存在这个问题。