LRU 不知道?这个生活实例一定知道吧!
Hello,好久不见。
由于各种原因断更了挺久的,在这给等待我更新的小伙伴们说声抱歉!
接下来的日子,让我们调整步伐继续向前!今天是 Kevin 的算法之路的第 73 天。和大家分享著名常考的 LRU 算法以及解决 LeetCode 的第 146 题。
LRU 算法思想
LRU,全称是 Least Recently Used,即最近最少使用。是一种缓存淘汰策略算法。
这个算法的思想就是:如果一个数据在最近一段时间没有被访问到,那么在将来它被访问的可能性也很小。所以,当指定的空间已存满数据时,应当把最久没有被访问到的数据淘汰。
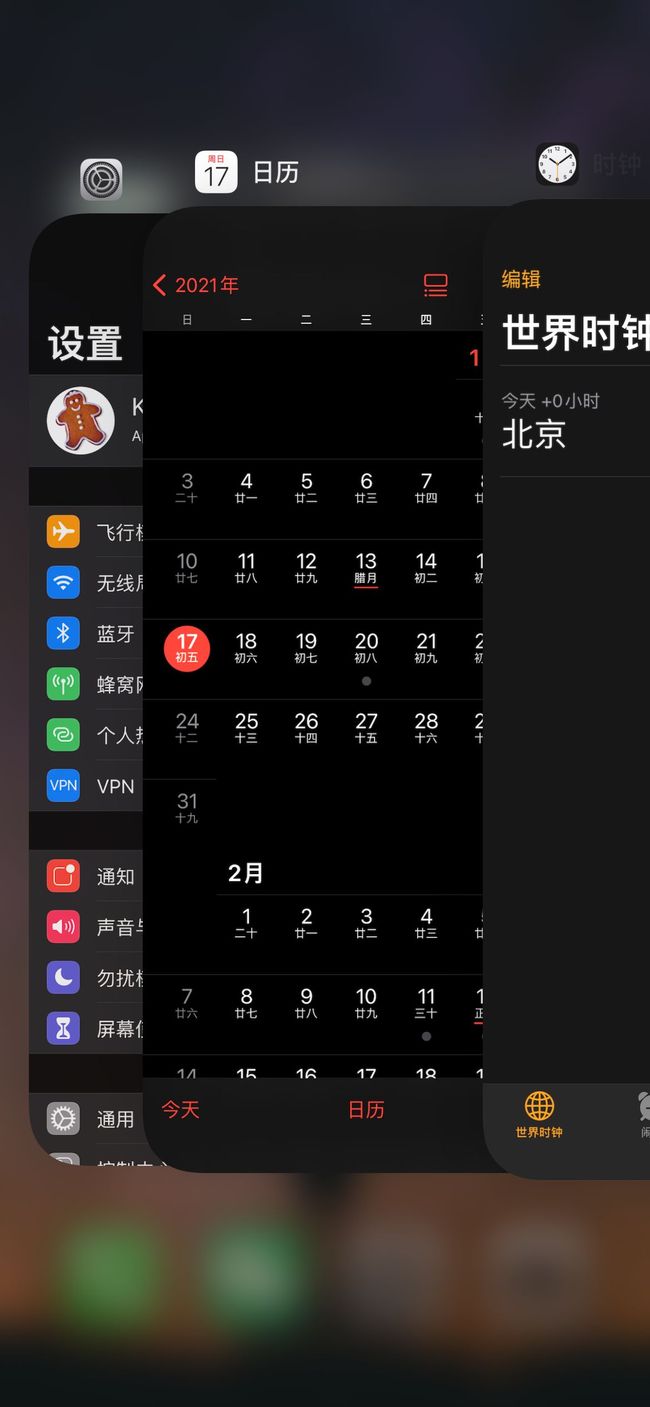
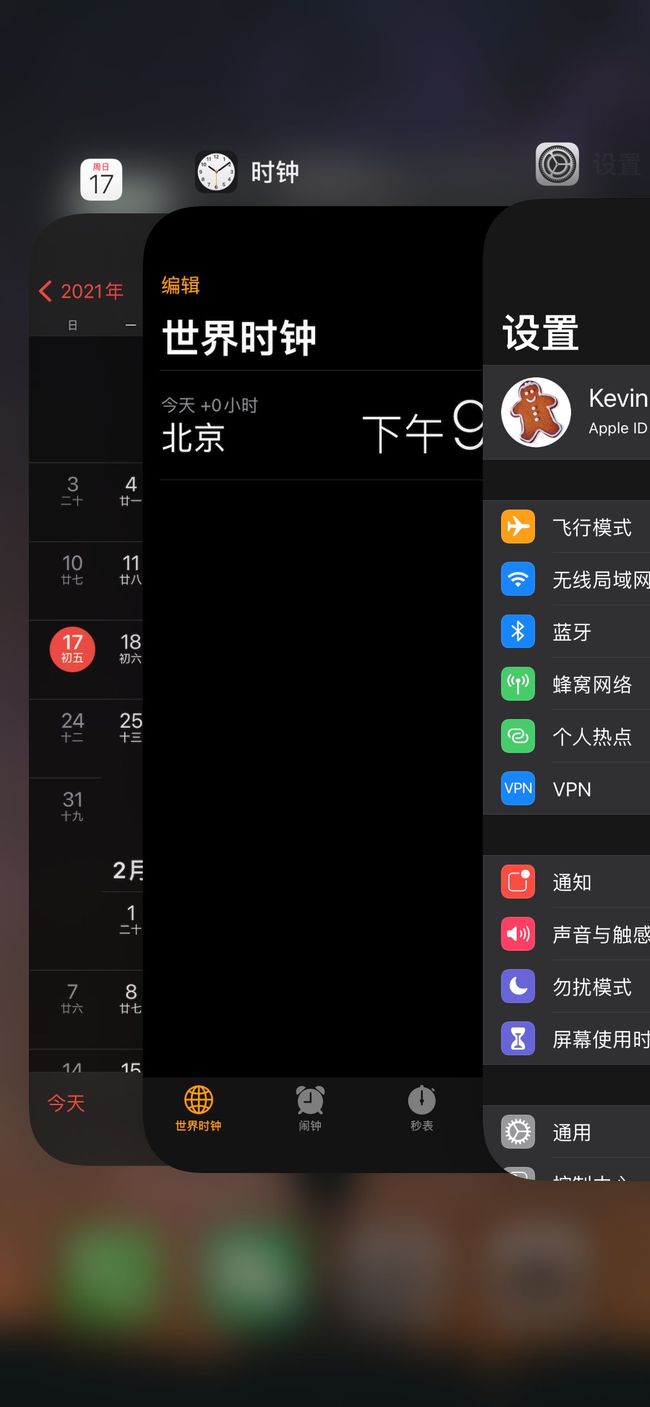
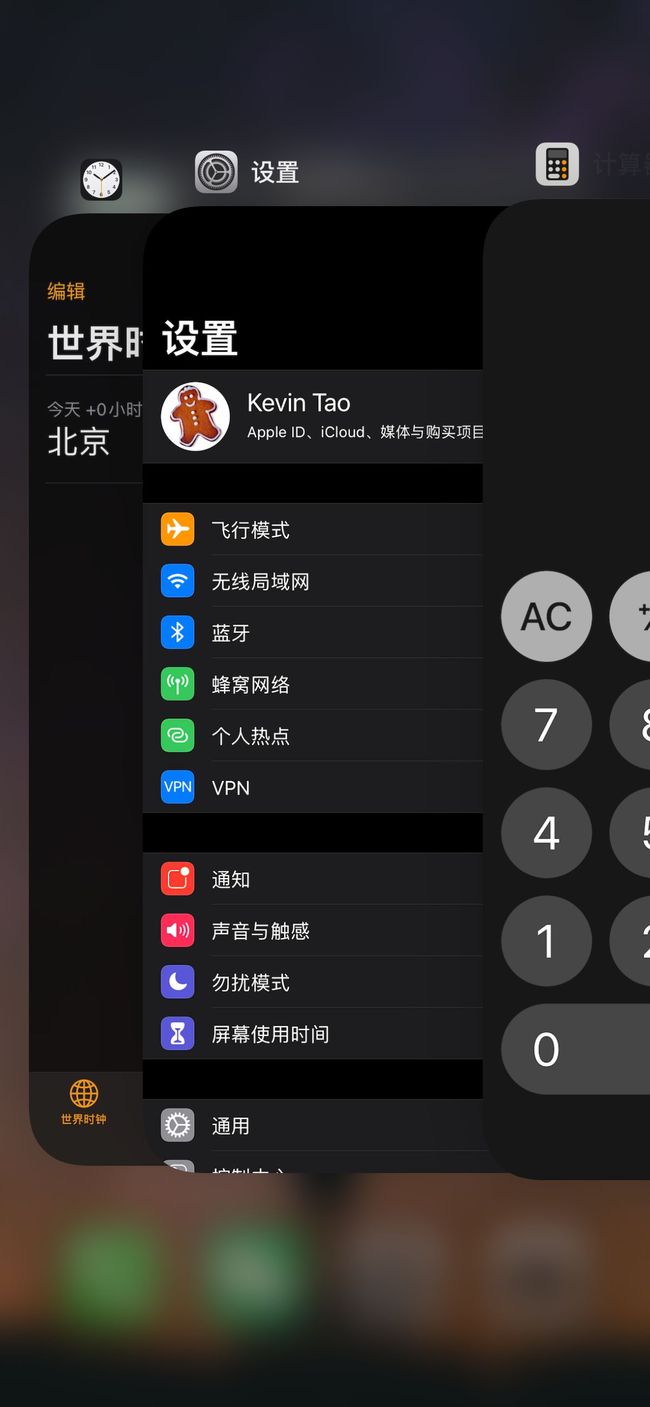
举个简单的例子,现在的智能手机都可以把应用程序放在后台运行,比如我先后打开了「设置」「日历」「时钟」,那么它们在后台的排序是这样的:
如果这时我访问了「设置」,那么「设置」就会被放置到第一个,变成这样:
假如我的手机最多只允许我同时开 3 个应用,现在已经满了。那么如果我想新开一个应用「计算器」,就必须关闭一个应用以腾出空间,那么关闭哪一个呢?
按照 LRU 算法,就关闭最底下的「日历」,因为那是最近最少使用的,然后把新的应用放置到最上面。
现在你应该理解了 LRU 算法思想了,那么我们接下来考虑如何实现。
LRU 算法描述
力扣第 146 题「LRU缓存机制」就是让我们设计实现 LRUCache 类:
-
LRUCache(int capacity)以正整数作为容量capacity初始化 LRU 缓存 -
int get(int key)如果关键字 key 存在于缓存中,则返回关键字的值,否则返回-1。 -
void put(int key, int value)如果关键字已经存在,则变更其数据值;如果关键字不存在,则插入该组「关键字-值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
进阶要求我们是否可以在 O(1) 时间复杂度内完成 get 和 put 两种操作?
我们举个例子看看 LRU 算法是如何工作的:
/* 缓存容量为 2 */
LRUCache cache = new LRUCache(2);
// 你可以把 cache 理解成一个队列
// 假设左边是队头,右边是队尾
// 最近使用的排在队头,久未使用的排在队尾
// 圆括号表示键值对 (key, val)
cache.put(1, 1);
// cache = [(1, 1)]
cache.put(2, 2);
// cache = [(2, 2), (1, 1)]
cache.get(1); // 返回 1
// cache = [(1, 1), (2, 2)]
// 解释:因为最近访问了键 1,所以提前至队头
// 返回键 1 对应的值 1
cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// 解释:缓存容量已满,需要删除内容空出位置
// 优先删除久未使用的数据,也就是队尾的数据
// 然后把新的数据插入队头
cache.get(2); // 返回 -1 (未找到)
// cache = [(3, 3), (1, 1)]
// 解释:cache 中不存在键为 2 的数据
cache.put(1, 4);
// cache = [(1, 4), (3, 3)]
// 解释:键 1 已存在,把原始值 1 覆盖为 4
// 不要忘了也要将键值对提前到队头
LRU 算法设计
方法一:数组
用一个数组来存储数据,我们可以给每个数据项做标记值来实现 LRU 算法。
每次访问数组中的数据项的时候,将被访问的数据项的标记值置为0。
每次插入新数据项的时候,先把数组中存在的数据项的标记值自增,并将新数据项的标记值置为 0 并插入到数组中。
当数组空间已满时,将标记值最大的数据项淘汰。
这种方法比较好理解,但也有明显的缺点:需要不停地维护数组中元素的标记值。
每次操作都伴随着一次遍历数组修改标记的操作,所以时间复杂度是 O(n)。
方法二:单链表
用一个有序单链表,我们可以通过控制链表的顺序实现 LRU 算法。
假设我们将新元素插入到链表的尾部(当然也可以插入到链表的头部),所以越靠近链表头部的结点是越早之前访问的。
每次访问链表中的元素时,将其从原来的位置删除,并插入到链表尾部。
每次插入新元素的时候,直接在链表尾部插入新元素。
当链表已满时,先删除链表头部的元素,再在链表尾部插入新元素。
这种方法感觉比数组高级一点,但由于需要访问链表,其时间复杂度还是 O(n)。
方法三:哈希表+双向链表
如果我们想要查询和插入的时间复杂度都是 O(1),那么我们需要一个满足下面三个条件的数据结构:
- 这个数据结构必须是有序的,以区分最近使用的和很久没有使用的数据,当容量满了之后,要删除最久未使用的那个元素。
- 要在这个数据结构中快速找到某个 key 是否存在,并返回其对应的 value。
- 每次访问这个数据结构中的某个 key,需要将这个元素变为最近使用的。也就是说,这个数据结构要支持在任意位置快速插入和删除元素。
那么,什么样的数据结构同时符合上面的条件呢?
查找快,我们能想到哈希表。但是哈希表的数据是乱序的。
有序,我们能想到链表,插入、删除都很快,但是查询慢。
所以,我们得让哈希表和链表结合一下,形成一个新的数据结构,那就是:哈希链表,LinkedHashMap。
LRU 缓存算法的核心数据结构就是哈希链表,这个数据结构长这样:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-73Vlvvnp-1610948870515)(http://goleetcode.ifree258.top/014604.jpg)]
借助这个数据结构,我们来一一分析以上三个条件:
- 如果我们每次默认从链表尾部添加元素,那么越靠近链表头部的就是最久未使用的元素。
- 对于某一个
key,我们可以通过哈希表快速定位到链表中的节点,从而取得对应val。- 链表显然是支持在任意位置快速插入和删除的,改改指针就行。只不过传统的链表无法按照索引快速访问某一个位置的元素,而这里借助哈希表,可以通过
key快速映射到任意一个链表节点,然后进行插入和删除。
也许你会问,为什么要是双向链表,单链表行不行?另外,既然哈希表中已经存了 key,为什么链表中还要存 key 和 val 呢,只存val 不行吗?
我们通过代码来解答这两个问题。
LRU 代码实现
很多编程语言都有内置的哈希链表或者类似 LRU 功能的库函数,比如 Java 中的 LinkedHashMap 。但是为了帮大家理解算法的细节,我们先自己造轮子实现一遍 LRU 算法。以下使用 Go 语言实现,理解了思想相信你用其他语言一样可以实现。
首先,我们定义双链表的节点类:
// 链表节点
type Node struct {
key, val int // 键、值
prev, next *Node // 前、后
}
func initNode(key, val int) *Node {
return &Node{
key: key,
val: val,
}
}
然后,借助节点实现双向链表,以及几个 LRU 算法需要用到的 API:
// 双向链表
type DoubleLinkedList struct {
head, tail *Node // 虚拟头节点、虚拟尾节点
size int // 链表元素数
}
func initDoubleLinkedList() *DoubleLinkedList {
dll := &DoubleLinkedList{
head: initNode(0, 0),
tail: initNode(0, 0),
size: 0,
}
dll.head.next = dll.tail
dll.tail.prev = dll.head
return dll
}
// 在链表尾部添加 x 节点,时间 O(1)
func (this *DoubleLinkedList) addLast(x *Node) {
x.prev = this.tail.prev
x.next = this.tail
// 注意!上面两行和下面两行不能颠倒
this.tail.prev.next = x
this.tail.prev = x
this.size++
}
// 删除链表中的 x 节点,时间 O(1)
func (this *DoubleLinkedList) remove(x *Node) {
x.prev.next = x.next
x.next.prev = x.prev
x.prev = nil
x.next = nil
this.size--
}
// 删除链表中的第一个节点,并返回该节点,时间 O(1)
func (this *DoubleLinkedList) removeFirst() *Node {
if this.head.next == this.tail {
return nil
}
first := this.head.next
this.remove(first)
return first
}
这里就可以回答前面提出的「为什么必须要用双向链表」的问题了,因为我们需要删除操作。删除一个节点不光要得到该节点本身的指针,也需要操作其前驱节点的指针,而双向链表才能支持直接查找前驱,保证操作的时间复杂度 O(1)。
注意我们实现的双链表 API 只能从尾部插入,也就是说靠尾部的数据是最近使用的,靠头部的数据是最久为使用的。
有了双向链表,我们可以将其与哈希表结合实现 LRU:
type LRUCache struct {
capacity int // 容量
knMap map[int]*Node // key -> Node(key, val)
cache *DoubleLinkedList // Node(k1, v1) <-> Node(k2, v2)...
}
func Constructor(capacity int) LRUCache {
lruCache := LRUCache{
capacity: capacity,
knMap: map[int]*Node{},
cache: initDoubleLinkedList(),
}
return lruCache
}
我们先不着急去实现 LRU 算法的 get 和 put 方法。我们要同时维护一个双链表 cache 和一个哈希表 knMap,很容易漏掉一些操作,比如说删除某个 key 时,在 cache 中删除了对应的 Node,但是却忘记在 knMap 中删除 key。
解决这种问题的有效方法是:封装一层 API 对两种数据结构进行操作。尽量让 LRU 的主方法 get 和 put 避免直接操作 map 和 cache 的细节。我们可以先实现下面几个函数:
// 将某个 key 调整为最近使用的元素
func (this *LRUCache) makeRecently(key int) {
// 找到节点
node := this.knMap[key]
// 删除节点
this.cache.remove(node)
// 添加到链表尾部
this.cache.addLast(node)
}
// 添加最近使用的元素
func (this *LRUCache) addRecently(key int, val int) {
// 初始化节点
node := initNode(key, val)
// 添加到链表尾
this.cache.addLast(node)
// 别忘了关联map映射
this.knMap[key] = node
}
// 删除某一个 key 及对应元素
func (this *LRUCache) deleteKey(key int) {
node := this.knMap[key]
// 删除节点
this.cache.remove(node)
// 删除映射
delete(this.knMap, key)
}
// 删除最近最少使用的元素
func (this *LRUCache) deleteLRU() {
// 链表的第一个就是最近最少使用的元素
deletedNode := this.cache.removeFirst()
// 删除映射
delete(this.knMap, deletedNode.key)
}
这里就能回答之前的问答题「为什么要在链表中同时存储 key 和 val,而不是只存储 val」,注意 deleteLRU 函数中,我们需要用 deletedNode 得到 deletedNode.key。
也就是说,当缓存容量已满,我们不仅仅要删除最后一个 Node 节点,还要把 map 中映射到该节点的 key 同时删除,而这个 key 只能由 Node 得到。如果 Node 结构中只存储 val,那么我们就无法得知 key 是什么,就无法删除 map 中的键,造成错误。
上述方法就是简单的操作封装,调用这些函数可以避免直接操作 cache 链表和 map 哈希表,下面我先来实现 LRU 算法的 get 方法:
func (this *LRUCache) Get(key int) int {
node, exist := this.knMap[key]
if !exist {
// 未找到,返回 -1
return -1
}
// 找到,将其设为最近使用
this.makeRecently(key)
return node.val
}
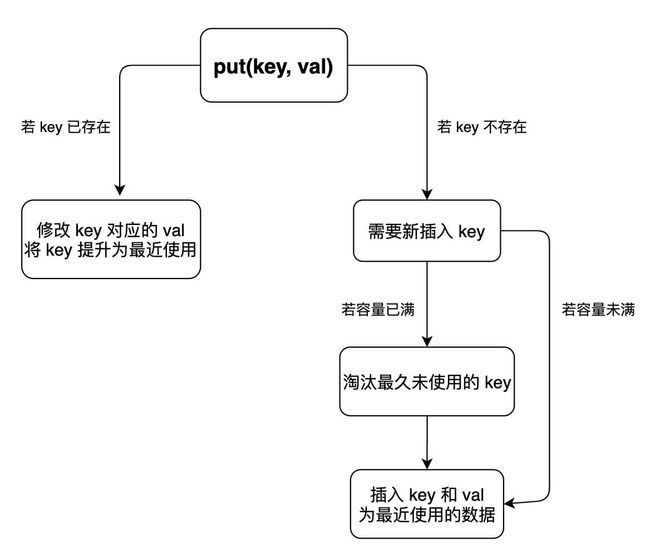
put 方法稍微复杂一些,我们先来画个图搞清楚它的逻辑:
我们可以清晰的写出put 方法的代码:
func (this *LRUCache) Put(key int, value int) {
_, exist := this.knMap[key]
// 如果存在
if exist {
// 删除旧元素
this.deleteKey(key)
// 添加新数据为最近使用
this.addRecently(key, value)
} else {
// 不存在
// 容量满
if this.cache.size == this.capacity {
// 删除最近最少使用的元素
this.deleteLRU()
}
// 添加元素为最近使用
this.addRecently(key, value)
}
}
以上。我们就完成了 LRU 算法。
郑重声明:
所展示代码已通过 LeetCode 运行通过,请放心食用~
参考:
https://labuladong.gitbook.io/
https://mp.weixin.qq.com/s/F5z4_CWmvc_s3Aly3eb6aQ
在唠唠嗑
很多人都想养成好习惯,但大多数人却是三分钟热度。为了我们能一起坚持下去,决定制定如下计划(福利)
一起学算法,打卡领红包!
参与方式:
关注我的微信公众号「Kevin的学堂」
还可「加群」与众多小伙伴
一起坚持,一起学习,一起更优秀!
打卡规则为:
「留言」“打卡XXX天” ➕「分享」到朋友圈
奖励:
打卡
21天,联系本人获取6.6元红包一个!打卡
52天,联系本人获取16.6元红包一个!打卡
100天,联系本人获取66.6元红包一个!
读者福利
最近有读者反馈有些算法题比较难懂,据沟通发现是缺乏一些基础知识,所以我将自己现有的资源整理出来分享给大家,其中包括【数据结构和算法、计算机基础、Java、Python、Golang等学习视频和电子书,以及面试和项目资源】希望能帮助到大家~
获取方法:关注我的公众号【Kevin的学堂】回复【资源】即可免费获取!
最后,感谢你能看到这里!
坚持原创不易,如果你觉得还不错的话,求【点赞】【在看】【转发】三连安排,你的支持就是我最大的动力!
推荐阅读
一日一力扣|第64天:颜色分类
leetcode|一道算法题错失谷歌offer
leetcode|智慧树下你和我