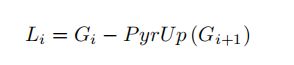OpenCv-Python学习笔记(十一)：图像金字塔

目录

demo

高斯金字塔

1、cv.pyrDown()函数

2、cv2.pyrUp()函数

拉普拉斯金字塔

---

图像金字塔：创建一组图像，这些图像是具有不同分辨率的原始图像，简单来说就是同一图像的不同分辨率的子图集合，把最大的图像放在底部，最小的放在顶部，像是金字塔。

demo

第一步：读入两幅图像，苹果和橘子

第二步：构建苹果和橘子的高斯金字塔（5层）

第三步：根据高斯金字塔计算拉普拉斯金字塔

第四步：在拉普拉斯的每一层进行图像融合（苹果的左边和橘子的右边进行融合）

第五步：根据融合后的图像金字塔构建原始图像。

import cv2
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
import numpy as np
apple = cv2.imread("./apple.png")
orange = cv2.imread("./orange.png")
apple = cv2.resize(apple,(288,288)) #将图片大小扩展到(288,288),这里为什么需要将图片扩张到(288,288)在文章最后会解释
orange = cv2.resize(orange,(288,288))

#构建苹果的高斯金字塔
#apple_GaussPys = [原图，下采样1次，下采样2次，下采样3次，下采样4次，下采样5次]
apple_GaussDown = apple
apple_GaussDowns = [apple]
for i in range(4):
    apple_GaussDown = cv2.pyrDown(apple_GaussDown)
    apple_GaussDowns.append(apple_GaussDown)

#构建橘子的高斯金字塔
#orange_GaussPys = [原图，下采样1次，下采样2次，下采样3次，下采样4次，下采样5次]
orange_GaussDown = orange
orange_GaussDowns = [orange]
for i in range(4):
    orange_GaussDown = cv2.pyrDown(orange_GaussDown)
    orange_GaussDowns.append(orange_GaussDown)

#构建苹果的拉普拉斯金字塔
#i一次取值5,4,3,2,1
apple_Laplaces = [apple_GaussDowns[4]]
for i in range(4,0,-1):
    apple_GaussUp = cv2.pyrUp(apple_GaussDowns[i])
    apple_Laplace = cv2.subtract(apple_GaussDowns[i-1],apple_GaussUp)
    apple_Laplaces.append(apple_Laplace)

#构建橘子的拉普拉斯金字塔
orange_Laplaces = [orange_GaussDowns[4]]
for i in range(4,0,-1):
    rows, cols, channel = orange_GaussDowns[i - 1].shape
    orange_GaussUp = cv2.pyrUp(orange_GaussDowns[i])
    orange_Laplace = cv2.subtract(orange_GaussDowns[i-1],cv2.resize(orange_GaussUp,(rows,cols)))
    orange_Laplaces.append(orange_Laplace)

#将苹果和橘子的坐标和右边拼接起来
splicing_Laplaces = []
for apple_Laplace,orange_Laplace in zip(apple_Laplaces,orange_Laplaces):
    rows,cols,channel = apple_Laplace.shape
    #hstack将连个数据水平堆叠，形成一个新的array
    splicing_Laplace = np.hstack((apple_Laplace[:,0:int(cols/2)],orange_Laplace[:,int(cols/2):]))
    splicing_Laplaces.append(splicing_Laplace)
#重建
ls_ = splicing_Laplaces[0]
for i in range(1,5):
    ls_ = cv2.pyrUp(ls_)
    ls_ = cv2.add(ls_, splicing_Laplaces[i])

#直接连接图像的一半
rows,cols,channel = apple.shape
real = np.hstack((apple[:,:int(cols/2)],orange[:,int(cols/2):]))

cv2.imshow("apple",apple)
cv2.imshow("orange",orange)
cv2.imshow("laplaces",ls_)
cv2.imshow("real",real)
cv2.waitKey()

 

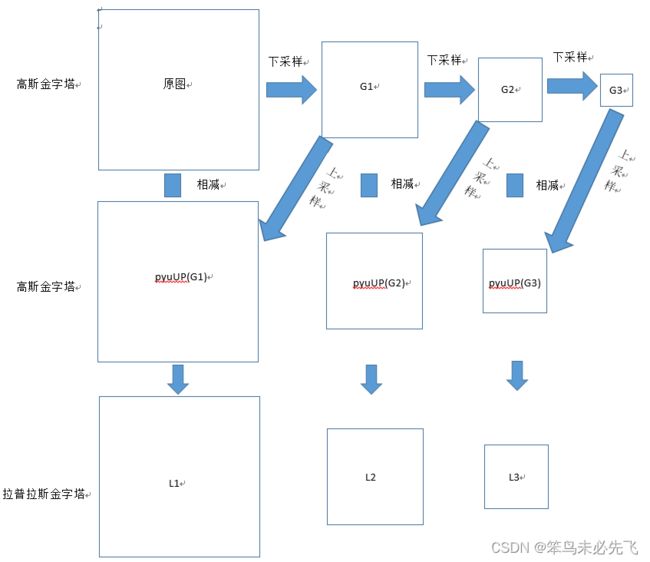
高斯金字塔

上一层的每个像素值等于下一层图像中5个像素的高斯加权平均值，这样操作一次，MxN的图像就变为M/2 x n/2 ，连续这样操作我们得到一个分辨率不断下降的图像金字塔。

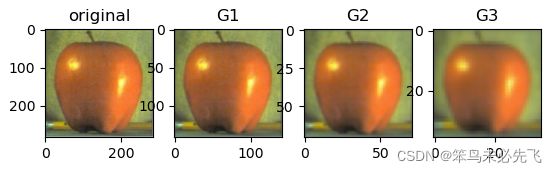
1、cv.pyrDown()函数

从一个高分辨率大尺寸的图像向上构建一个金字塔，尺寸变小，分辨率降低。

如果输入图像的高宽是偶数，那么输出图像的高宽 = 输入图像的高宽 /2 ，如果是奇数，则输出图像的高宽 = （输出图像的高宽 + 1） / 2

import cv2
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
img = cv2.imread("./apple.png")
lower_pyramid = img

#显示图片
plt.subplot(1,4,1)
#将图像BGR格式转换为RGB格式
plt.imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB))
plt.title("original")

#三次向下采样
for i in range(3):
    lower_pyramid = cv2.pyrDown(lower_pyramid)
    plt.subplot(1,4,i + 2)
    plt.imshow(cv2.cvtColor(lower_pyramid,cv2.COLOR_BGR2RGB))
    plt.title(f"G{i + 1}")
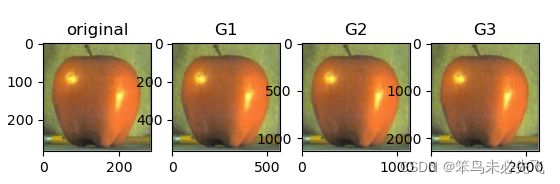
plt.show()

2、cv2.pyrUp()函数

从一个低分辨率小尺寸的图像向上构建一个金字塔，尺寸变大，但分辨率不会增加。输出图像的大小 = 输入图像的大小 * 2

import cv2
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator
img = cv2.imread("./apple.png")
lower_pyramid = img

#显示图片
plt.subplot(1,4,1)
#将图像BGR格式转换为RGB格式
plt.imshow(cv2.cvtColor(img,cv2.COLOR_BGR2RGB))
plt.title("original")

#三次向上采样
for i in range(3):
    lower_pyramid = cv2.pyrUp(lower_pyramid)
    plt.subplot(1,4,i + 2)
    plt.imshow(cv2.cvtColor(lower_pyramid,cv2.COLOR_BGR2RGB))
    plt.title(f"G{i + 1}")
plt.show()

拉普拉斯金字塔

拉普拉斯金字塔是由高斯金字塔计算得来的。拉普拉斯金字塔的图像看起来就像是边界图，其中很多像素都是0。

 

将图片扩展到288的原因

如果原图像的大小是奇数，例如(121,121)，那么缩小一次后图像的大小为(61,61)，用(61,61)的图像进行一次放大后的图像大小为（122,122）与原图像大小不一样，无法进行减法运算。

在demo中，图像大小是(288,288)，下采样5次，每次的大小为(144,144)，(72,72)，(36,36)，(18,18)。每次下采样后的图像大小都是偶数，这样在经过上采样后的大小就会与原图向大小相同。