深度学习基础入门（二）：初始化、调参、优化

一、初始化

权值初始化对网络优化至关重要。早年深度神经网络无法有效训练的一个重要原因就是早期人们对初始化不太重视。

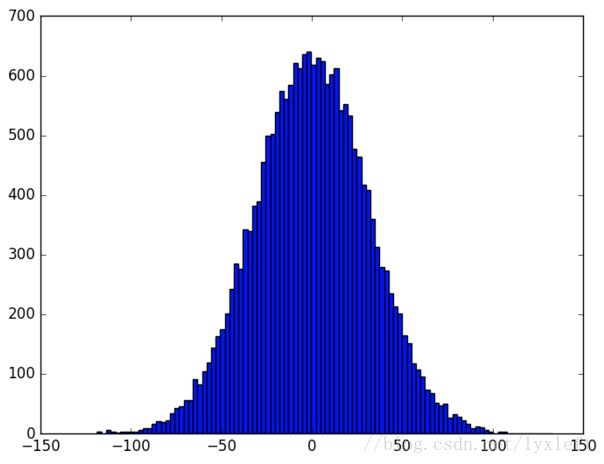
        如何理解权值的初始化非常重要？对于新手而言，我们可以按照自己的理解，随意取个初始化的方法，比如，假设现在输入层有1000个神经元，隐藏层有1个神经元，输入数据x为一个全为1的1000维向量，采取高斯分布来初始化权重矩阵w，偏置b取0。令w服从均值为0、方差为1的正太分布，x全为1，b全为0，输入层一共1000个神经元，所以输出的y服从的是一个均值为0、方差为1000的正太分布。生成20000万个y并查看其均值、方差以及分布图像：

上一节我们讲过，激活函数中常用的一种，sigmoid，如果忘了请回顾一下。从分布中可见，y有可能是一个远小于-1或者远大于1的数，通过激活函数（比如sigmoid）后所得到的输出会非常接近0或者1，也就是隐藏层神经元处于饱和的状态。所以当出现这样的情况时，在权重中进行微小的调整仅仅会给隐藏层神经元的激活值带来极其微弱的改变。而这种微弱的改变也会影响网络中剩下的神经元，然后会带来相应的代价函数的改变。结果就是，这些权重在我们进行梯度下降算法时会学习得非常缓慢。所以，让输出y处在0附近，即均值|y|≈0，效果最佳。从这个例子可见一斑，我们为什么要进行权重的初始化操作。

        我们介绍几个适用于深度神经网络的初始化方法。

        初始化的基本思想：方差不变，即设法对权值进行初始化，使得各层神经元的方差保持不变，从而不会发生前向传播爆炸和反向传播梯度消失等问题。

        Xavier初始化 最常用的初始化权重的方法。最简单的一种形式的，从高斯分布或均匀分布中对权值进行采样，使得权值的方差是1/n，其中n是输入神经元的个数。该推导假设激活函数是线性的。还有进化版本的：

        Xavier初始化的原理推导可参见这篇博文:http://blog.csdn.net/shuzfan/article/details/51338178

        需要注意的是，Xavier推导的时候假设激活函数是线性的，显然我们目前常用的ReLU和PReLU并不满足这一条件。

        He初始化/MSRA初始化 从高斯分布或均匀分布中对权值进行采样，使得权值的方差是2/n。该推导假设激活函数是ReLU。因为ReLU会将小于0的神经元置零，大致上会使一半的神经元置零，所以为了弥补丢失的这部分信息，方差要乘以2。试验表明在网络加深后，MSRA初始化明显优于Xavier初始化。

        其具体推导：http://blog.csdn.net/shuzfan/article/details/51347572

        批量规范化（batch-normalization，BN） 每层显式地对神经元的激活值做规范化，使其具有零均值和单位方差。批量规范化使激活值的分布固定下来，这样可以使各层更加独立地进行学习。批量规范化可以使得网络对初始化和学习率不太敏感。此外，批量规范化有些许正则化的作用，但不要用其作为正则化手段。

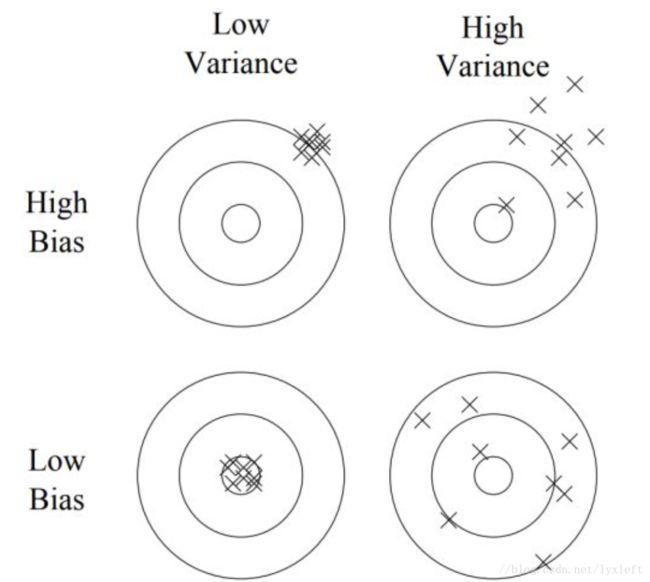
        关于偏差和方差：

        偏差 偏差度量了网络的训练集误差和贝叶斯误差（即能达到的最优误差）的差距。高偏差的网络有很高的训练集误差，说明网络对数据中隐含的一般规律还没有学好。当网络处于高偏差时，通常有以下几种解决方案。1. 训练更大的网络。网络越大，对数据潜在规律的拟合能力越强。2. 更多的训练轮数。通常训练时间越久，对训练集的拟合能力越强。3. 改变网络结构。不同的网络结构对训练集的拟合能力有所不同。

        方差 方差度量了网络的验证集误差和训练集误差的差距。高方差的网络学习能力太强，把训练集中自身独有的一些特点也当作一般规律学得，使网络不能很好的泛化（generalize）到验证集。当网络处于高方差时，通常有以下几种解决方案。1. 更多的数据。这是对高方差问题最行之有效的解决方案。2. 正则化。3. 改变网络结构。不同的网络结构对方差也会有影响。

 

 

二、调参

      参数其实是个比较泛化的称呼，因为它不仅仅包括一些数字的调整，它也包括了相关的网络结构的调整和一些函数的调整，除了我们耳熟能详的学习率、衰减函数等，还可以是层数、节点数、特征标准化操作等等。调参有两个直接的目的：1. 当网络出现训练错误的时候，我们自然需要调整参数。 2. 可以训练但是需要提高整个网络的训练准确度。

      我们常用的调参技巧有：

        随机搜索 ： 由于你事先并不知道哪些超参数对你的问题更重要，因此随机搜索通常是比网格搜索（grid search）更有效的调参策略。但我感觉随机搜索在实践应用中，就是暴力搜索+微调，即胡乱暴力调整到一个还可以的结果基础上，在其附近进行微调。

        对数空间搜索 ：对于隐层神经元数目和层数，可以直接从均匀分布采样进行搜索。而对于学习率、L2正则化系数、和动量，在对数空间搜索更加有效。

        但是最好的方式还是针对问题来调参。我觉得参考文献【6】经验总结得非常好。

三、优化

        在网络结构确定之后，我们需要对网络的权值（weights）进行优化。

梯度下降（gradient descent，GD）

        梯度下降法是求解目标函数极值的最常用的优化方法之一。其基本原理非常简单：沿着目标函数梯度下降的方向搜索极小值。

        想象你去野足但却迷了路，在漆黑的深夜你一个人被困住山谷中，你知道谷底是出口但是天太黑了根本看不清楚路。于是你确定采取一个贪心(greedy)算法：先试探在当前位置往哪个方向走下降最快（即梯度方向），再朝着这个方向走一小步，重复这个过程直到你到达谷底。这就是梯度下降的基本思想。

        梯度下降算法的性能大致取决于三个因素。1. 初始位置。如果你初始位置就离谷底很近，自然很容易走到谷底。2. 山谷地形。如果山谷是“九曲十八弯”，很有可能你在里面绕半天都绕不出来。3. 步长。你每步迈多大，当你步子迈太小，很可能你走半天也没走多远，而当你步子迈太大，一不小心就容易撞到旁边的悬崖峭壁，或者错过了谷底。

误差反向传播（error back-propagation，BP）

        结合微积分中链式法则和算法设计中动态规划思想用于计算梯度。 直接用纸笔推导出中间某一层的梯度的数学表达式是很困难的，但链式法则告诉我们，一旦我们知道后一层的梯度，再结合后一层对当前层的导数，我们就可以得到当前层的梯度。动态规划是一个高效计算所有梯度的实现技巧，通过由高层往低层逐层计算梯度，避免了对高层梯度的重复计算。

滑动平均（moving average）

        要前进的方向不再由当前梯度方向完全决定，而是最近几次梯度方向的滑动平均。利用滑动平均思想的优化算法有带动量（momentum）的SGD、Nesterov动量、Adam（ADAptive Momentum estimation）等。

自适应步长

        自适应地确定权值每一维的步长。当某一维持续震荡时，我们希望这一维的步长小一些；当某一维一直沿着相同的方向前进时，我们希望这一维的步长大一些。利用自适应步长思想的优化算法有AdaGrad、RMSProp、Adam等。

学习率衰减

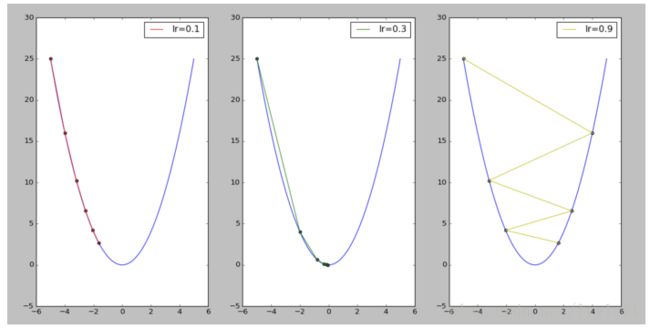
        如何调整搜索的步长（也叫学习率，Learning Rate）、如何加快收敛速度以及如何防止搜索时发生震荡却是一门值得深究的学问。当开始训练时，较大的学习率可以使你在参数空间有更大范围的探索；当优化接近收敛时，我们需要小一些的学习率使权值更接近局部最优点。

        如果学习率过大，最右图所示，可能会发生震荡。

深度神经网络优化的困难

        有学者指出，在很高维的空间中，局部最优是比较少的，而大部分梯度为零的点是鞍点。平原区域的鞍点会使梯度在很长一段时间内都接近零，这会使得拖慢优化过程。

四、实现技巧

        图形处理单元（graphics processing units, GPU） 深度神经网络的高效实现工具。简单来说，CPU擅长串行、复杂的运算，而GPU擅长并行、简单的运算。深度神经网络中的矩阵运算都十分简单，但计算量巨大。因此，GPU无疑具有非常强大的优势。python中的深度学习包可以调用GPU进行运算，这一点比Matlab好很多。目前很多入门者只会使用matlab，而matlab用于普通神经网络入门上手还是体验比较好的，做性能要求高的深度神经网络的话还是考虑学习学习python。后面会放一些python学习笔记。

        向量化（vectorization） 代码提速的基本技巧。能少写一个for循环就少写一个，能少做一次矩阵运算就少做一次。实质是尽量将多次标量运算转化为一次向量运算；将多次向量运算转化为一次矩阵运算。因为矩阵运算可以并行，这将会比多次单独运算快很多。

 

参考文献：

【1】https://zhuanlan.zhihu.com/p/31561570

【2】https://www.cnblogs.com/makefile/p/init-weight.html?utm_source=itdadao&utm_medium=referral

【3】https://www.jianshu.com/p/03009cfdf733

【4】 www.neuralnetworksanddeeplearning.com，第三章

【5】https://www.jianshu.com/p/d8222a84613c

【6】http://blog.csdn.net/qq_20259459/article/details/70316511