最新论文笔记(+16):K-Time Modifiable and Epoch-Based Redactable Blockchain / TIFS 2021
K-Time Modifiable and Epoch-Based Redactable Blockchain(k次修改和基于epoch的可编辑区块链)
这篇文章是今年发表在TIFS上的一篇区块链相关论文,感觉写的非常好,收获颇丰,以下是我个人读后感或学习笔记吧。这里先说一下本人读完该篇论文的感受,以便后面读者能重点理解或仔细阅读的地方:
- 1)本篇文章还是比较推荐阅读的(如果是相关研究方向),整体的架构或思路非常清晰,介绍的也非常详细。(毕竟是TIFS的文章啊哈哈哈)
- 2)个人感觉文章最巧妙的地方是将变色龙哈希的陷门密钥公开,而安全性由数字签名(ECDSA)和抗碰撞哈希来保证,与其他相关文章不同。还有其他巧妙的地方留给读者自己发掘吧。
- 3)另外就是CA授予修改者k次重写的权限和基于epoch时间期限这两个关键点,和惩罚措施,都是论文的创新点。
话不多说,下面将大致按照文章结构内容,并结合自己读后的学习笔记进行梳理和归纳,可能会有整理不当的地方,仅代表个人理解,详细内容还是建议看原文!
- 原文链接:K-Time Modifiable and Epoch-Based Redactable Blockchain
文章目录预览
-
- K-Time Modifiable and Epoch-Based Redactable Blockchain(k次修改和基于epoch的可编辑区块链)
- 一、写作背景及内容贡献
-
- 1.1 写作背景
- 1.2 内容贡献
- 二、主要内容
-
- 2.1 预备知识
-
- 2.1.1 变色龙哈希(CH)
- 2.1.2 数字签名(DS)
- 2.2 链参与者及职责
- 2.3 系统模型
- 2.4 安全模型
-
- 2.4.1 EUF-CMA安全(存在不可伪造的选择消息攻击)
- 2.4.2 w-KE安全(弱密钥提取安全模型)
- 2.5 性能分析
- 三、总结
一、写作背景及内容贡献
1.1 写作背景
首先,文章简要的介绍了下传统不可变区块链的发展历程和发展状况;其次,提到了目前还存在的一些问题;然后,介绍了当前的一些解决方案;最后,引出了本文的主要工作。
Puddu等人提出了μ链,通过将区块链交易结构改进为可变结构,以实现后续对交易的添加。但是,这种方法不切实际,开销很大,链的参与者之间有多个交互。
Florian等人引入了一种新颖的数据擦除方法,但原始交易是不可变的,完整节点保留所有原始区块。
Ateniese等人最早引入可编辑区块链的概念,提供了一个增强的变色龙哈希的粗细粒度级控制和PKI的的区块级重写。
Derler等人为了灵活管理重写权限,提出了一个可编辑区块链,通过变色龙哈希和邻时陷门和基于密文策略属性控制的交易级重写方案。
Deuber等人提出了一个区块级可编辑区块链(可消除CA),并通过基于共识的投票实现了编辑功能。但不诚实和理性的矿工可能不会坚持候选区块编辑池,且容易共谋或编辑请求成本不够高的话,容易受到DDoS攻击
因此,基于以上相关的工作,文章提出了为限定修改者的编辑权限和惩罚恶意行为,引入了k次可修改、基于epoch的可编辑区块链——KERB。相关方案的对比:
1.2 内容贡献
主要贡献:
- 1)k次修改器:为减少恶意行为,修改权限被CA定义为最多限制k次,若发生超过k次的交易修改时,CA处理罚款。
- 2)基于epoch编辑:为惩罚恶意行为,每个修改者需定时存保证金。在授权期限内,若发生恶意行为,CA可以使用自身密钥和修改者的密钥提取存款。
- 3)强大的安全模型:允许交易所有者和修改者之间的勾结来改进Ateniese和Derler中引入的安全模型。本文使用更通用的变色龙哈希,而不是增强变色龙哈希和CHET。没有陷门正确性检查的需求,数字签名来支持重写特权,而不是加密机制,以获得最佳性能,适用于大型环境,成本小。
二、主要内容
2.1 预备知识
2.1.1 变色龙哈希(CH)
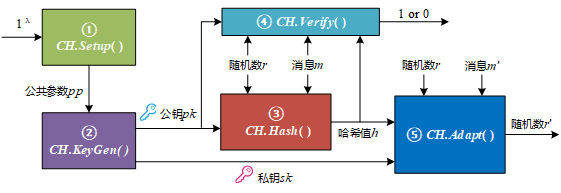
变色龙哈希的定义是指:任何拥有陷门的参与者都可以广义的找到哈希碰撞,使得 C H . H a s h ( m ) = C H . H a s h ( m ′ ) CH.Hash(m) = CH.Hash(m') CH.Hash(m)=CH.Hash(m′)(具体定义见变色龙哈希介绍)。CH函数的消息空间 M M M由5个算法 S e t u p , K e y G e n , H a s h , V e r i f y , A d a p t {Setup, KeyGen, Hash, Verify, Adapt} Setup,KeyGen,Hash,Verify,Adapt构成。
- 1) C H . S e t u p ( 1 λ ) → p p CH.Setup(1^\lambda)\to pp CH.Setup(1λ)→pp
- 2) C H . K e y G e n ( p p ) → ( s k , p k ) CH.KeyGen(pp)\to (sk,pk) CH.KeyGen(pp)→(sk,pk)
- 3) C H . H a s h ( p k , m , r ) → h CH.Hash(pk,m,r)\to h CH.Hash(pk,m,r)→h
- 4) C H . V e r i f y ( p k , m , h , r ) → b CH.Verify(pk,m,h,r)\to b CH.Verify(pk,m,h,r)→b
- 5) C H . A d a p t ( s k , m , h , r , m ′ ) → r ′ CH.Adapt(sk,m,h,r,m')\to r' CH.Adapt(sk,m,h,r,m′)→r′
这5个算法的关系可以大致从以下图可以看出相应的流程关系(为方便理解,本人画了个大概流程):
2.1.2 数字签名(DS)
数字签名的定义指:签名者用自己的私钥进行签名,然后任何人都可以用他的公钥进行认证,具有不可伪造和不可否认性。
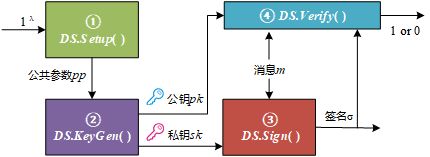
DS的消息空间 M M M由4个算法 S e t u p , K e y G e n , S i g n , V e r i f y {Setup, KeyGen, Sign, Verify} Setup,KeyGen,Sign,Verify构成。
- 1) D S . S e t u p ( 1 λ ) → p p DS.Setup(1^\lambda)\to pp DS.Setup(1λ)→pp
- 2) D S . K e y G e n ( p p ) → ( s k , p k ) DS.KeyGen(pp)\to (sk,pk) DS.KeyGen(pp)→(sk,pk)
- 3) D S . S i g n ( s k , m ) → σ DS.Sign(sk,m)\to \sigma DS.Sign(sk,m)→σ
- 4) D S . V e r i f y ( p k , σ , m ) → b DS.Verify(pk,\sigma,m)\to b DS.Verify(pk,σ,m)→b
这4个算法的关系可以大致从以下图可以看出相应的流程关系(为方便理解,本人画了个大概流程):
2.2 链参与者及职责
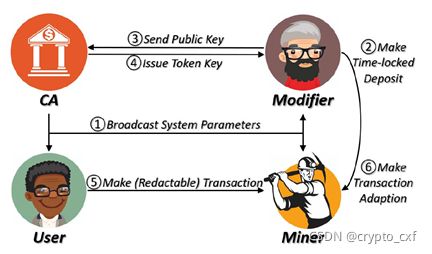
- 1)CA:代表区块链管理者,主要复制初始化系统,并广播参数,检查修改者时间锁定存款的有效性,并颁发k次修改特权,若修改者违反k次修改特权,CA可在到期前提取存款。
- 2)修改者:可以进行时间锁定存款的链参与者,具有CA颁发的修改特权,若发生任何不当行为,将失去押金。
- 3)用户:是链的参与者,生成不能修改的不可变交易,生成允许修改者编辑的可编辑交易。
- 4)矿工:验证和添加交易的链参与者,用来维护区块,并相互链接,形成一条链。
2.3 系统模型
KERB的工作流程只要包括系统初始化、交易生成、交易验证和恶意惩罚四个阶段。
-
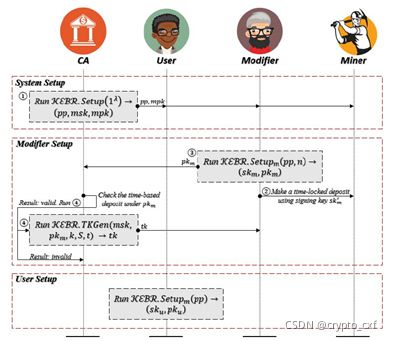
1)系统初始化:如下图所示,细分为系统设置,修改者设置和用户设置。
- 系统设置:CA运行 K E R B . S e t u p ( 1 λ ) KERB.Setup(1^\lambda) KERB.Setup(1λ)算法,生成公共参数 p p pp pp、主密钥 m s k msk msk和主公钥 m p k mpk mpk。
- 修改者设置:每个修改者从CA收到公共参数后,运行 K E R B . S e t u p m ( p p , n ) KERB.Setup_m(pp,n) KERB.Setupm(pp,n)算法,生成 s k m , p k m sk_m,pk_m skm,pkm。修改者进行时间锁定 t t t的保证金,它可以在到期前与CA和修改者签署的签名一起支付。然后,修改者将 p k m pk_m pkm发送给CA,CA指定修改操作次数k和修改者的属性集S,运行token密钥生成算法 K E R B . T K G e n ( ) KERB.TKGen() KERB.TKGen()生成token和ti,并将tk发送给修改者。
- 用户设置:每个用户从CA收到公共参数后,运行 K E R B . S e t u p u ( p p ) KERB.Setup_u(pp) KERB.Setupu(pp)算法,生成 s k u , p k u sk_u,pk_u sku,pku。
-
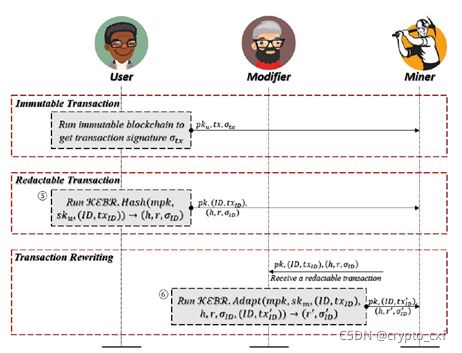
2)交易生成:如下图所示,每个用户都允许创建两种类型的交易,可编辑交易可以由指定的修改者修改。
- 不可变交易:每个用户都可以像传统不可变区块链一样创建不可变交易。用户使用自己的密钥 s k u sk_u sku和传统哈希函数生成交易 t x tx tx及其签名 σ t x \sigma_{tx} σtx。然后,用户广播公钥 p k u pk_u pku(此处应该是排版错误,应为 p k u pk_u pku,而不是 p k m pk_m pkm)、交易 t x tx tx和签名 σ t x \sigma_{tx} σtx到区块链生态系统中。
- 可编辑交易:每个用户都可以通过运行散列算法 K E R B . H a s h ( ) KERB.Hash() KERB.Hash()来创建可编辑的交易,使用指定访问结构A(记住这个访问结构,本人理解应该也是访问策略,与最后实验提到的策略长度一个意思,它是一个字符串)生成 ( h , r , σ I D ) (h,r,\sigma_{ID}) (h,r,σID)。用户将公钥 p k u pk_u pku、交易 ( I D , t x I D ) (ID,tx_{ID}) (ID,txID)和签名 ( h , r , σ I D ) (h,r,\sigma_{ID}) (h,r,σID)发送到区块链生态系统。
-
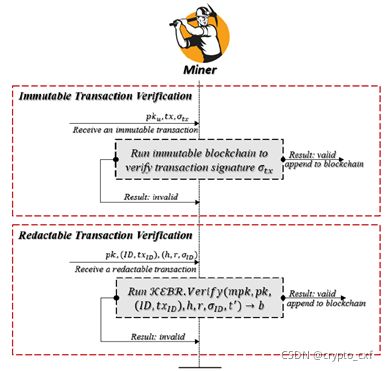
3)交易验证:如下图所示,区块链生态系统广播了两种类型的交易。因此,也有两种类型的验证,不可变交易的验证和可编辑交易的验证。
- 不可变交易验证: 在收到一个与用户公钥 p k u pk_u pku、交易 t x tx tx和签名 σ t x \sigma_{tx} σtx相关联的不可变交易后,矿工通过运行不可变区块链验证过程,若交易有效则将其附加到一个新区块中,否则拒绝。
- 可编辑交易验证:在接收到一个与公钥 p k = ( p k u , p k m , t k ) pk=(pk_u,pk_m,tk) pk=(pku,pkm,tk)、交易 ( I D , t x I D ) (ID,tx_{ID}) (ID,txID)和签名 ( h , r , σ I D ) (h,r,\sigma_{ID}) (h,r,σID)相关联的可编辑交易后,矿工通过运行验证算法 K E R B . V e r i r y ( ) KERB.Veriry() KERB.Veriry()来验证交易。若交易有效,矿工将重写该交易的本地副本,否则拒绝。
-
4)恶意惩罚:如下图所示,这个阶段包括两个子阶段,签名密钥提取和货币惩罚。
- 签名密钥提取:为简单起见,假设一个矿工检测到一个修改者的恶意行为(例如,发生了冲突的编辑),矿工则允许提取算法 K E R B . E x ( ) KERB.Ex() KERB.Ex()去获取秘密签名密钥 s k m ′ sk_{m'} skm′。矿工发送秘密签名密钥 s k m ′ sk_{m'} skm′和矿工公钥 p k m i n e r pk_{miner} pkminer给CA。
- 货币惩罚:CA接收到参数后,生成一个交易来提取时间锁定的存款,并将奖励发送给矿工。注意,CA由秘密密钥 s k c sk_c skc(主密钥 m s k msk msk?)和矿工的私密签名密钥 s k m ′ sk_{m'} skm′,它可以到期前提取定时的保证金。
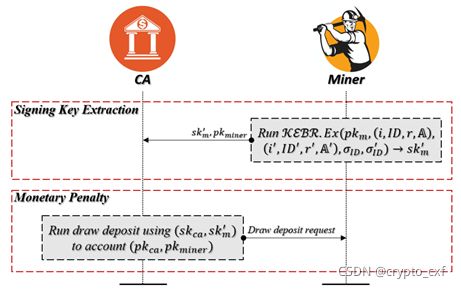
值得注意的是,文章中假设CA是完全可信的,矿工大多数都是诚实的,用户和修改者是不受信任,他们可以一起合谋攻击。
2.4 安全模型
本文中,变色龙哈希的陷门是公开的,系统的安全性依赖于数字签名和抗碰撞哈希的安全性。因此无需考虑变色龙哈希的不可区分性、外部抗碰撞性和内部抗碰撞性。因此,文章提出了两种类型的安全定义:
2.4.1 EUF-CMA安全(存在不可伪造的选择消息攻击)
定义EUF-CMA安全. 令 O O O表示谕言机集,则有设置谕言机 O S e t u p ( ⋅ ) O_{Setup}(·) OSetup(⋅),腐败谕言机 O C o r r u p t ( ⋅ ) O_{Corrupt}(·) OCorrupt(⋅),token密钥生成谕言机 O T K G e n ( ⋅ ) O_{TKGen}(·) OTKGen(⋅),hash谕言机 O H a s h ( ⋅ ) O_{Hash}(·) OHash(⋅)和自适应谕言机 O A d a p t ( ⋅ ) O_{Adapt}(·) OAdapt(⋅)。若对于任何概率多项式时间敌手A,以下优势是可忽略的,则说明KERB是EUF-CMA安全的:
A d v A , K E R B E U F − C M A ( 1 λ ) = P r [ E x p A , K E R B E U F − C M A ( 1 λ ) = 1 ] Adv^{EUF-CMA}_{A,KERB}(1^\lambda)=Pr[Exp^{EUF-CMA}_{A,KERB}(1^\lambda)=1] AdvA,KERBEUF−CMA(1λ)=Pr[ExpA,KERBEUF−CMA(1λ)=1]
Proof: 假设存在一个概率多项式时间敌手A,它可以以不可忽略的优势打破EUF-CMA模型中的KERB,然后,构建一个模拟器B来破解底层数字签名方案C,具有不可忽略的优势。安全证明的证明思想如下:
- A。初始设置:模拟器B根据签名方案C提供的参数,初始化一些CH的公共参数,然后将其返回给敌手A,并生成一组列表值。
- B。查询阶段:敌手A自适应查询相关的谕言机模型,包括 O S e t u p m ( ⋅ ) 、 O C o r r u p t m ( ⋅ ) 、 O S e t u p u ( ⋅ ) 、 O C o r r u p t u ( ⋅ ) 、 O T K G e n ( ⋅ ) 、 O H a s h ( ⋅ ) 、 O A d a p t ( ⋅ ) O_{Setup_{m}}(·)、O_{Corrupt_m}(·)、O_{Setup_{u}}(·)、O_{Corrupt_u}(·)、O_{TKGen}(·)、O_{Hash}(·)、O_{Adapt}(·) OSetupm(⋅)、OCorruptm(⋅)、OSetupu(⋅)、OCorruptu(⋅)、OTKGen(⋅)、OHash(⋅)、OAdapt(⋅)。
- C。输出:若敌手A输出一个元组满足某个特定条件,则它能够通过验证 K E R B . V e r i f y ( ) = 1 KERB.Verify()=1 KERB.Verify()=1。从而可知模拟器B能破解签名方案C所模拟的底层数字签名方案,因此它的优势是可忽略的,得证。即 A d v A , K E R B E U F − C M A ( 1 λ ) = A d v C , D S E U F − C M A ( 1 λ ) Adv^{EUF-CMA}_{A,KERB}(1^\lambda)=Adv^{EUF-CMA}_{C,DS}(1^\lambda) AdvA,KERBEUF−CMA(1λ)=AdvC,DSEUF−CMA(1λ)
详细的步骤就不再赘述了。(证明过程太长了,建议看原文。。。)
2.4.2 w-KE安全(弱密钥提取安全模型)
定义 w-KE安全. 如果对于任何概率多项式时间敌手A,以下优势是可忽略的,则说明KERB是w-KE安全的: A d v A , K E R B w − K E ( 1 λ ) = P r [ E x p A , K E R B w − K E ( 1 λ ) = 1 ] Adv^{ w-KE}_{A,KERB}(1^\lambda)=Pr[Exp^{ w-KE}_{A,KERB}(1^\lambda)=1] AdvA,KERBw−KE(1λ)=Pr[ExpA,KERBw−KE(1λ)=1]
Proof: 假设存在一个概率多项式时间敌手A,它可以在w-KE安全模型中以不可忽略的优势打破KERB。然后,构建了一个模拟器B可以打破DDH C S D D H C_{S_{DDH}} CSDDH的稳健性或哈希函数 C h C_h Ch的抗碰撞性,具有不可忽略的优势。安全证明的证明思想如下:
- A。初始设置:模拟器B初始化DS和CH 的公共参数 p p D S 、 p p C H 、 D S pp_{DS}、pp_{CH}、DS ppDS、ppCH、DS密钥对和CH 密钥对,并返回 p p D S , p p C H pp_{DS}, pp_{CH} ppDS,ppCH给敌手A。
- B。查询阶段:敌手A自适应地查询相关的谕言机模型,包括 O T K G e n ( ⋅ ) 、 O H a s h ( ⋅ ) O_{TKGen}(·)、O_{Hash}(·) OTKGen(⋅)、OHash(⋅)。(与EUF-CMA安全相比,w-KE安全模型允许A破坏所有用户和修改者,因此无需用户和修改者的相关谕言机O)
- C。输出:若敌手A输出一个元组,它能够通过验证过程,并且没有人可以提取秘密签名密钥。从而可知B能够打破DDH C S D D H C_{S_{DDH}} CSDDH的稳健性或哈希函数 C h C_h Ch的抗碰撞性,即满足如下: A d v A , K E R B w − K E ( 1 λ ) = ϵ S D D H Adv^{w-KE}_{A,KERB}(1^\lambda)=\epsilon_{S_{DDH}} AdvA,KERBw−KE(1λ)=ϵSDDH和 A d v A , K E R B w − K E ( 1 λ ) = ϵ h Adv^{w-KE}_{A,KERB}(1^\lambda)=\epsilon_h AdvA,KERBw−KE(1λ)=ϵh
2.5 性能分析
- 1)实验环境:一台64位windows 10 2.9GHz Inter® Core™ i7-7820HK CPU的PC机。
- 2)KERB实例化:椭圆曲线数字签名算法(ECDSA)和变色龙哈希作为基本构建块。
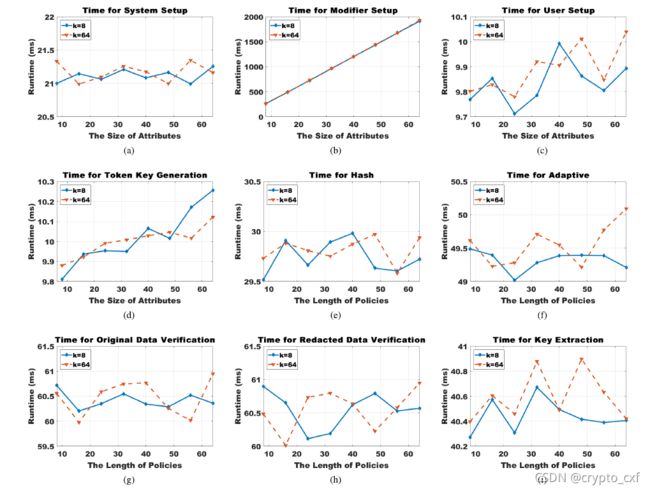
从图中可知,无论涉及多少属性和编辑次数,系统都是稳定的,且编辑次数k对最终效率几乎不影响。
但个人感觉实验还是有点少,意犹未尽的感觉。
三、总结
本篇文章是基于传统不可变区块链中可能存储了一些违法内容,且“被遗忘权”的数据监管要求等问题,引入了新的可编辑区块链来以可控的方式使其能够有权限的编辑。但是同样带来新的问题,一旦参与者被授权重写权限,它可以修改任何内容而不会因恶意行为遭受惩罚。因此,本文引入了一个k次可修改和基于epoch的可编辑区块链——KERB,带有货币惩罚来控制重写的权限和惩罚恶意行为。最终的实验分析表明,此解决方案是比较先进的,具有更优越的功能和性能。