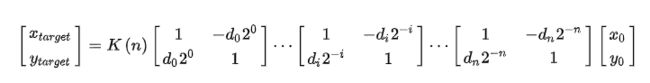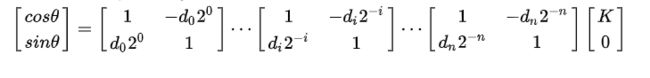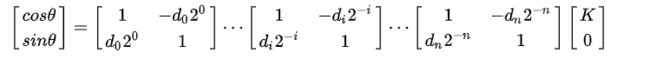基于FPGA实现经过Matalb验证的CORDIC算法——旋转模式（给定旋转角计算旋转后的坐标）和向量模式

前言

FPGA能容易地实现加减运算，但是计算三角函数或者指数、对数、平方根等很复杂。一般这些复杂函数的计算，会通过查找表或者近似计算（泰勒展开）等技术在FPGA上实现。【查找表方法：比如说要计算三角函数，就可以先采用三角函数基本公式以及和差化积等公式将函数值求出，建立查找表，将求出后的数值存在内存中，需要该数值时进行寻址；泰勒级数展开：会涉及到很多乘除法以及浮点数问题，运算复杂且影响精度】

CORDIC（坐标旋转数字计算方法）算法由J.D.Volder提出，相当于是一个“移位相加“算法，该算法用基本的加减或者移位运算来代替乘法运算，逐渐与目标值逼近，从而最终得到函数的解。另外该算法分别可以在圆坐标系、线性坐标系和双曲线坐标系使用。

CORDIC算法有两种工作模式：旋转模式和向量模式，旋转模式是给定旋转角，计算旋转后的坐标，而向量模式相当于旋转模式的变体（倒推得到），根据旋转后的坐标，得到向量的角度和模值。

因此采用CORDIC算法后，函数就能采用FPGA进行简易地处理，下面主要讲解旋转模式。

旋转模式

首先根据旋转模式下的圆坐标系进行分析学习
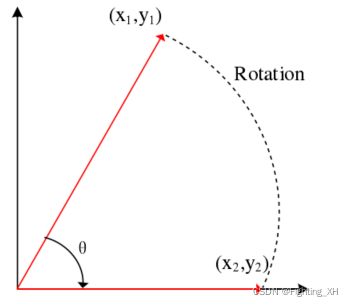
根据下图我们可以进行旋转公式推导

该图展示的是从红色旋转到蓝色，因此根据三角关系即可得到如下旋转数学仿真：

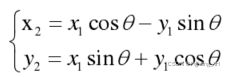
写成旋转矩阵形式：

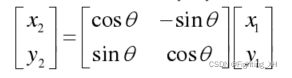
还可以提取cosθ，便于写成tanθ的形式，写成tanθ后就可以转换成2的次幂形式。

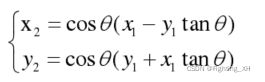
cosθ可以作为伸缩因子，将其去掉，我们就能得到CORDIC的伪旋转，对于伪旋转来说，旋转的角度不变，但是由于除去了cosθ，相当于xy的值乘以了cosθ的倒数，cosθ的倒数 > 1 ，因此向量的模值在旋转的过程中会变大，后续我们会引入参数进行补偿（K）。

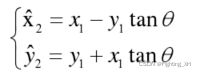
2的次幂形式转换：


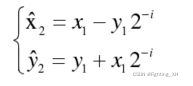
举例：当逆时针旋转90度的时候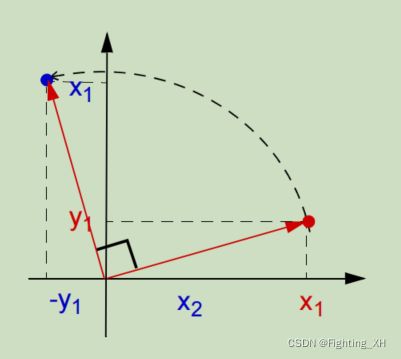
可得到如下的矩阵变换：

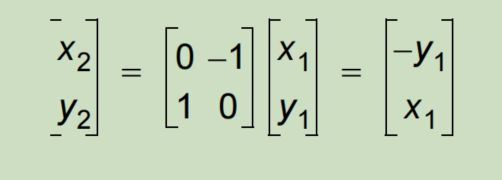
至此，我们就介绍完了旋转的几何原理，该算法就是已知一点坐标以及旋转角度，我们即可求出旋转后点的坐标。此时就涉及到了求取三角函数值的问题，并不适用于FPGA实现，于是采用CORDIC算法进行简化，将三角函数运算转换成移位加法运算。

CORDIC算法原理

该算法主要包括以下几点：
1、将旋转角度θ分成若干个固定大小的角度θi（θ0-θi），同时θi满足如下的公式，可看出已经将正切函数部分转换成了移位操作。（除以i个2，相当于右移i位）。

2、同时θ 的范围是【-π/2，π/2】，其余超出的角度我们给与一个方向值d来判断角度，也称为符号判决因子，如果旋转角已经大于θ，则di = -1，表示顺时针旋转；如果旋转角已经小于θ，则di = 1，表示旋转为逆时针。因此其每次旋转的角度值为 di*θi，最终得到每次迭代的旋转表达式：

如下为角度累加器的公式，z为角度叠加值，d为旋转方向

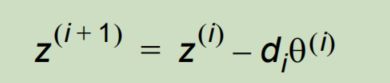
3、迭代操作得到增益K值

因此当我们进行第一次旋转的时候：（θ0角的旋转方向为d0）

x1 = cosθ0(x0 – d0y0tanθ0)
y1 = cosθ0(y0 + d0x0tanθ0)

第二次旋转的时候：(将上面的x1 和 y1 代入并提取cosθ)

x2 = cosθ1(x1 – d1y1tanθ1) = cosθ1cosθ0(x0 – d0y0tanθ0 – d1y0tanθ1 –d1d0 x0tanθ1 tanθ0)
y2 = cosθ1(y1 + d1x1tanθ1) = cosθ1cosθ0(y0 +d0x0tanθ0 + d1x0tanθ1 – d1d0y0tanθ1 tanθ0)

当进行到第n次旋转，即可得到n个cos相乘，我们将其规定为K（增益），当i的次数很大时，K的值趋于一个常数。K的数值需要根据迭代次数来确定，同时迭代次数确定后，k的值也能确定出来，我们就可以将这个误差值K预先存储下来，迭代结束后就可以对旋转后的xy进行补偿校正。
由于如下公式以及tanθi = 2^(-i)

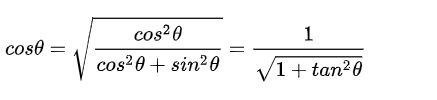
则

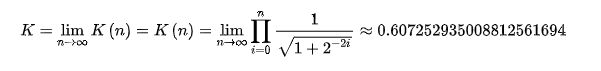
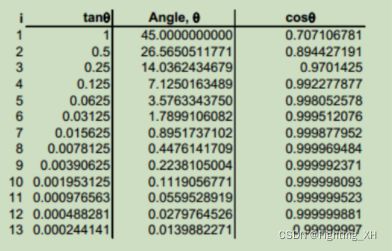
4、把所有tanθi = 2^(-i)对应的旋转角度和正切值制成一张表如下，便于存储为查找表。
于是任意的旋转角θ，都能由下表的不同θi进行多次累加旋转得到。

CORDIC算法最终公式

经过CORDIC算法原理分析以及推导，我们可以得到最终的公式：
通过下面公式可看出，对应三角函数运算转化为了基本的加减和移位运算。
补充：当计算向量模值的时候，角度累加器Z 可忽略，只用前两个公式即可。

当FPGA进行计算的时候，每次迭代运算需要需要步骤：

1次查表【每次迭代都会有一个相对固定角度的累加，这个角度就是公式中2^(-i)对应的角度值，一个i对应一个角度值，用查找表实现】
三次加法【xyz的累加】
2次移位（每迭代一次，xy要分别进行一次移位）

---

最终公式的数学矩阵形式：

通常简化操作如下：

Matlab实现CORDIC算法（旋转模式）

close all;
clear;
clc;
% 初始化
die = 16;     %迭代次数
x = zeros(die+1,1);
y = zeros(die+1,1);
z = zeros(die+1,1);
x(1) = 0.607253;   %初始设置
z(1) = pi/6;    %待求角度θ
%迭代操作
for i = 1:die
    if z(i) >= 0% 判断旋转角度是逆时针还是顺时钟
        d = 1;  % 逆时针
    else
        d = -1; %顺时针旋转
    end
    % CORDIC算法是三个公式
    x(i+1) = x(i) - d*y(i)*(2^(-(i-1)));
    y(i+1) = y(i) + d*x(i)*(2^(-(i-1)));
    z(i+1) = z(i) - d*atan(2^(-(i-1)));
end
cosa = vpa(x(17),10)
sina = vpa(y(17),10)
c = vpa(z(17),10)

FPGA实现

旋转角度需要提前存在ROM中，另外还需要用到加法器和移位操作。根据输入： X Y Z 得到 输出：旋转后的 X’ 和 Y‘

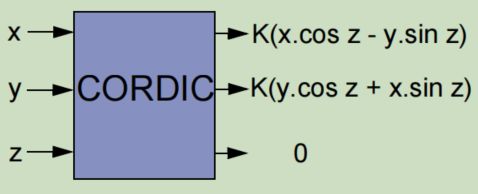
单次迭代的框图：

**旋转角度：**通过xy的最高有效位进行XOR异或操作，我们即可判断xy最高有效位的同号还是异号，从而判断出旋转角度 d 是 -1 还是 1 。
**选择信号：**根据公式，当X进行加法运算的时候，Y进行减法运算，或者X减法Y加法，因此二者的选择是互为相反，而选择信号均来自XOR结果，因此在Y的选择器处进行了取反操作，为保证与X互为相反的加减运算。（起到控制加减法的作用）
二选一多路器：根据选择信号来判断是进行加法还是减法操作。

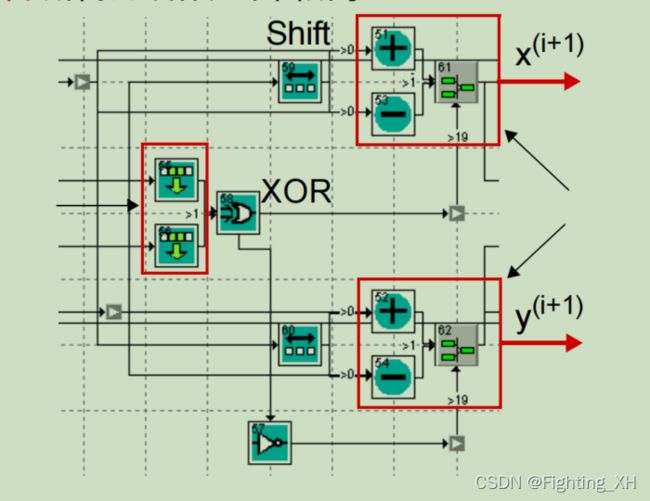
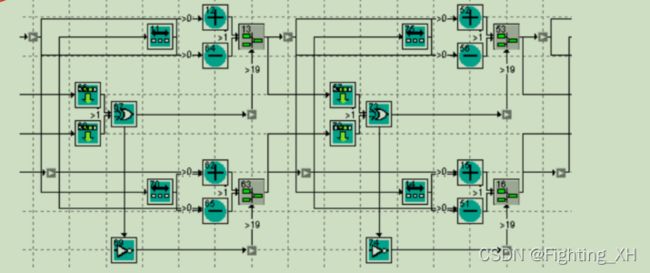
两次迭代框图：
两次迭代就是逻辑的复制。
本文的学习资料参考包含verilog代码及测试文件。该代码采用如下的数学矩阵来计算。
首先确定迭代次数以及增益K的数值，然后根据查找表的角度值即可实现。

CORDIC旋转模式的verilog代码

该代码中将迭代次数设置为16，以下是代码的学习理解：

//*********************************************************
//用该模块的时候需要给予一个角度angle
//已知角度θ，求正弦sinθ和余弦cosθ

//思想:若向量模值为1，则其x坐标就是余弦值，y坐标就是正弦值。
//利用这一点，从(K,0)处迭代旋转至θ处的单位矢量即可。

//*********************************************************


module cordic_A(
input 			clk,
input 			rst_n,
input	[8:0]	angle,
input			start,

output 	reg signed[31:0]	Sin,
output 	reg signed[31:0]	Cos,
output 			finished

);


parameter angle_0 = 32'd2949120;		//45度*2^16
parameter angle_1 = 32'd1740992;     //26.5651度*2^16
parameter angle_2 = 32'd919872;      //14.0362度*2^16
parameter angle_3 = 32'd466944;      //7.1250度*2^16
parameter angle_4 = 32'd234368;      //3.5763度*2^16
parameter angle_5 = 32'd117312;     //1.7899度*2^16
parameter angle_6 = 32'd58688;      //0.8952度*2^16
parameter angle_7 = 32'd29312;      //0.4476度*2^16
parameter angle_8 = 32'd14656;      //0.2238度*2^16
parameter angle_9 = 32'd7360;      //0.1119度*2^16
parameter angle_10 = 32'd3648;      //0.0560度*2^16
parameter angle_11 = 32'd1856;	    //0.0280度*2^16
parameter angle_12 = 32'd896;      //0.0140度*2^16
parameter angle_13 = 32'd448;      //0.0070度*2^16
parameter angle_14 = 32'd256;      //0.0035度*2^16
parameter angle_15 = 32'd128;      //0.0018度*2^16

parameter pipeline = 16;   //迭代次数
parameter K = 32'h09b74;			//0.607253*2^16,


// reg signed [31:0] Sin;
// reg signed [31:0] Cos;

reg signed 	[31:0] 		x0 =0,y0 =0,z0 =0;
reg signed 	[31:0] 		x1 =0,y1 =0,z1 =0;
reg signed 	[31:0] 		x2 =0,y2 =0,z2 =0;
reg signed 	[31:0] 		x3 =0,y3 =0,z3 =0;
reg signed 	[31:0] 		x4 =0,y4 =0,z4 =0;
reg signed 	[31:0] 		x5 =0,y5 =0,z5 =0;
reg signed 	[31:0] 		x6 =0,y6 =0,z6 =0;
reg signed 	[31:0] 		x7 =0,y7 =0,z7 =0;
reg signed 	[31:0] 		x8 =0,y8 =0,z8 =0;
reg signed 	[31:0] 		x9 =0,y9 =0,z9 =0;
reg signed 	[31:0] 		x10=0,y10=0,z10=0;
reg signed 	[31:0] 		x11=0,y11=0,z11=0;
reg signed 	[31:0] 		x12=0,y12=0,z12=0;
reg signed 	[31:0] 		x13=0,y13=0,z13=0;
reg signed 	[31:0] 		x14=0,y14=0,z14=0;
reg signed 	[31:0] 		x15=0,y15=0,z15=0;
reg signed 	[31:0] 		x16=0,y16=0,z16=0;

reg  [4:0]           count;

always@(posedge clk or negedge rst_n)begin
	if(!rst_n)
		count <= 'b0;
	else if(start)begin
		if(count != 5'd18)
			count <= count + 1'b1;
		else 
			count <= count;
	end
end

assign finished = (count == 5'd18)?1'b1:1'b0;

always@(posedge clk or negedge rst_n)begin
	if(!rst_n)begin
		x0 <= 'b0;
		y0 <= 'b0;
		z0 <= 'b0;

	end
	
	else begin
		x0 <= K;  //该模块种将原始的xy坐标采用了cordic简化后的形式，分别为K，0
		//当我们进行整幅图像的旋转的时候，可以连接图像的行列计数器（xy坐标）
		y0 <= 32'd0;
		z0 <= angle << 16;
	end
end 

always@(posedge clk or negedge rst_n)begin//第一次迭代
	if(!rst_n)begin
		x1 <= 'b0;
		y1 <= 'b0;
		z1 <= 'b0;
	end
	else if(z0[31]) begin  //由方向Z0的高位进行旋转方向判断，高位为真，说明总旋转角度θ为负，di = -1
		x1 <= x0 + y0;
		y1 <= y0 - x0;  //x1 和 y1 的加减运算总相反
		z1 <= z0 + angle_0;
	end
	else begin
		x1 <= x0 - y0;
		y1 <= y0 + x0;
		z1 <= z0 - angle_0;		
	end
end 

always@(posedge clk or negedge rst_n)begin//第二次迭代
	if(!rst_n)begin
		x2 <= 'b0;
		y2 <= 'b0;
		z2 <= 'b0;
	end
	else if(z1[31]) begin
		x2 <= x1 + (y1>>>1);  //有符号数所以采用>>>进行移位
		y2 <= y1 - (x1>>>1);
		z2 <= z1 + angle_1;
	end
	else begin
		x2 <= x1 - (y1>>>1);
		y2 <= y1 + (x1>>>1);
		z2 <= z1 - angle_1;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第3次迭代
	if(!rst_n)begin
		x3 <= 'b0;
		y3 <= 'b0;
		z3 <= 'b0;
	end
	else if(z2[31]) begin
		x3 <= x2 + (y2>>>2);
		y3 <= y2 - (x2>>>2);
		z3 <= z2 + angle_2;
	end
	else begin
		x3 <= x2 - (y2>>>2);
		y3 <= y2 + (x2>>>2);
		z3 <= z2 - angle_2;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第4次迭代
	if(!rst_n)begin
		x4 <= 'b0;
		y4 <= 'b0;
		z4 <= 'b0;
	end
	else if(z3[31]) begin
		x4 <= x3 + (y3>>>3);
		y4 <= y3 - (x3>>>3);
		z4 <= z3 + angle_3;
	end
	else begin
		x4 <= x3 - (y3>>>3);
		y4 <= y3 + (x3>>>3);
		z4 <= z3 - angle_3;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第5次迭代
	if(!rst_n)begin
		x5 <= 'b0;
		y5 <= 'b0;
		z5 <= 'b0;
	end
	else if(z4[31]) begin
		x5 <= x4 + (y4>>>4);
		y5 <= y4 - (x4>>>4);
		z5 <= z4 + angle_4;
	end
	else begin
		x5 <= x4 - (y4>>>4);
		y5 <= y4 + (x4>>>4);
		z5 <= z4 - angle_4;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第6次迭代
	if(!rst_n)begin
		x6 <= 'b0;
		y6 <= 'b0;
		z6 <= 'b0;
	end
	else if(z5[31]) begin
		x6 <= x5 + (y5>>>5);
		y6 <= y5 - (x5>>>5);
		z6 <= z5 + angle_5;
	end
	else begin
		x6 <= x5 - (y5>>>5);
		y6 <= y5 + (x5>>>5);
		z6 <= z5 - angle_5;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第7次迭代
	if(!rst_n)begin
		x7 <= 'b0;
		y7 <= 'b0;
		z7 <= 'b0;
	end
	else if(z6[31]) begin
		x7 <= x6 + (y6>>>6);
		y7 <= y6 - (x6>>>6);
		z7 <= z6 + angle_6;
	end
	else begin
		x7 <= x6 - (y6>>>6);
		y7 <= y6 + (x6>>>6);
		z7 <= z6 - angle_6;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第8次迭代
	if(!rst_n)begin
		x8 <= 'b0;
		y8 <= 'b0;
		z8 <= 'b0;
	end
	else if(z7[31]) begin
		x8 <= x7 + (y7>>>7);
		y8 <= y7 - (x7>>>7);
		z8 <= z7 + angle_7;
	end
	else begin
		x8 <= x7 - (y7>>>7);
		y8 <= y7 + (x7>>>7);
		z8 <= z7 - angle_7;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第9次迭代
	if(!rst_n)begin
		x9 <= 'b0;
		y9 <= 'b0;
		z9 <= 'b0;
	end
	else if(z8[31]) begin
		x9 <= x8 + (y8>>>8);
		y9 <= y8 - (x8>>>8);
		z9 <= z8 + angle_8;
	end
	else begin
		x9 <= x8 - (y8>>>8);
		y9 <= y8 + (x8>>>8);
		z9 <= z8 - angle_8;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第10次迭代
	if(!rst_n)begin
		x10 <= 'b0;
		y10 <= 'b0;
		z10 <= 'b0;
	end
	else if(z9[31]) begin
		x10 <= x9 + (y9>>>9);
		y10 <= y9 - (x9>>>9);
		z10 <= z9 + angle_9;
	end
	else begin
		x10 <= x9 - (y9>>>9);
		y10 <= y9 + (x9>>>9);
		z10 <= z9 - angle_9;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第11次迭代
	if(!rst_n)begin
		x11 <= 'b0;
		y11 <= 'b0;
		z11 <= 'b0;
	end
	else if(z10[31]) begin
		x11 <= x10 + (y10>>>10);
		y11 <= y10 - (x10>>>10);
		z11 <= z10 + angle_10;
	end
	else begin
		x11 <= x10 - (y10>>>10);
		y11 <= y10 + (x10>>>10);
		z11 <= z10 - angle_10;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第12次迭代
	if(!rst_n)begin
		x12 <= 'b0;
		y12 <= 'b0;
		z12 <= 'b0;
	end
	else if(z11[31]) begin
		x12 <= x11 + (y11>>>11);
		y12 <= y11 - (x11>>>11);
		z12 <= z11 + angle_11;
	end
	else begin
		x12 <= x11 - (y11>>>11);
		y12 <= y11 + (x11>>>11);
		z12 <= z11 - angle_11;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第13次迭代
	if(!rst_n)begin
		x13 <= 'b0;
		y13 <= 'b0;
		z13 <= 'b0;
	end
	else if(z12[31]) begin
		x13 <= x12 + (y12>>>12);
		y13 <= y12 - (x12>>>12);
		z13 <= z12 + angle_12;
	end
	else begin
		x13 <= x12 - (y12>>>12);
		y13 <= y12 + (x12>>>12);
		z13 <= z12 - angle_12;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第14次迭代
	if(!rst_n)begin
		x14 <= 'b0;
		y14 <= 'b0;
		z14 <= 'b0;
	end
	else if(z13[31]) begin
		x14 <= x13 + (y13>>>13);
		y14 <= y13 - (x13>>>13);
		z14 <= z13 + angle_13;
	end
	else begin
		x14 <= x13 - (y13>>>13);
		y14 <= y13 + (x13>>>13);
		z14 <= z13 - angle_13;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第15次迭代
	if(!rst_n)begin
		x15 <= 'b0;
		y15 <= 'b0;
		z15 <= 'b0;
	end
	else if(z14[31]) begin
		x15 <= x14 + (y14>>>14);
		y15 <= y14 - (x14>>>14);
		z15 <= z14 + angle_14;
	end
	else begin
		x15 <= x14 - (y14>>>14);
		y15 <= y14 + (x14>>>14);
		z15 <= z14 - angle_14;	
	end
end 

always@(posedge clk or negedge rst_n)begin//第16次迭代
	if(!rst_n)begin
		x16 <= 'b0;
		y16 <= 'b0;
		z16 <= 'b0;
	end
	else if(z15[31]) begin
		x16 <= x15 + (y15>>>15);
		y16 <= y15 - (x15>>>15);
		z16 <= z15 + angle_15;
	end
	else begin
		x16 <= x15 - (y15>>>15);
		y16 <= y15 + (x15>>>15);
		z16 <= z15 - angle_15;	
	end
end 

always@(posedge clk or negedge rst_n)begin
	if(!rst_n)begin
		 Cos <= 'b0;
		 Sin <= 'b0;
	end
	else begin
        Sin <= y16;   
        Cos <= x16;   //得到最终的正弦余弦值，即可根据原始坐标，得到旋转后的坐标。
	end
end 

endmodule

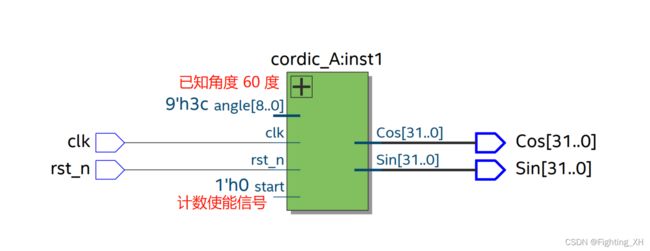
对CORDIC算法进行封装，同时给与一个旋转角度60度。

module top(

				input clk,
				input rst_n,

				output 	 signed [31:0]	Sin,
				output 	 signed [31:0]	Cos

);

cordic_A inst1(
		.clk(clk),
		.rst_n(rst_n),
		.angle(60),
		.start(start),
		
		.Sin(Sin),
		.Cos(Cos),
		.finished(finished)
		
);
endmodule

RTL图

得到如下的RTL图：

可以看到给与60度旋转角，根据旋转角，采用CORDIC算法即可得到最终的正余弦值。

对CORDIC算法tb仿真（不采用top文件，用cordic_A）

`timescale 1ns/1ns

module cordic_Atb();

parameter PERIOD = 10;
reg clk;
reg rst_n;
reg [8:0]angle;
reg start;

wire 	 [31:0] 		Sin;
wire 	 [31:0] 		Cos;
wire 					finished;
integer i;

initial begin
	clk = 0;
	rst_n = 0;
	start = 0;
	angle = 'b0;

	#10 rst_n =1;
			
	#10 start = 1'b1;
   #10000000  $stop;	
end

initial
begin
    #0 angle = 9'd20;
   for(i=0;i<10000;i=i+1)
	begin
		#400;
		angle <= angle + 9'd20;
	end
end		
	

always #(PERIOD/2) clk = ~clk;

cordic_A inst1(
		.clk(clk),
		.rst_n(rst_n),
		.angle(angle),
		.start(start),
		
		.Sin(Sin),
		.Cos(Cos),
		.finished(finished)
		
);

endmodule

向量模式

向量模式相当于旋转模式的倒推，是将给定的向量旋转到X轴上，因此我们就有了旋转后的坐标，根据旋转后的坐标（梯度模值），可确定处旋转的角度（梯度方向）。

寄存器X值为梯度模值，符号判决因子d与寄存器y的值相反，得到d后，仍然使用旋转模式中推到的角度累加器Z来计算梯度方向。