C++下OpenCV学习笔记----离散傅里叶变换

C++下OpenCV学习笔记

----离散傅里叶变换

一.离散傅里叶变换

1. 原理
   对一张图像使用傅立叶变换就是将它分解成正弦和余弦两部分。也就是将图像从空间域(spatial domain)转换到频域(frequency domain)。

在频域中，对于一幅图像，高频部分代表了图像的细节、纹理信息；低频部分代表了图像的轮廓信息。

2. 理论基础
   任一函数都可以表示成无数个正弦和余弦函数的和的形式。傅立叶变换就是一个用来将函数分解的工具。
3. 数学公式 :二维

f是空间域(spatial domain)值
F是频域(frequency domain)值
转换之后的频域值是复数

• 显示傅立叶变换之后的结果需要使用实数图像(real image) 加虚数图像(complex image), 或者幅度图像(magitude image)加相位图像(phase image)。
• 在实际的图像处理过程中，仅仅使用了幅度图像，因为幅度图像包含了原图像的几乎所有我们需要的几何信息。
• 若想通过修改幅度图像或者相位图像的方法来间接修改原空间图像，则需要使用逆傅立叶变换得到修改后的空间图像，必须同时保留幅度图像和相位图像。

4. 应用
   在图像处理中：图像增强与图像去噪，图像分割之边缘检测，图像特征提取，图像压缩等。

二.dft( )函数

1. 作用
   对一维或二维浮点数数组进行正向或反向的离散傅里叶变换。
2. 原型
   void dft(InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0);

第一个参数：表示输入的矩阵，可为实数或者虚数。
第二个参数：表示输出的矩阵。
第三个参数：表示转换的标识符。决定输出矩阵的尺寸和类型。默认为0.
第四个参数：默认为0。当此参数设为非零时，函数会假设只有输入矩阵的第一个非零行包含非零元素，或只有输出矩阵的一个非零行包含非零元素。

名称	意义
DFT_INVERSE	用一维或二维逆变换代替默认的正向变换
DFT_SCALE	缩放比例标识符，输出的结果都会以1/N进行缩放，通常与DFT_INVERSE一起使用
DFT_ROWS	对输入矩阵的每行进行正向或反向的变换，此标识符可以在处理多种矢量的时候用于减小资源开销，这些处理常是三维或高维变换等复杂操作
DFT_COMPLEX_OUTPUT	进行一维或二维实数数组正变换。这样的结果虽然是复数阵列，但拥有复数的共轭对称性（CCS），所以可以被写成一个拥有同样尺寸的实数阵列
DFT_REAL_OUTPUT	进行一维或二维复数数组反变换。这样的结果通常是一个大小相同的复矩阵。如果输入的矩阵有复数的共轭对称性（比如是一个带有DFT_COMPLEX_OUTPUT标识符的正变换结果），则会输出实矩阵

三.返回DFT最优尺寸大小：getOptimalDFTSize( )函数

1. 作用：
   用于计算扩充多少的图像来提高离散傅里叶变换的速度。
2. 原型
   int getOptimalDFTSize(int vecsize);

第一个参数：表示图片的rows and cols.

四.扩充图像边界：copyMakeBorder( )函数

void copyMakeBorder(InputArray src, OutputArray dst, int top, int bottom, int left, int right, int borderType, const Scalar& value=Scalar());

第一个参数：表示源图像
第二个参数：表示输出结果，需要与源图像有一样的尺寸和类型，且size应为Size(src.cols+left+right, src.rows+top+bottom)
第三/四/五/六个参数：表示在源图像的四个方向上扩充多少像素
第七个参数：表示边界类型。常见取值为BORDER_CONSTANT，可参考borderInterpolate( )
第八个参数：默认为0。若borderType取值为BORDER_CONSTANT时，表示为边界值

• 当图像的尺寸是2，3，5的整数倍时，计算速度最快。

五.计算二维矢量的幅值：magnitude( )函数

1. 原理
2. 原型
   void magnitude(InputArray x, InputArray y, OutputArray magnitude);

第一个参数：表示矢量的浮点型x坐标值，也就是实部
第二个参数：表示矢量的浮点型y坐标值，也就是虚部
第三个参数：表示输出的幅值。和x有同样的尺寸和类型

六.计算自然对数：log( )函数

1. 原理
2. 原型
   void log(InputArray src,OutputArray dst);

第一个参数：表示输入图像
第二个参数：表示得到的对数值

七.矩阵归一化：normalize( )函数

void normalize(InputArray src,OutputArray dst, double alpha = 1, double beta = 0, int norm_type = NORM_L2, int dtype = -1, InputArray mask = noArray());

第一个参数：表示源图像
第二个参数：表示输出图像。和源图像有同样 的尺寸和类型
第三/四个参数：表示归一化的最大值和最小值。默认为1和0
第五个参数：表示归一化的类型。默认为NORM_L2
NORM_MINMAX： 数组的数值被平移或缩放到一个指定的范围，线性归一化，一般较常用。
NORM_INF：归一化数组的C-范数（绝对值的最大值）
NORM_L1：归一化数组的L1-范数（绝对值的和）
NORM_L2：归一化数组的L2-范数（欧几里得）
第六个参数：默认为-1。当参数取值为负时，输出矩阵和输入矩阵有同样的尺寸和类型；否则，输出矩阵和输入矩阵只是通道数相同，且此时图像的深度为CV_MAT_DEPTH(dtype).
第七个参数：表示可选的操作掩膜。默认为noArray()

八.代码实现

#include 
#include 

using namespace std;
using namespace cv;

int main()
{
    Mat srcImage = imread("C://Users//441//Desktop//ZL//夏目//1.jpg", IMREAD_GRAYSCALE);       
    if (srcImage.empty())
    {
        cout << "读取图片错误!" << endl;
        return -1;
    }
    imshow("原始灰度图", srcImage);

    Mat padded;                 
    int m = getOptimalDFTSize(srcImage.rows);
    int n = getOptimalDFTSize(srcImage.cols);
    //填充输入图像srcImage
    copyMakeBorder(srcImage, padded, 0, m - srcImage.rows, 0, n - srcImage.cols, BORDER_CONSTANT, Scalar::all(0));

    Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(),CV_32F) };
    Mat complexI;
    merge(planes, 2, complexI);     //分配储存空间并融合

    dft(complexI, complexI);        //离散傅里叶变换

    //计算幅值
    split(complexI, planes);      
    magnitude(planes[0], planes[1], planes[0]);   
    Mat magImage = planes[0];

    magImage += Scalar::all(1);
    log(magImage, magImage);          //转换到对数尺度

    //奇数行/列：频谱裁剪
    magImage = magImage(Rect(0, 0, magImage.cols & -2, magImage.rows & -2));
    //重排象限
    int cx = magImage.cols / 2;
    int cy = magImage.rows / 2;
    //子图像
    Mat q0(magImage, Rect(0, 0, cx, cy));       //左上角
    Mat q1(magImage, Rect(cx, 0, cx, cy));      //右上角
    Mat q2(magImage, Rect(0, cy, cx, cy));      //左下角
    Mat q3(magImage, Rect(cx, cy, cx, cy));     //右下角
    //变换左上角和右下角象限
    Mat tmp;
    q0.copyTo(tmp);
    q3.copyTo(q0);
    tmp.copyTo(q3);
    //变换右上角和左下角象限
    q1.copyTo(tmp);
    q2.copyTo(q1);
    tmp.copyTo(q2);

    //归一化处理
    normalize(magImage, magImage, 0, 1, CV_MINMAX);

    imshow("频谱图", magImage);
    waitKey(0);
    return 0;
}

九.运行结果

十.代码分析

1. 载入原始灰度图像

Mat srcImage = imread("C://Users//441//Desktop//ZL//夏目//1.jpg", IMREAD_GRAYSCALE);       
if (srcImage.empty())
{
    cout << "读取图片错误!" << endl;
    return -1;
}
imshow("原始灰度图", srcImage);

2. 将图像扩大到合适尺寸
   上方和左方不做填充处理.

Mat padded;                
int m = getOptimalDFTSize(srcImage.rows);
int n = getOptimalDFTSize(srcImage.cols);
copyMakeBorder(srcImage, padded, 0, m - srcImage.rows, 0, n - srcImage.cols, BORDER_CONSTANT, Scalar::all(0));

3. 为傅里叶变换的结果（实部和虚部）分配储存空间
   并将planes融合合并成一个多通道数组complexI.

Mat planes[] = { Mat_<float>(padded), Mat::zeros(padded.size(),CV_32F) };
Mat complexI;
merge(planes, 2, complexI); 

4. 进行离散傅里叶变换
   输入输出为同一图像.

dft(complexI, complexI); 

5. 将复数转化为幅值
   复数包含实数部分（Re）和虚数部分（Im），离散傅里叶变换的复数结果的幅度可表示为：
   

• 计算幅值，转换到对数尺度(logarithmic scale) => log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
• 将多通道数组complexI分离成几个单通道数组planes => planes[0] = Re(DFT(I),planes[1] = Im(DFT(I))
• planes[0]为实部，planes[1]为虚部

split(complexI, planes);        
magnitude(planes[0], planes[1], planes[0]);    
Mat magImage = planes[0];

6. 进行对数尺度(logarithmic scale)缩放
   傅里叶变换的幅度值高值在屏幕上显示为白点，低值在屏幕上显示为黑点，且高低值变化无法有效分辨。为了在屏幕上凸显出高低变化的连续性，采用对数尺寸代替线性尺寸。公式为：
   

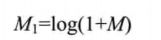
magImage += Scalar::all(1);
log(magImage, magImage);  

7. 剪切和重分布幅度图象限

• 在第二步中延扩了图像，需将新添加的像素剔除
• 在第五步中重新分布幅度图象限位置：从中间划开，得到四张1/4子图像，将每张子图像看成幅度图的一个象限，重新分布，即将四个角点重叠到图片中心

//奇数行/列：频谱裁剪
magImage = magImage(Rect(0, 0, magImage.cols & -2, magImage.rows & -2));
//重排象限
int cx = magImage.cols / 2;
int cy = magImage.rows / 2;
//子图像
Mat q0(magImage, Rect(0, 0, cx, cy));       //左上角
Mat q1(magImage, Rect(cx, 0, cx, cy));      //右上角
Mat q2(magImage, Rect(0, cy, cx, cy));      //左下角
Mat q3(magImage, Rect(cx, cy, cx, cy));     //右下角
//变换左上角和右下角象限
Mat tmp;
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3);
//变换右上角和左下角象限
q1.copyTo(tmp);
q2.copyTo(q1);
tmp.copyTo(q2);

8. 归一化处理
   重分布的图像幅度值仍超过可显示范围[0, 1]，将幅度归一化到可显示的范围。

normalize(magImage, magImage, 0, 1, CV_MINMAX);

9. 显示效果图

imshow("频谱图", magImage);
waitKey(0);
return 0;