深度学习-李宏毅GAN学习之理论原理

目的

通过学习和理解李宏毅的GAN课程，对GAN有更加深入的理解，希望能结合李宏毅老师的课件和自己的理解把GAN的理论基础搞明白，这样就可以去学习更多GAN的变种，同时也可以帮助更多想入门GAN的朋友一点点经验吧。

GAN的理论原理

通俗的讲，GAN中文叫做生成对抗网络，就是双方互相博弈（生成器和鉴别器，鉴别器要最大化，求出分布差异，生成器要最小化，降低差异），最后达到一种平衡状态。我们用GAN做图片生成，做风格学习，做语音识别或者做语音和声纹分离，本质上都是在做概率分布的学习，我们希望我们的模型可以去接近真实分布。

简单的说，就是我希望训练一个模型，模型用来学习真实样本的分布，很多时候我们是不知道真实样本的分布的，但是它确实是存在的。那我们要怎么来学习这个分布呢，最常见的就是用极大似然估计，即我们希望我们的模型生成的样本，看起来很最像是真实的分布生成的样本。换句话说，我们希望模型的样本分布和真实样本分布差距越来越小，因此引入了散度的概念，即两个分布之间的差异，不是距离，应该是信息损耗。这个属于信息论里的概念，有兴趣的可以去了解下[这篇文章]，了解下信息量，信息熵，相对熵（KL散度），更好的理解GAN。

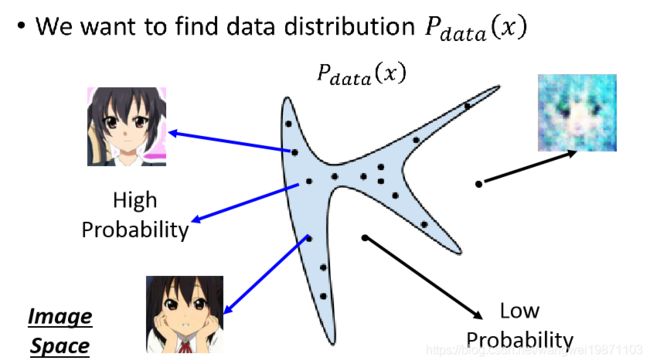
举个生成图片的例子来解释下GAN在做什么。
假设上面中间那个很奇怪的图形是我们真实数据的分布Pdata，简化成二维的这么个图形，上面的每一个点就是一张图片，可以看到左边从图形里面采样到的样本点是很不错，右边从图形外面采样的就比较差了。那我们要做的当然就是去找到这个Pdata啦，希望可以用上面公式来表达。我们是通过很多张样本分析，能知道哪些地方的样本是比较好的，即知道哪里地方出现的好的样本概率高，也知道哪些地方出现差的样本概率高。

极大似然估计

那我们有什么方法通过样本来找出真实数据的分布呢，用的就是极大似然估计，其实也就是估计下，并非帧的能找到，只是极大可能的接近真实分布。

1.我们有参数θ的分布PG
2.我们想调整参数θ，使得Pdata和PG越接近越好
3.从真实数据分布Pdata中采样一堆数据x1,x2…，调整参数θ，使得x1,x2…从PG产生的概率越大越好
4.因此就有了关于θ的似然函数

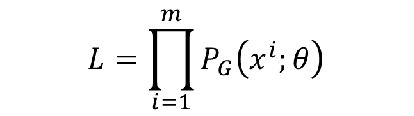
整体的概率就是每个样本从PG里产生的最大概率的乘积。

我们想让这个L最大，即我们需要找到参数θ，使得L最大，即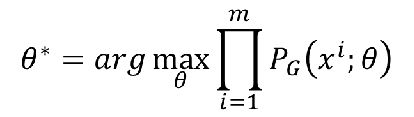
一般累乘比较难计算，我们用取log化为累加



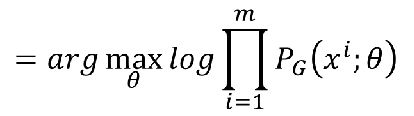
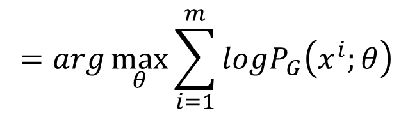
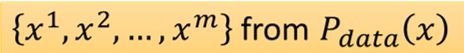
因为样本都是取自Pdata，而且求和，我们可以近似转换为期望

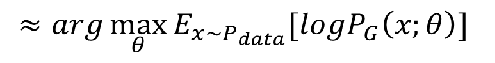
期望对连续随机变量也可以转换为积分问题

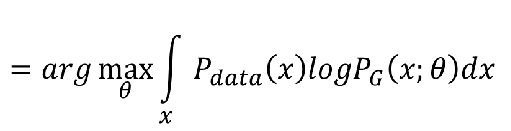
然后为了凑出散度公式，再后面加上了一项

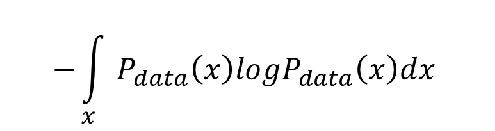
即如下

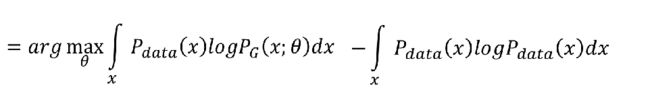
KL散度的公式，可以参考

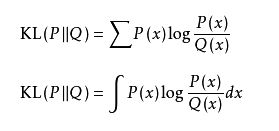
由于编辑公式太麻烦，决定手写补上中间的过程，便于理解，字难看了点，能明白过程就行。

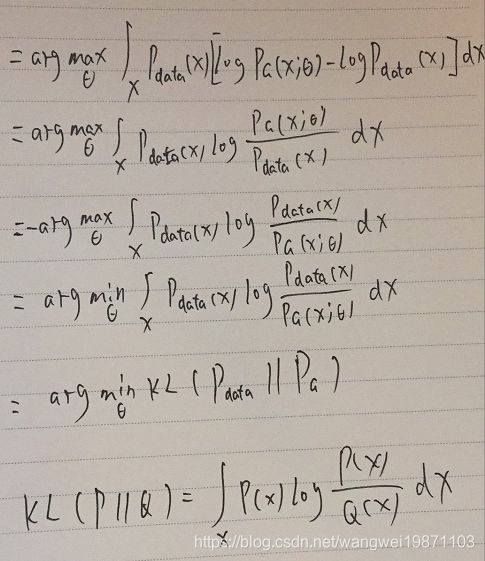
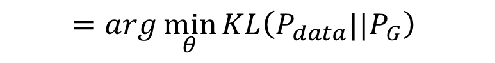
可以看到，极大似然估计可以变换成KL散度，即两个分布的差异。
我们现在的目标变成求θ，使得两个分部之间差异最小。

生成器G

那现在问题来了，PG怎么来呢，传统的方法是用高斯混合模型的组合而来的，貌似是用很多高斯分部曲线的组合来拟合真实分布，但是貌似对图片效果不好，模糊，所以我们就尝试用神经网络来生成，反正只要能找到一组参数θ，生成PG就行，神经网络刚好擅长这个啊。

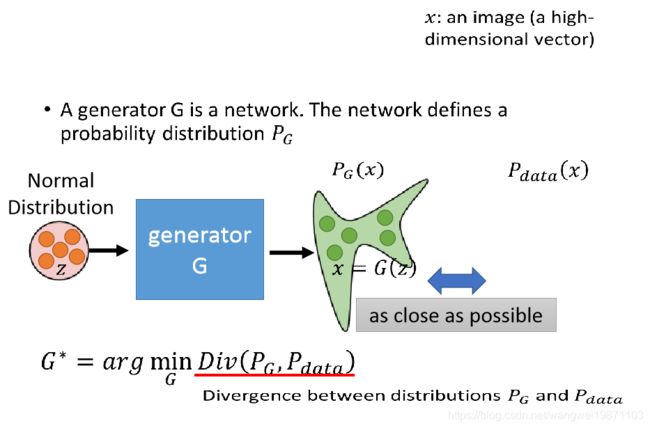
我们可以定义一个噪音分布用于采样，可以是高斯分部，也可以是均匀分布，中间是神经网络，输入样本Z，无论前面是高斯还是均匀分布，都可以被G学习后变为后面的PG分布，我们希望分布PG和真实的分布Pdata越接近越好。所以问题变成我们要找一个G，生成一个分布PG，使得PG和Pdata越接近越好，可以定义成：

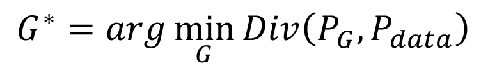
Div就是两个分布之间的散度(差异)，可以是KL散度，也可以是其他的比如JS散度。
简单就是说，为什么的目标等价于要找到一个神经网络G，生成的PG让两个分布之间的差距最小。（有没有发现GAN的核心一直围绕着2个分布之间的差异展开，其他很多的东西都是为这个思想服务，不论前面的最大似然估计，还是后面要讲的交叉熵损失函数都是这个原理）

判别器D

但是问题由来了，我们不知道PG和Pdata是什么，怎么来衡量他们的差异呢。我们可以采样啊，我们可以通过G去生成样本，就是PG中采样来的，同样，我们也有真实样本，从Pdata采样来的。然后用伸进网络当一个判别器D来解决Div，来判断这些样本的差异情况。

假设我们采样的样本如下，我们把所有样本给D，训练D为一个二分类器，如果Div大，就给PG低分数，给Pdata高分数，如果Div小，就给这2个差不多分数，直到Div=0时，两个分数就一样了，都为0.5，也说明无法判断样本是哪个分布来的，理论上即达到PG和Pdata一样了。

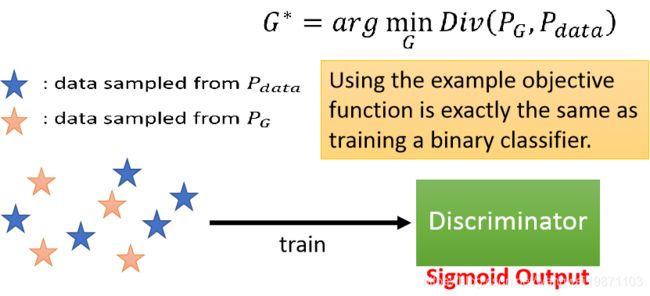
我们固定G，训练D，接下来要为D选择目标函数V(G,D)啦，我们希望来自Pdata的越大越好，来自PG的越小越好，即我们希望整体V(G,D)越大越好

即我们需要训练个D，使得V(G,D)越大越好

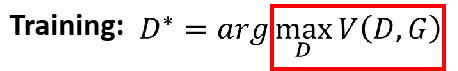
接下来讲下为什么D和Div相关

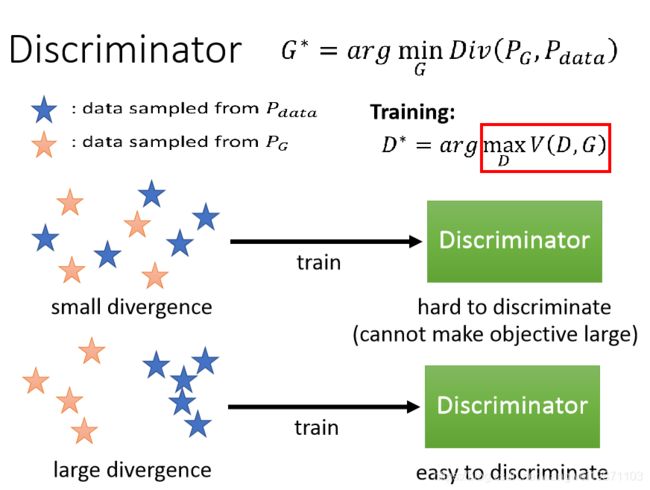
可以看到，如果Div很小，则D就很难鉴别，如果Div很大，D就很容易鉴别，即D和Div是相关的。

我们将刚才的V的期望转换为积分

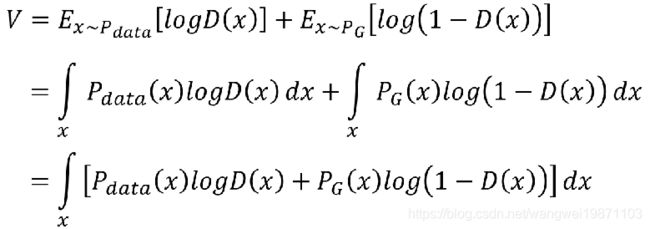
即我们需要求这个的最大值，假设 D(x)可以是任意函数，求积分最大，也就是求被积函数最大。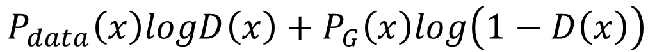
如下假设，可得V最大时候的D取值，就是函数求倒数，等于0，求出D

之后我们为了凑JS散度做了相应变换，以下为JS散度和KL散度的关系。

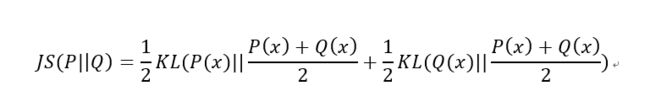
将D的值代入V(G,D)中，凑出JS散度，基本每步都有了，就不手动推导了


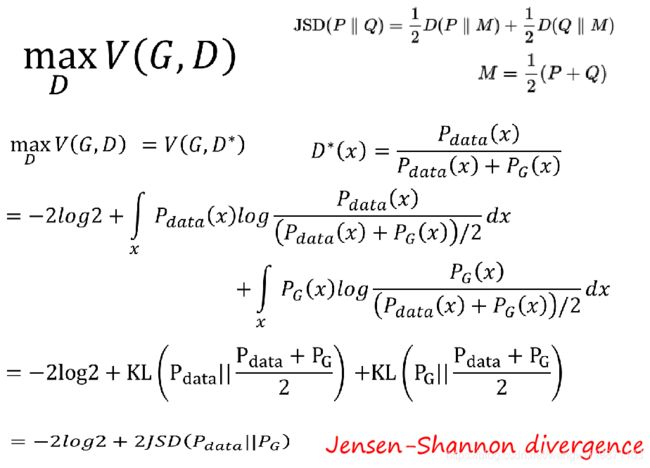
JS散度和KL散度可以认为是等效的，进过上面的推导，我们得出Div和V(G,D)的关系，最大V(G,D)，等价于Div

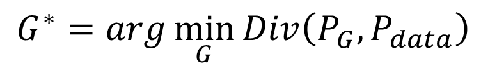
可以换为

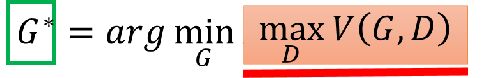
那现在我们来可视化看一下最大的V(G,D)和Div具体的关系：

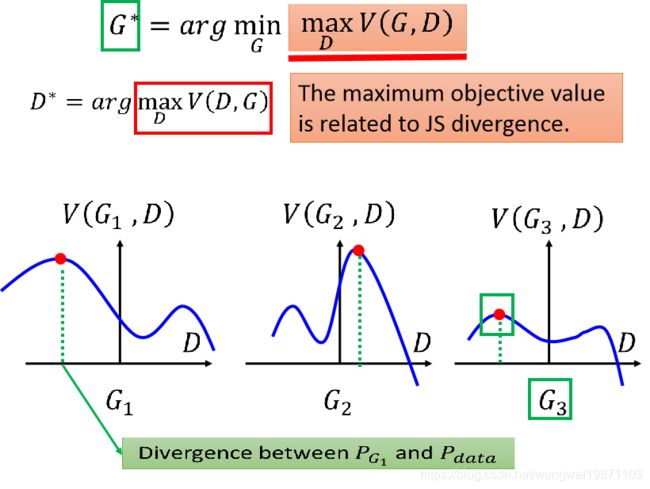
假设我们有三个G，可以看到在每个G中，根据上面的的公式，先找到了V(G,D)的最大值和相应的D，因为V(G,D)的最大值，就是散度，可以看到绿色的虚线就是散度的大小，然后我们又需要找到一个最小散度的G，可见G3的散度的是最小的，因此G3就是我们要找的分布差距最小的生成器。

具体求法

在说说上面的公式怎么求吧，G不变，先求出优化的D，然后再求出G，再求出优化的D，再求G，这样无限循环。

因此在求G的时候，D是不变得，所以可以简化为

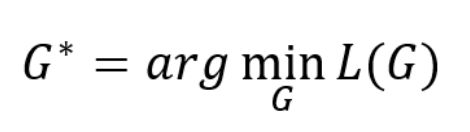
然后可以用梯度下降法优化G

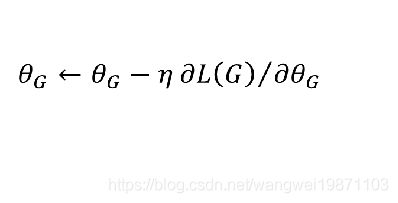
在求梯度的时候会涉及

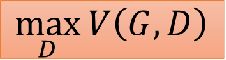
这个函数的求导，其实这个是可以求导的，

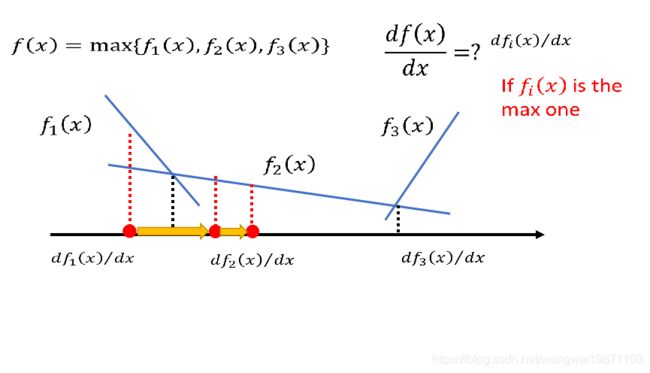
上图就是个max的函数，求导时，就是分段求导，x范围内哪个函数大，就用哪个来求导。

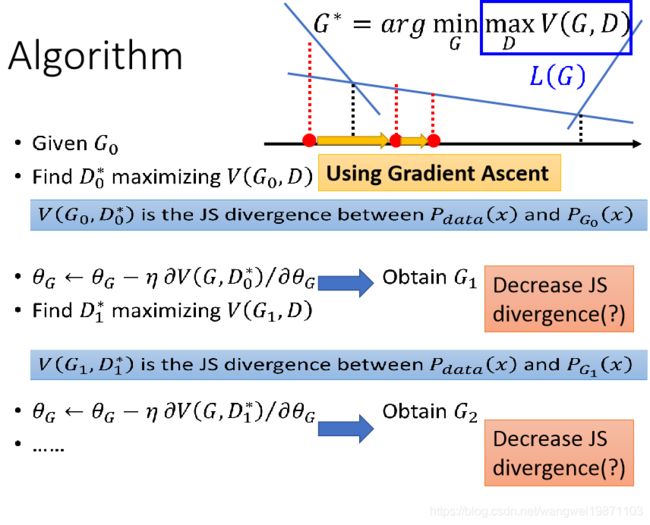
上图为整体算法，我们先生成G0，然后用梯度上升法最大化V(G0,D)，和求出相应的D1，然后用梯度下降法最小化V(G,D1)，即最小化散度，求出G1，然后继续上面的循环，直到最小化散度为0时候的Gx应该就是最好的生成器啦。

事实上我们的V(G,D)是换成均值来做的，D就是个二分类器，首先我们训练D，此时G是固定的，我们用梯度上升法训练K次，最大化V(G,D)，求出相应的D，然后固定D，用梯度下降法，最小化V(G,D)，此时只要求V(G,D)的后半段微分即可，前半段固定了，更新G，这样不断循环，最终使得V(G,D)最大化为0，即分布无差异。

好了，今天就到这里了，希望对学习理解有帮助，大神看见勿喷，仅为自己的学习理解，能力有限，请多包涵，图片来自李宏毅课件，侵删。