2022 第十三届蓝桥杯大赛软件赛省赛_PB python 大学 B 组 除了EFJ的题和解析

一共写了95分的题，和大家分享一下，没写EF勾，白给了55分，可惜

试题 A: 排列字母

感觉没啥好说的，就是签到

s = list(input())
s.sort()
print(''.join(s))

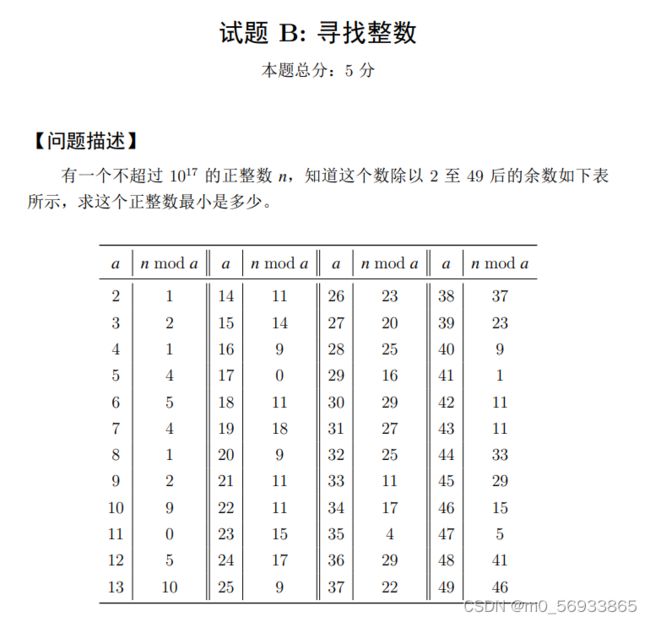
试题 B: 寻找整数

就是再签一次，怎么说呢，就是把0到pow（10，17）依次检查，查到满足条件就break，反正就挂后台等着就行了。

modNum = []
for i in range(2,13):
    modNum_i = input().split()
    modNum.append([modNum_i[0], modNum_i[1]])
    modNum.append([modNum_i[2], modNum_i[3]])
    modNum.append([modNum_i[4], modNum_i[5]])
    modNum.append([modNum_i[6], modNum_i[7]])
# print(modNum)
for i in range(1, pow(10,17)):
    iIsFind = False
    for j in range(len(modNum)):
        if i % int(modNum[j][0]) != int(modNum[j][1]):
            break
        if j == len(modNum) - 1:
            iIsFind = True
    if iIsFind:
        print(i)
        exit()

input:就是复制下题里的表格，然后等

2 1 14 11 26 23 38 37
3 2 15 14 27 20 39 23
4 1 16 9 28 25 40 9
5 4 17 0 29 16 41 1
6 5 18 11 30 29 42 11
7 4 19 18 31 27 43 11
8 1 20 9 32 25 44 33
9 2 21 11 33 11 45 29
10 9 22 11 34 17 46 15
11 0 23 15 35 4 47 5
12 5 24 17 36 29 48 41
13 10 25 9 37 22 49 46

试题 C: 纸张尺寸

 可能就是动一下小脑瓜

A = {'A0' : [841, 1189], 'A1' : [594, 841], 'A2' : [420, 594], 'A3' : [297, 420],
     'A4' : [210, 297], 'A5' : [148, 210], 'A6' : [105, 148], 'A7' : [74, 105]}
sA = input()
print(A[sA][1])
print(A[sA][0])

试题 D: 数位排序

 

 这题打算用一个list存放【num,num_sum】全用int，内存是2*sizeofint*nMax=8Mb

可能我觉得写的好的地方就是用了cache，比如说计算25568的位数和，就先在cache找5568的位数和在加2。这样时间复杂度小，过的概率高一点。

感兴趣的话呃呃，可以亲自试一下，我当时是赌命的，调用10000次cache和进行10000次类型转变再求和，是调cache更占优势

list0 = [i for i in range(100000)]
print (datetime.utcnow().strftime('%Y-%m-%d %H:%M:%S.%f')[:-3])
for i in range(10000):
    a = list0[20056]
print (datetime.utcnow().strftime('%Y-%m-%d %H:%M:%S.%f')[:-3])

for i in range(10000):
    l = list(str(20056))
    a = int(l[0]) +int(l[1]) +int(l[2]) +int(l[3]) +int(l[4])
print (datetime.utcnow().strftime('%Y-%m-%d %H:%M:%S.%f')[:-3])

代码比较长凑合看吧

n = int(input()) + 1
m = input()
cache = [[i, i] for i in range(0,10)] # 注意，加入了[0]
# print(cache)
# 两位数
if n > 9:
    if n > 99:
        for i in range(10, 100):
            sum_i_ten = int(i/10)
            sum_i = sum_i_ten + cache[i % 10][0]
            cache.append([sum_i, i])
    else:
        for i in range(10, n):
            sum_i_ten = int(i/10)
            sum_i = sum_i_ten + cache[i % 10][0]
            cache.append([sum_i, i])

if(n > 99): # 三位数
    if (n > 999):  # 4位数
        for i in range(100, 1000):
            sum_i_ten = int(i/100)
            sum_i = sum_i_ten + cache[i % 100][0]
            cache.append([sum_i, i])
    else:
        for i in range(100, n):
            sum_i_ten = int(i/100)
            sum_i = sum_i_ten + cache[i % 100][0]
            cache.append([sum_i, i])

if(n > 999): # 4位数
    if (n > 9999):  # 5位数
        for i in range(1000, 10000):
            sum_i_ten = int(i/1000)
            sum_i = sum_i_ten + cache[i % 1000][0]
            cache.append([sum_i, i])
    else:
        for i in range(1000, n):
            sum_i_ten = int(i/1000)
            sum_i = sum_i_ten + cache[i % 1000][0]
            cache.append([sum_i, i])


if(n > 9999): # 5位数
    if (n > 99999):  # 6位数
        for i in range(10000, 100000):
            sum_i_ten = int(i/10000)
            sum_i = sum_i_ten + cache[i % 10000][0]
            cache.append([sum_i, i])
    else:
        for i in range(10000, n):
            sum_i_ten = int(i/10000)
            sum_i = sum_i_ten + cache[i % 10000][0]
            cache.append([sum_i, i])


if(n > 99999): # 6位数
    if (n > 999999):  # 7位数
        for i in range(100000, 1000000):
            sum_i_ten = int(i/100000)
            sum_i = sum_i_ten + cache[i % 100000][0]
            cache.append([sum_i, i])
    else:
        for i in range(100000, n):
            sum_i_ten = int(i/100000)
            sum_i = sum_i_ten + cache[i % 100000][0]
            cache.append([sum_i, i])
# if n == 1000000:

cache.sort()
print(cache[int(m)][1])

EF没写，感觉没时间了，直接rush硬菜了

试题 G: 全排列的价值

先简单介绍下数的价值，将n个数字随机排列后，数字m的前面有k个比m小的数字，k就是m的分数。题里说的挺明白的，，

简单介绍下思路，比如说有n个数字，进行全排列，有n！种排法，此时设n的所有排列价值为an。

向其中插入n+1，由于n+1大于其他数字，这个插入不会对其他数字的价值产生影响，但是会翻n+1倍。

比如n=2,12中插入3，会产生三个结果312、132、123。这个插入使得an的总价值翻了n+1倍，也就是an*（n+1）

向n个数字的排列中插入一个数字，有n+1种插法。这些插法中，由于n+1大于其他数字，n+1前有几个数字，n+1的价值就是几。分别为0,1,2...n。这些价值并不受排列的影响。在n！个排列中都可以这样插入，产生（0+1+2.。。+n）的价值。就是（0+1+2...+n）*n！。

a(n+1) = an*（n+1）+ （0+1+2...+n）*n！

然后就是代码：

可能写的有点混乱，因为昨晚猫在疯狂的叫。

第一次写的时候之间肌肉记忆for i in a， n，j in i+1，n：swap；dfs；swap

发现第二个用例都超市，然后就打算dp，突然想到了

n = int(input())
ansOfNum = 2
ans = 1
# a2 = 1
# a3 = a2 * 3 + (1+2)*2! = 9
# a4 = a3 * 4 + (1+2+3)*3! = 72
for i in range(ansOfNum, n ):
    Plus = 0
    for i in range(1, ansOfNum+1):
        Plus = (Plus + i) % 998244353
    culi = 1
    for i in range(1, ansOfNum+1):
        culi = (culi*i)  % 998244353
    ans = (ans*(ansOfNum+1) + (Plus * culi))  % 998244353
    ansOfNum = ansOfNum + 1
print(ans)

试题 H: 技能升级

对于 60% 的评测用例，1 ≤ N ≤ 104 , 1 ≤ M ≤ 107；

对于所有评测用例，1 ≤ N ≤ 105，1 ≤ M ≤ 2 × 109，1 ≤ Ai , Bi ≤ 106。 

这个就是每次找一个最大的Ai，然后用Bi修改Ai，别改成负的就行。

简单分析一下难点，对所有用例，AiBi全用int就够，10的5次方肯定不会超。

然后看看时间复杂度，每次找最大的Ai都要排序。考试的时候感觉这个应该是时间比较长，刚上网查了一下介于n log n和n之间，但是由于我们的list除了刚刚用过的Ai，其他的都是有序的，我们可以之间for循环遍历一次，pop出来，找到地方插入即可，时间复杂度介于0到n。这样就有可能不会被超市。

上代码

[n, m] = input().split()
[n, m] = [int(n), int(m)]
AB = []
att = 0
for i in range(n):
    ABi_str = input().split()
    AB.append([int(ABi_str[0]), int(ABi_str[1])])

AB.sort(reverse=True)
for i in range(m):

    # AB.sort(reverse=True)
    att = att + AB[0][0]
    if AB[0][0] - AB[0][1] < 0:
        AB[0][0] = 0
    else:
        AB[0][0] = AB[0][0] - AB[0][1]
    ABi = AB[0].copy()
    AB.pop(0)
    for j in range(1, n - 1):
        if AB[j][0] 
  
试题 I: 最长不下降子序列
 
  
 
  
 很经典的dp，是个考试原题改编，怎么说呢这种心情，补考 的时候老师把上次考试原卷拿来了。用我们班主任的话说，呃呃，我不好说了。
 
  
 
  
 思路就是，先求最长子序列看看吧。
 
  
从dp矩阵倒着读，如果某个数字后面都是比他小的，那么dp【i】就=1。
 
  
如果这个数字可以和后面的数字组成最长不下降子序列，那么dp【i】=最大的最长不下降子序列+1
 
  
dp中的最大值即为所求，我当时居然忘了最大值，不想写了、之间贴代码了。
 
  
 算了，简单说一嘴，定义dp连续k个数字的变化幅度：变化量/k，就是斜率，本次修改可以使这个幅度变为1，找个最小的就行了。
 
  
[n,k] = input().split()
[n, k] = [int(n), int(k)]
num = input().split()
# 先写求最长不下降子序列方法，

dpi = [0 for i in range(pow(10, 4) + 10)]
def findNumjMax(dpi:list, j):
    Maxofj = 0
    for i in range(j+1, n):
        if num[i] >= num[j]:
            # print(len(dpi))
            if dpi[i] >= Maxofj:
                Maxofj = dpi[i]+1
    return max(Maxofj,1)
def maxNotDeline(dpi):
    dpi[n-1] = 1

    for i in range(n,-1,-1):
        # print(i)
        dpi[i] = findNumjMax(dpi ,i)
maxNotDeline(dpi)

# 从num的n试到N - k位
min_k = k + 1 #最小坡度
for i in range(n-k+1):
    if dpi[i] - dpi[i + k - 1] < min_k:
        min_k = dpi[i] - dpi[i + k - 1]
ans = dpi[0] + k - min_k
print(ans)
 
  
 那个班主任说，你要是这都不会，就要好好想想你，是不是不太适合这个