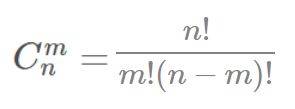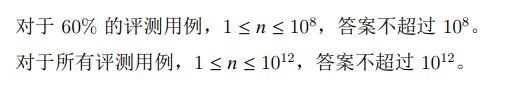【蓝桥真题】——2021年蓝桥python组省赛第2场真题+解析+代码(通俗易懂版)
![]() 大家好,我是爱学习的小蓝,欢迎交流指正~
大家好,我是爱学习的小蓝,欢迎交流指正~ ![]()
![]()
全网最详细蓝桥杯真题+解析+代码,绝对通俗易懂,一点就通!
专治各种没资源,没思路,没代码等新手入门级BUG
在文章结尾可免费领取蓝桥杯真题PDF
全文目录(1星简单 2星中等 3星困难)
⭐试题A:求余
1 真题
2 解析
3 代码
⭐试题 B: 双阶乘
1 真题
2 解析
3 代码
⭐试题 C: 格点
1 真题
2 解析
3 代码
⭐试题 D: 整数分解
1 真题
2 解析
3 代码
⭐⭐试题 E: 城邦
1 真题
2 解析
3 代码
⭐试题 F: 小平方
1 真题
2 解析
3 代码
⭐⭐试题 G: 完全平方数
1 真题
2 解析
3 代码
⭐⭐试题 H: 负载均衡
1 真题
2 解析
3 代码
⭐⭐⭐试题 I: 国际象棋
⭐⭐⭐试题 J: 完美序列
试题A:求余
1 真题
2 解析
难度系数:⭐
考察题型:python语法
蓝桥杯第一题惊现送分题!print()每题必考实锤^o^y
3 代码
print(2021%20) #输出结果:1试题 B: 双阶乘
1 真题
2 解析
难度系数:⭐
考察题型:数论
涉及知识点: 双阶乘
思路分析:
啊这,竟然遇到了小学数学题:找规律。老铁,拿捏了!
规律:后一项都比前一项少个2,2021!!=2021*2019*···*5*3*1.
从2021乘到1就OK了。
3 代码
ans=1 #初始值
for i in range(2021,0,-2):#
ans*=i #2021*2019*2017*····*3*1
print(str(ans)[-5:]) #输出结果:59375
试题 C: 格点
1 真题
2 解析
难度系数:⭐
考察题型:枚举
涉及知识点:模拟
思路分析:
一道经典的模拟题,考查列表生成式来赋值坐标,
按照题目给的条件一步步模拟,就能得到最后结果(☆▽☆)
3 代码
cnt=0 #计数器置0
for x in range(1,2022): #循环遍历每个坐标
for y in range(1,2022):
if x*y<=2021: #满足条件+1
cnt+=1
print(cnt) #输出结果:15698
试题 D: 整数分解
1 真题
2 解析
难度系数:⭐
考察题型:数论
涉及知识点:排列组合
思路分析:
方法1:五层for循环暴力破解,时间复杂度O(n^5)=2021^5次??果断换方案。
方法2:用排列组合的隔板法。
例如:3分解成2个正整数的和,有两种情况:1+2=●|●●,2+1=●●|●,
三个球,就有3-1的间隙,就需要从两个间隙选1个位置插入板,等价于
那么2021分解成5个正整数的和,相当于在2021个球●中插入4块板|,等价于
●|●|●|●|●●●●●●●●●···
套用高中学过的组合数公式,就可以求解出来了!
3 代码
#整数分解
print(2020*2019*2018*2017//4//3//2//1)
#输出结果:691677274345
试题 E: 城邦
1 真题
2 解析
难度系数:⭐⭐⭐
考察题型:图论
涉及知识点:最小生成树-并查集
思路分析:
套用最小生成树模板-并查集。
3 代码
#模板-并查集
def root(x):#查找→根节点
if x!=p[x]:
p[x]=root(p[x])
return p[x]
def union(x,y):#合并←两节点
if root(x) != root(y):
p[root(y)]=root(x)
def cost(x,y):#计算权值
s=0
while x or y:
if x%10 !=y%10:
s+=x%10+y%10
x//=10
y//=10
return s
#最小生成树
p=[i for i in range(2022)]#p:父节点列表
edge=[(i,j,cost(i,j)) for i in range(1,2022) for j in range(1,2022)]#生成边集合列表
edge.sort(key=lambda x:x[2])#sort:按权值升序排序
cnt,ans=0,0
for i in edge:
if root(i[0])!=root(i[1]) and cnt<2020:#cnt:边数=最大顶点数-1
union(i[0],i[1])
ans+=i[2]
cnt+=1
print(ans)#4046
参考链接:
Python之最小生成树 kruskal_m0_62277756的博客-CSDN博客
试题 F: 小平方
1 真题
2 解析
难度系数:⭐
考察题型:枚举
涉及知识点:模块
思路分析:
6行搞定,炒鸡easy( •̀ ω •́ )y
具体思路参考大佬视频:
蓝桥每日真题之小平方_哔哩哔哩_bilibili
3 代码
#小平方
n=int(input()) #样例输入:5
cnt=0 #计数器置0
for i in range(1,n): #1,2,3,4
if i*i%n试题 G: 完全平方数
1 真题
2 解析
难度系数:⭐⭐
考察题型:枚举 数论
涉及知识点:唯一分解定理 质数因子
思路分析:
关键是找到唯一分解定理下的奇数个的质数因子。
第一次遇见这句话可能不理解,下面我解释一下这两个名词。
唯一分解定理:一个合数(2的倍数)可以用一种最小质数的积的形式表示。
比如:6=2*3 12=2*2*3
质数因子:又是质数又是因子
质数:2,3,5,7,11······
因子:比如6的因子:1,2,3,6
6的质因子就是:2,3
具体思路:给奇数个质数因子再乘上一个该质数就可以让这个数变成完全平方数,
ans=n*x
36=12*3
36=2*2*3*3
举个栗子:对于偶数个质因子“2”,因为2*2已经配对成完全平方数4,所以不需要计数。
只需要统计奇数个质因子是一个“3”,最后n*x=12*3,答案ans=完全平方数36了。
参考思路:
蓝桥每日真题之完全平方数_哔哩哔哩_bilibili
3 代码
#完全平方数
n=int(input())#样例输入:12
x=1 #x:最小正整数
for i in range(2,int(n**0.5)+1):#循环遍历
cnt=0 #cnt:质数因子的个数
while n%i==0: #拆分因数 #12%2 6%2 3%3
cnt+=1 #1 2 3
n//=i #6 3 1
if cnt%2==1: #如果分解因子是奇数个数
x*=i #答案乘上质数因子x*=3
print(n*x) #样例输出36=12*3试题 H: 负载均衡
1 真题
2 解析
难度系数:⭐⭐⭐
考察题型:枚举
涉及知识点:模块
思路分析:
持续更新中······
参考思路:蓝桥每日真题之负载均衡_哔哩哔哩_bilibili
3 代码
#半成品QAQ
n,m=map(int,input().split())#计算机个数,任务数
v=[int(i) for i in input().split()]#每个计算机的算力
a=[[int(i) for i in input().split()] for _ in range(m)]#二维列表高效存放数据
stack=[]
heap=[]
for i in range(m):#任务0~5
heap=[i-1 if i>0 else i for i in heap]
for j in range(n):#0,1
if a[i][1]==j+1:#编号相同时
if 0 in heap:
heap.pop(0)
v[j]+=stack[0]
stack.pop(0)
res=v[j]-a[i][3] #剩余算力
if res>=0:
v[j]=res #更新算力
heap.append(a[i][2])#5s
stack.append(a[i][3])
print(res)
else:
print(-1)
试题 I: 国际象棋
持续更新中······
试题 J: 完美序列
持续更新中······
PDF百度云下载链接:
第十二届蓝桥杯大赛软件赛省赛第二场
提取码:6666
![]() 小蓝在这给大家拜年了!
小蓝在这给大家拜年了!![]()
祝看过文章的小伙伴轻轻松松拿下省一!
![]()