pytorch(三) Back Propagation 反向传播 (附详细代码+图解计算图)

Back Propagation反向传播

前言:小案例

我们有这么一个等式

$e=(a+b)\ast (b+1)$

求:e对a的导数 以及 e对b的导数

---

如果仅仅从数学的角度计算,这是非常简单的,但在深度学习中,我们会遇到许多更加复杂的计算,纯靠数学解析式来计算是十分困难的,我们需要借助 Back Propagation(反向传播)来得到答案
刚刚的等式只是一个非常简单的举例,我们要做的是把这个等式理解为一个计算图

反向传播的核心 —> 计算图

在计算图中,每一步的计算我们只能进行原子计算(不可分割的) 这里的原子计算包括加减乘除,矩阵乘法,卷积等等
下图就是 等式转化成的计算图

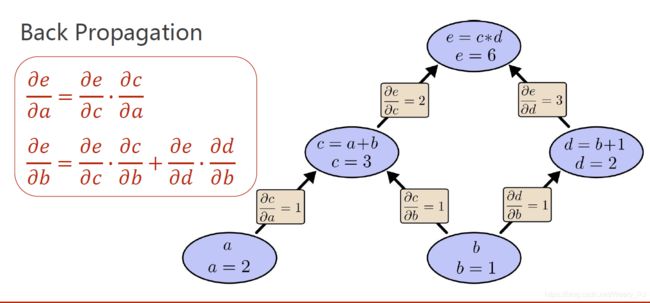
我们来简单的理解一下这个图是如何构建出来的

1. a和b通过加法得到c
2. b和1通过加法得到d
3. c和d通过乘法得到e

上面的3个步骤就是 正向传播的过程,看上去是不是十分简单

计算图构建流程

需要我们注意的是,在正向计算的过程中 ,我们不仅仅简简单单的得到 c = a + b = 3 ,与此同时, 我们还得到了c对a和b的偏导

在这里偏导数存放在a,b两个变量中,在pytorch中我们可以通过grad参数取得每个变量的偏导是多少(这将在下文中介绍)

如上图所示,在每一步计算的途中,我们都得到了变量的偏导数,那么想得到结果就变的十分简单了

如果想得到e对a的导数,那么我们仅仅需要把e到a路径上的偏导值相乘即可 链式法则

想要得到e对b的导数,我们只需要把不同路径的偏导相加即可

案例总结

根据这个简单的案例,我们实现了一个基于图的基本算法,我们可以通过它来构建十分复杂的计算图,计算出我们想要的导数,并且它具有很大的弹性,就算图改了,只要原子计算没有改变,我们还可以继续使用

正文: pytorch编程

案例:根据学习时长 推断成绩

如下图,前三组数据是我们一直的学习时间x与分数y的关系,我们需要推断出x=4的时候y是多少
这里为了方便效果演示,数据凑的很好,但在实际中,数据会有很多偏差,这就是为什么要使用深度学习

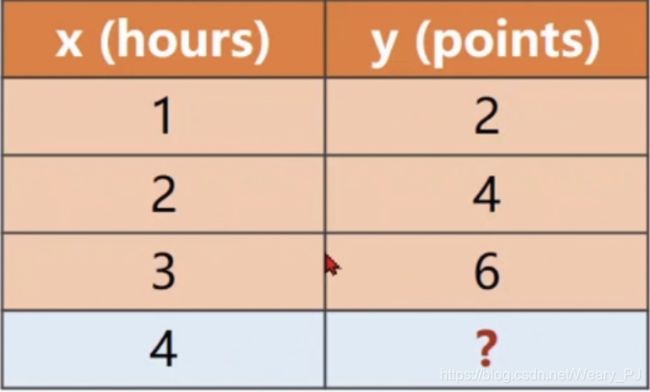
上图是我们一直的信息,依旧是一个非常简单的案例,我们通过它来了解反向传播的编程练习
通常情况下我们会假设它是一个线性模型 关于线性模型的概念请看 入口:(线性模型的博客暂未更新)
$y=w\ast x+b$
这里为了方便计算
我们就假设 $y=w\ast x$
因为根据肉眼我们显然能得到w=2,但之前也说了,这只是个举例,所以我们要模拟出训练的过程
下图是根据我们训练的线性模型得到的应该计算图

我也简单的推导了一下 模型函数为 y=x*w+b 的过程

接下来进行代码构建

1.加载数据集

import torch
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

2.权重w

这里假设w为1
w.requires_grad = True 是为了能够反向传播

w = torch.tensor([1.0])  # 假设 w = 1.0的情况
w.requires_grad = True

3.构建计算图,定义损失函数

下面两个函数就达到了上问中计算图的效果,如下

def forward(x):  # y^ = wx
    return x * w  # w是tensor 所以 这个乘法自动转换为tensor数乘 , x被转化成tensor 这里构建了一个计算图
def loss(x, y):  # 计算单个的误差 : 损失
    '''
    每调用一次loss函数,计算图自动构建一次
    :param x:
    :param y:
    :return:
    '''
    y_pred = forward(x)
    return (y_pred - y) ** 2

4.训练

这里要注意的是,每次训练的时候,我们要情况w的grad,不然将会进行累加,影响结果
更新w 是通过 $w-a\ast w^{\prime }$ 在这个步骤中我们使用了w.data = w.data -0.01 * w.grad.data
因为我们只需要对数据进行更新,如果这里没有.data的话,我们就又构建了一个计算图
最后输出结果

eli = []
lli = []
print('predict (before training)', 4, forward(4).item())
for epoch in range(100):  # 每轮输出 w的值和损失 loss
    for x, y in zip(x_data, y_data):
        l = loss(x, y)
        l.backward()  # 自动求梯度
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data    # 权重的数值更新,纯数值的修改 如果不用.data会新建计算图
        # 如果这里想求平均值 其中的累加操作 要写成sum += l.item()
        w.grad.data.zero_()     # 清空权重里梯度的数据,不然梯度会累加
    eli.append(epoch)
    lli.append(l.item())
    print('progress:', epoch, l.item())
print('Predict (after training)', 4, forward(4).item())

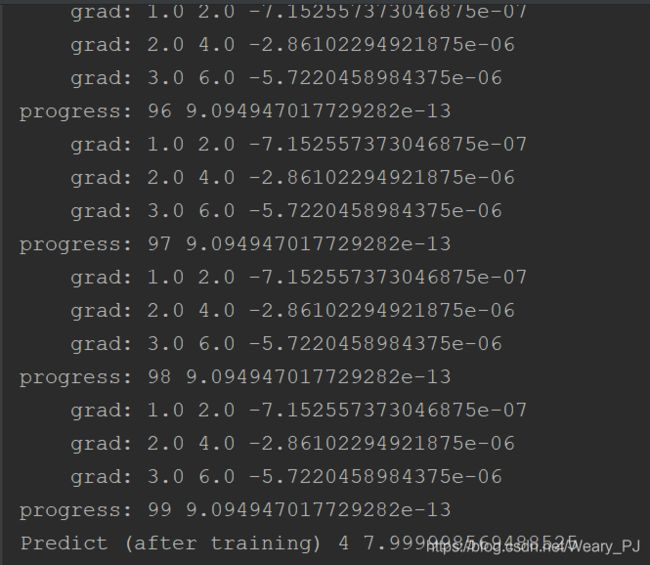
这里就展示最后几组,可以看到,经过100轮训练之后,y已经无限接近于正确的解了

5.绘制图像达

为了更加好的观察

# 绘制函数
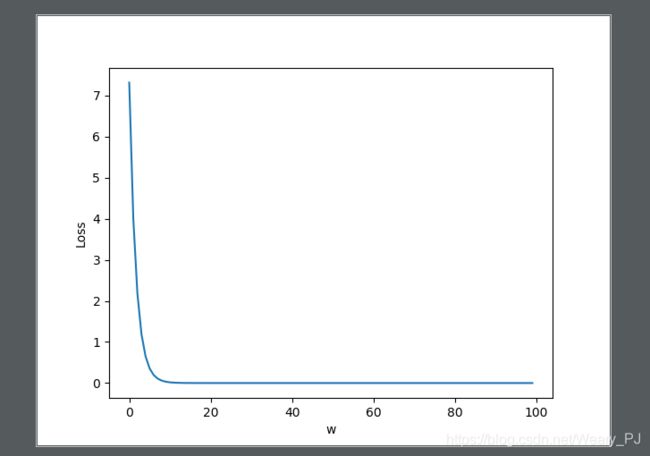
plt.plot(eli, lli)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()

学习资源来自B站,入口在这