【机器学习】一文详解异常检测算法：KNN

大家好，我们知道 sklearn 库里的 KNN 并没有直接用于异常检测，但是包含了距离计算的函数，所以我们应用PyOD中KNN库进行异常检测，里面基本上也是调用sklearn的函数进行计算，并进行了一些加工。喜欢本文记得收藏、关注、点赞。

【注】完整代码、数据、技术交流文末获取。

一、图解KNN异常检算法

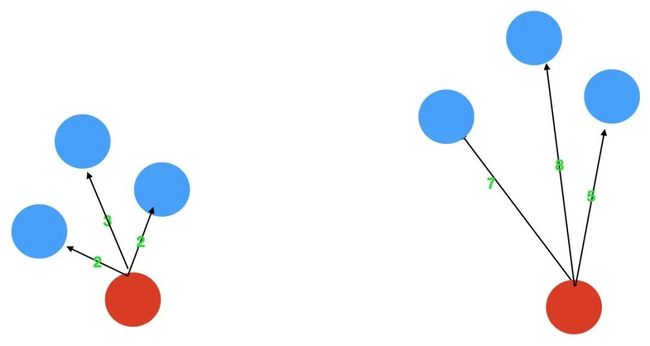
KNN怎么进行无监督检测呢，其实也是很简单的，异常点是指远离大部分正常点的样本点，再直白点说，异常点一定是跟大部分的样本点都隔得很远。基于这个思想，我们只需要依次计算每个样本点与它最近的K个样本的平均距离，再利用计算的距离与阈值进行比较，如果大于阈值，则认为是异常点，同样，为了帮助读者理解如何利用KNN思想，实现异常值的识别，我画了下面这张图。对于第一个，3个邻居的平均距离为（2+2+3）/3=2.33，对于第二点，3个邻居的平均距离为（7+8+5）/3=6.667，明显，第二个点的异常程度要高与第一个点。当然，这里除了平均距离，还可以用中位数，也可以用最大距离，通过method这个参数进行控制。

优点是不需要假设数据的分布，缺点是不适合高维数据、只能找出异常点，无法找出异常簇、你每一次计算近邻距离都需要遍历整个数据集，不适合大数据及在线应用、有人用hyper-grid技术提速将KNN应用到在线情况，但是还不是足够快，仅可以找出全局异常点，无法找到局部异常点。

KNN异常检测过程： 对未知类别的数据集中的每个点依次执行以下操作：

1. 计算当前点 与 数据集中每个点的距离

2. 按照距离递增次序排序

3. 选取与当前点距离最小的k个点

4. 计算当前点与K个邻居的距离，并取均值、或者中值、最大值三个中的一个作为异常值

1、异常实例计算

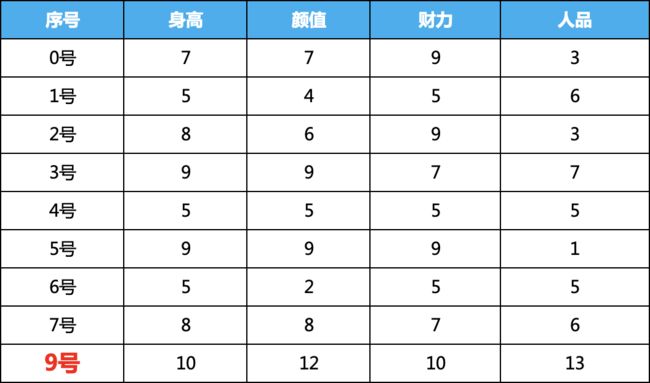
无监督，我们就要标签去掉，为了演示过程，我们引进了9号嘉宾，这个人非常自信，每一项都填的非常高，明显异常，我们的目的就是要把这种类似的异常的数据找出来。

2、距离计算和排序

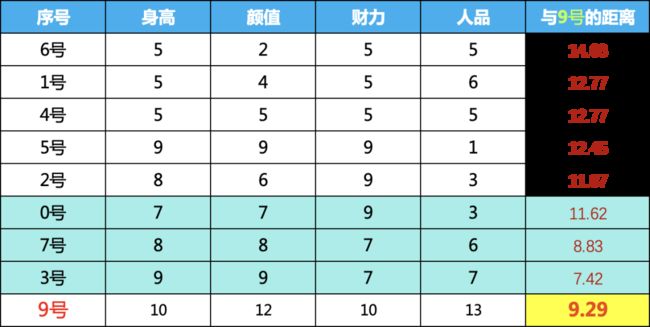
我们计算9号的异常程度，我们这里把计算和排序两步统一到一起了

先计算9号与其他样本的距离，然后排序，取最近的三个，我们计算平均距离，可以看到，9号与最近的三个邻居的平均距离是9.29

3、计算距离值

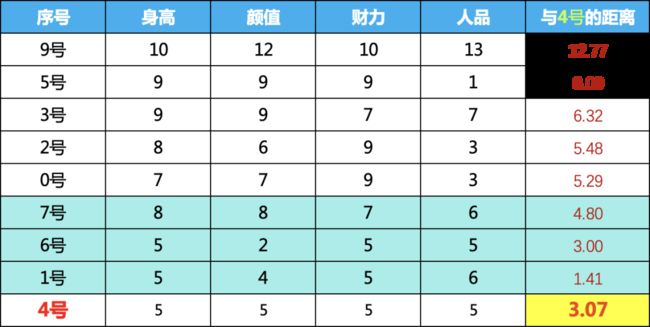
我们再计算4号嘉宾的距离，可以看到，最近的三个邻居与4号的平均距离为3.07，只是9号的三分之一，相对来说就比较正常了。当然距离计算可以用最大值，平均值，中位数三个，算法中通过method这个参数进行调节。

我们依次计算，就可以得到每个样本3个邻居的平均距离了，越高的越异常，我们也可以用Python的包来检测下我们计算的对不对。

import numpy as np  
X_train = np.array([
[7,  7,  9,  3],
[5,  4,  5,  6],
[8,  6,  9,  3],
[9,  9,  7,  7],
[5,  5,  5,  5],
[9,  9,  9,  1],
[5,  2,  5,  5],
[8,  8,  7,  6],
[10,10,  12,  13]])
# import kNN分类器
from pyod.models.knn import KNN

# 训练一个kNN检测器
clf_name = 'kNN'
# 初始化检测器clf
clf = KNN( method='mean', n_neighbors=3, )
clf.fit(X_train) 

# 返回训练数据X_train上的异常标签和异常分值
# 返回训练数据上的分类标签 (0: 正常值, 1: 异常值)
y_train_pred = clf.labels_  
y_train_pred
array([0, 0, 0, 0, 0, 0, 0, 0, 1])

# 返回训练数据上的异常值 (分值越大越异常)
y_train_scores = clf.decision_scores_  
y_train_scores
array([2.91709951, 3.01181545, 3.09299219, 4.16692633, 3.07001503,
       4.25784112, 3.98142397, 3.24271326, 9.42068891])

我们自己计算的平均距离为9.29，系统算的9.42，有一点点的差异，可能是哪里加了一个微调的系数，大家可以探索下。

二、KNN异常检测算法应用

上面大概知道了KNN怎么进行异常检测的，现在我们找个具体的案例，看看更加明细的参数以及实现的过程，有个更加立体的感觉，并且学完能够应用起来。

源码地址：https://pyod.readthedocs.io/en/latest/_modules/pyod/models/knn.html#KNN

1、算法基本用法

地址：https://pyod.readthedocs.io/en/latest/pyod.models.html#module-pyod.models.knn

pyod.models.knn.KNN(contamination=0.1, 
                    n_neighbors=5, 
                    method='largest', 
                    radius = 1.0, 
                    algorithm='auto', 
                    leaf_size=30, 
                    metric='minkowski', 
                    p=2, 
                    metric_params=None, 
                    n_jobs=1, 
                    **kwargs)

2、参数详解

contamination：污染度,contamination : float in (0., 0.5), optional (default=0.1)数据集的污染量，即数据集中异常值的比例。在拟合时用于定义决策函数的阈值。如果是“自动”，则确定决策函数阈值，如原始论文中所示。_在版本0.20中更改：_默认值contamination将从0.20更改为’auto’0.22。

n_neighbors：选取相邻点数量

method：‘largest’、‘mean’、‘median’

• largest：使用与第k个相邻点的距离作为异常得分

• mean：使用k个相邻点距离的平均值作为异常得分

• median：使用k个相邻点距离的中值作为异常得分

radius : radius_neighbors使用的参数空间半径

algorithm：找到最近的k个样本

• kd_tree：依次对K维坐标轴，以中值切分，每一个节点是超矩形，适用于低维（<20时效率最高）

• ball_tree：以质心c和半径r分割样本空间，每一个节点是超球体，适用于高维（kd_tree高维效率低）

• brute：暴力搜索

• auto：通过 fit() 函数拟合，选择最适合的算法；如果数据稀疏，拟合后会自动选择brute，参数失效

leaf_size：kd_tree和ball_tree中叶子大小，影响构建、查询、存储，根据实际数据而定。树叶中可以有多于一个的数据点，算法在达到叶子时在其中执行暴力搜索即可。如果leaf size 趋向于 N（训练数据的样本数量），算法其实就是 brute force了。如果leaf size 太小了，趋向于1，那查询的时候 遍历树的时间就会大大增加。

metric：距离计算标准,距离标准图例

• euclidean：欧氏距离（p = 2）

• manhattan：曼哈顿距离（p = 1）

• minkowski：闵可夫斯基距离

p : metric参数，默认为2

metric_params : metric参数

n_jobs : 并行作业数，-1时，n_jobs为CPU核心数。

3、属性详解

decision_scores： 数据X上的异常打分，分数越高，则该数据点的异常程度越高

threshold： 异常样本的个数阈值，基于contamination这个参数的设置，总量最多等于n_samples * contamination

labels: 数据X上的异常标签，返回值为二分类标签（0为正常点，1为异常点）

4、方法详解

fit(X): 用数据X来“训练/拟合”检测器clf。即在初始化检测器clf后，用X来“训练”它。

fit_predict_score(X, y): 用数据X来训练检测器clf，并预测X的预测值，并在真实标签y上进行评估。此处的y只是用于评估，而非训练

decision_function(X): 在检测器clf被fit后，可以通过该函数来预测未知数据的异常程度，返回值为原始分数，并非0和1。返回分数越高，则该数据点的异常程度越高

predict(X): 在检测器clf被fit后，可以通过该函数来预测未知数据的异常标签，返回值为二分类标签（0为正常点，1为异常点）

predict_proba(X): 在检测器clf被fit后，预测未知数据的异常概率，返回该点是异常点概率

当检测器clf被初始化且fit(X)函数被执行后，clf就会生成两个重要的属性：

decision_scores: 数据X上的异常打分，分数越高，则该数据点的异常程度越高

5、案例分析

KNN算法专注于全局异常检测，所以无法检测到局部异常。首先，对于数据集中的每条记录，必须找到k个最近的邻居。然后使用这K个邻居计算异常分数。最 大： 使用到第k个邻居的距离作为离群值得分；平均值： 使用所有k个邻居的平均值作为离群值得分；中位数： 使用到k个邻居的距离的中值作为离群值得分

在实际方法中后两种的应用度较高。然而，分数的绝对值在很大程度上取决于数据集本身、维度数和规范化。参数k的选择当然对结果很重要。如果选择过低，记录的密度估计可能不可靠。（即过拟合）另一方面，如果它太大，密度估计可能太粗略。K值的选择通常在10-50这个范围内。所以在分类方法中，选择一个合适的K值，可以用交叉验证法。

#导入
from pyod.models.knn import KNN
from pyod.utils.data import generate_data
from pyod.utils.data import evaluate_print
from pyod.utils.example import visualize

#参数设置
contamination = 0.1  # percentage of outliers
n_train = 200  # number of training points
n_test = 100  # number of testing points

# 数据生成
X_train, y_train, X_test, y_test = generate_data(\
    n_train=n_train, n_test=n_test,\ 
    contamination=contamination)

# import kNN分类器
from pyod.models.knn import KNN

# 训练一个kNN检测器 初始化检测器clf
clf_name = 'kNN'
clf = KNN() 
# 使用X_train训练检测器clf
clf.fit(X_train)

# 返回训练数据X_train上的异常标签和异常分值
# 返回训练数据上的分类标签 (0: 正常值, 1: 异常值)
y_train_pred = clf.labels_

# 返回训练数据上的异常值 (分值越大越异常)
y_train_scores = clf.decision_scores_  

# 用训练好的clf来预测未知数据中的异常值
y_test_pred   = clf.predict(X_test)
y_test_scores = clf.decision_function(X_test)

对识别结果可视化

# 模型可视化
visualize(clf_name, 
          X_train, 
          y_train, 
          X_test, 
          y_test, 
          y_train_pred,
          y_test_pred, 
          show_figure=True, 
          save_figure=False
         )

推荐文章

• 李宏毅《机器学习》国语课程(2022)来了

• 有人把吴恩达老师的机器学习和深度学习做成了中文版

• 上瘾了，最近又给公司撸了一个可视化大屏(附源码)

• 如此优雅，4款 Python 自动数据分析神器真香啊

• 梳理半月有余，精心准备了17张知识思维导图，这次要讲清统计学

• 香的很，整理了20份可视化大屏模板

技术交流

欢迎转载、收藏、有所收获点赞支持一下！

目前开通了技术交流群，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友

• 方式①、发送如下图片至微信，长按识别，后台回复：加群；
• 方式②、添加微信号：dkl88191，备注：来自CSDN
• 方式③、微信搜索公众号：Python学习与数据挖掘，后台回复：加群