《深入 C 语言和程序运行原理》18 极致优化（上）：如何实现高性能的 C 程序？（学习笔记）

仅作为本人学习《深入 C 语言和程序运行原理》的学习笔记，原课程链接：极客时间《深入 C 语言和程序运行原理》——于航

如何衡量程序的运行性能？

宽泛地讲，程序运行性能可以体现在内存使用率和运行时间上。

程序效率是指计算机资源能否有效地使用，即系统运行时尽量占用较少空间，却能用较快速度完成规定功能。

——百度百科

技巧一：利用高速缓存

现代计算机体系中，L1、L2、L3（甚至 L4）一般分别对应 CPU 芯片上的三个不同级别的高速缓存，这些缓存的数据读写速度依次降低，但容量依次升高。

一级缓存即L1 Cache。集成在CPU内部中，用于CPU在处理数据过程中数据的暂时保存。由于缓存指令和数据与CPU同频工作，L1级高速缓存缓存的容量越大，存储信息越多，可减少CPU与内存之间的数据交换次数，提高CPU的运算效率。但因高速缓冲存储器均由静态RAM组成，结构较复杂，在有限的CPU芯片面积上，L1级高速缓存的容量不可能做得太大。

L2缓存位于CPU与内存之间的临时存储器，它的容量比内存小但交换速度快。在缓存中的数据是内存中的一小部分，但这一小部分是短时间内CPU即将访问的，当CPU调用大量数据时，就可避开内存直接从缓存中调用，从而加快读取速度。

L3 Cache(三级缓存)，分为两种，早期的是外置，现在的都是内置的。而它的实际作用即是，L3缓存的应用可以进一步降低内存延迟，同时提升大数据量计算时处理器的性能。

——百度百科

下面是一张 Inter CPU 的架构图，形象展现了三种不同级别缓存的关系：（现在个人水印无法去除了，更新了？）

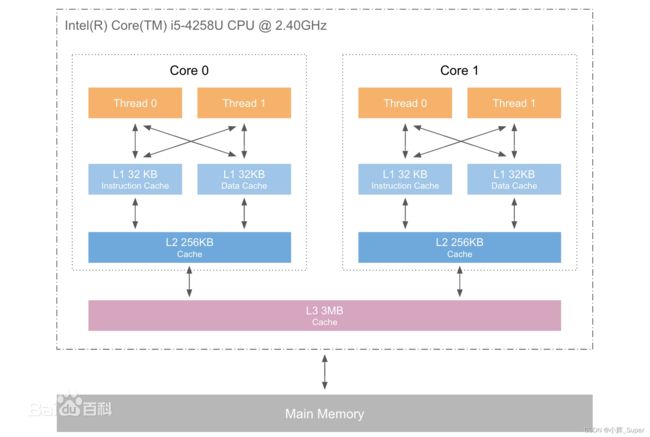
上面的 CPU 是 x86 架构的，ARM 架构的一些高性能 CPU 也有多个不同级别的缓存。（本文不讨论 ARM 平台，仅考虑 x86 下的程序优化）

L1 到 L3 缓存直接由 CPU 硬件进行管理，CPU 取数据时，访问顺序是 L1 -> L2 -> L3 -> 内存，如果在 L1 找到了数据，就不会去 L2 找，这样可以加快数据的读取速度。

高速缓存之所以能提升性能，主要是因为“局部性原理”。

程序局部性原理，是计算机科学术语，指程序在执行时呈现出局部性规律，即在一段时间内，整个程序的执行仅限于程序中的某一部分。相应地，执行所访问的存储空间也局限于某个内存区域。局部性原理又表现为：时间局部性和空间局部性。

——百度百科

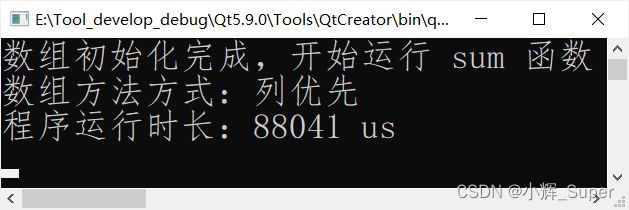
这里给出一个例子，定义一个函数来操作二维数组（由于系统对栈空间有限制，一般默认为 10K，所以局部空间不能定义大数组，需要在全局空间定义，不然可能导致程序无法运行），分别使用行优先和列优先的方式遍历数组。
（下面只是函数代码，完整测试代码见文末）

#define M 10240       // 二维数组行数
#define N 1024        // 二维数组列数
int array[M][N];      // 大数组需要声明为全局变量
#define ROW_MAJOR  1  // 是否开启行优先

int sum(int a[M][N])
{
  int i, j, sum = 0;
#if ROW_MAJOR  // 先遍历行，再遍历列
  for (i = 0; i < M; ++i)
    for (j = 0; j < N; ++j)
      sum += a[i][j];
#else          // 先遍历列，再遍历行
  for (j = 0; j < N; ++j)
    for (i = 0; i < M; ++i)
      sum += a[i][j];
#endif
  return sum;
}

如果使用行优先来遍历数组，则符合程序局部原理（因为数组数据是按照"行优先”的方式存储的），CPU 在一级缓存中就能读取到大部分数组数据，测试代码中运行该函数用时约 22 ms，

如果选择列优先的方式遍历数组，CPU 每次读取数组数据时，需要频繁地跨越一大段空间，当前后要读取两个数据不在同级缓存中，CPU 还需要从低层次缓存（如 2 级缓存）中拷贝数据到高层次缓存（如 1 级缓存），这大大减缓了程序的运行，测试代码中运行该函数用时 88 ms，效率是行优先方式的 1/4 。

因此，为了更好地利用 CPU 高速缓存，你可以参考这些原则来编写代码：

• 尽量确保定义的局部变量能够被多次引用；
• 再循环结构中，比较短的步长访问数据；
• 对于数组结构，使用行优先遍历；
• 循环体越小，循环迭代次数越多，则局部性越好。
  

——原文

技巧二：代码内联

在计算机科学中，内联函数（有时称作在线函数或编译时期展开函数）是一种编程语言结构，用来建议编译器对一些特殊函数进行内联扩展（有时称作在线扩展）；也就是说建议编译器将指定的函数体插入并取代每一处调用该函数的地方（上下文），从而节省了每次调用函数带来的额外时间开支。但在选择使用内联函数时，必须在程序占用空间和程序执行效率之间进行权衡，因为过多的比较复杂的函数进行内联扩展将带来很大的存储资源开支。另外还需要特别注意的是对递归函数的内联扩展可能引起部分编译器的无穷编译。

——百度百科

inline 是 C99 标准引入的一个关键字，它可以建议编译器将函数内联到调用处。这样的好处在于，可以省去函数调用过程中需要进行的函数栈创建和销毁过程，以节省 CPU 时钟周期。这种方式通常用在函数被多次调用的场景。

虽然内联函数可以提高程序执行效率，但是不合理的使用可能会导致可执行文件增大，所以内联只适用于那些函数体较小，且会被多次调用的函数。

不过我简单测试了一下发现无论是否使用内联函数，程序执行效率都没太大变化，这可能是编译器没接受我将函数内联的建议，或是因为编译器在高优化等级的情况下，会默认采用内联来对代码进行优化。

技巧三：restrict 关键字

restrict是c99标准引入的，它只可以用于限定和约束指针，并表明指针是访问一个数据对象的唯一且初始的方式.即它告诉编译器，所有修改该指针所指向内存中内容的操作都必须通过该指针来修改,而不能通过其它途径(其它变量或指针)来修改;这样做的好处是,能帮助编译器进行更好的优化代码,生成更有效率的汇编代码.如 int *restrict ptr, ptr 指向的内存单元只能被 ptr 访问到，任何同样指向这个内存单元的其他指针都是未定义的，直白点就是无效指针。restrict 的出现是因为 C 语言本身固有的缺陷，C 程序员应当主动地规避这个缺陷，而编译器也会很配合地优化你的代码.

——百度百科

技巧四：消除不必要的内存引用

register修饰符暗示编译程序相应的变量将被频繁地使用，如果可能的话，应将其保存在CPU的寄存器中，以加快其存储速度。

——百度百科

我用原文的示例代码来编译运行，发现优化后的函数并没有运行得更快，这可能与数组太大存在一定关系（但是数组太小，运行时间直接变 0 us），也有可能是 register 修饰符自身的问题（见下文引用部分）。

#define LEN (1024 * 1024 * 64)
int array[LEN];
#if 1  // 优化前的函数
void foo(int* dest)
{
    *dest = 0;
    for(int i = 0; i < LEN; i++)
    {
        *dest = *dest + array[i];
    }
}

#else  // 使用 register 修饰符优化频繁读写的变量
void foo(int* dest)
{
    register int tmp = 0;
    for(int i = 0; i < LEN; i++)
    {
        tmp = tmp + array[i];
    }
    *dest = tmp;
}
#endif

但是使用register修饰符有几点限制。
首先，register变量必须是能被CPU所接受的类型。这通常意味着register变量必须是一个单个的值，并且长度应该小于或者等于整型的长度。不过，有些机器的寄存器也能存放浮点数。
其次，因为register变量可能不存放在内存中，所以不能用“&”来获取register变量的地址。
由于寄存器的数量有限，而且某些寄存器只能接受特定类型的数据（如指针和浮点数），因此真正起作用的register修饰符的数目和类型都依赖于运行程序的机器，而任何多余的register修饰符都将被编译程序所忽略。
在某些情况下，把变量保存在寄存器中反而会降低程序的运行速度。因为被占用的寄存器不能再用于其它目的；或者变量被使用的次数不够多，不足以装入和存储变量所带来的额外开销。
早期的C编译程序不会把变量保存在寄存器中，除非你命令它这样做，这时register修饰符是C语言的一种很有价值的补充。然而，随着编译程序设计技术的进步，在决定哪些变量应该被存到寄存器中时，C编译环境能比程序员做出更好的决定。实际上，许多编译程序都会忽略register修饰符，因为尽管它完全合法，但它仅仅是暗示而不是命令。

——百度百科

---

附录

技巧1对应测试代码

#include 
#include         //struct timeval
#include 


#define M 10240       // 二维数组行数
#define N 1024        // 二维数组列数
int array[M][N];      // 大数组需要声明为全局变量
#define ROW_MAJOR  0  // 是否开启行优先

int sum(int a[M][N])
{
  int i, j, sum = 0;
#if ROW_MAJOR  // 先遍历行，再遍历列
  for (i = 0; i < M; ++i)
    for (j = 0; j < N; ++j)
      sum += a[i][j];
#else          // 先遍历列，再遍历行
  for (j = 0; j < N; ++j)
    for (i = 0; i < M; ++i)
      sum += a[i][j];
#endif
  return sum;
}

int main()
{
    struct timeval tv_start, tv_end;
    long int duration = 0;         //运行时长
    int i = 0, j = 0;

    // 数组初始化（随意）
    for(i = 0; i < M; i++)
        for(j = 0; j < N; j++)
            array[i][j] = i % 10;

    printf("数组初始化完成，开始运行 sum 函数\r\n");
    gettimeofday(&tv_start,NULL);   //获取1970-1-1到现在的时间保存到timeval变量

    // 要测试的代码
    int ret = sum(array);

    gettimeofday(&tv_end,NULL);
//    printf("函数运行结果：%d\r\n", ret);

    if(tv_end.tv_sec == tv_start.tv_sec)
        duration = tv_end.tv_usec - tv_start.tv_usec;
    else
        duration = tv_end.tv_usec + 1000000 - tv_start.tv_usec;
//    printf("start=%ld,end=%ld\r\n", tv_start.tv_usec, tv_end.tv_usec);
    printf("数组方法方式：%s\n", ROW_MAJOR ? "行优先" : "列优先");
    printf("程序运行时长：%ld us\n", duration);

    return 0;
}