【视觉SLAM十四讲源码解读】匹配的3D空间点对应用矩阵分解求位姿并用g2o优化

运行结果

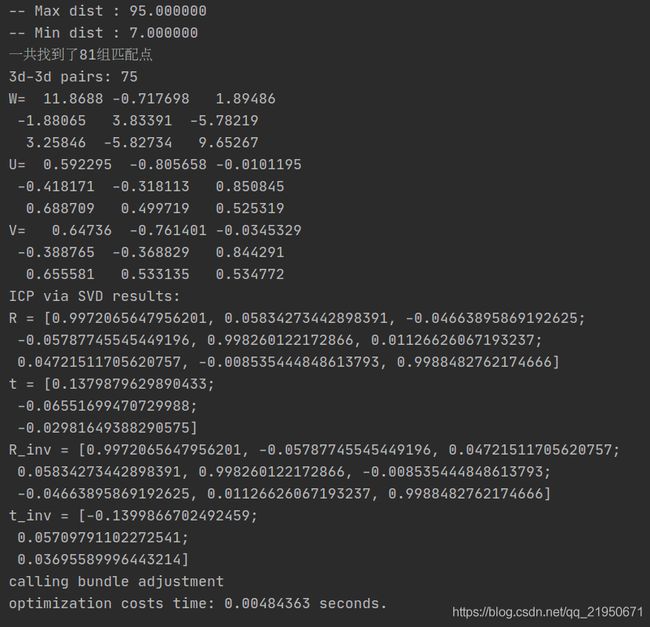
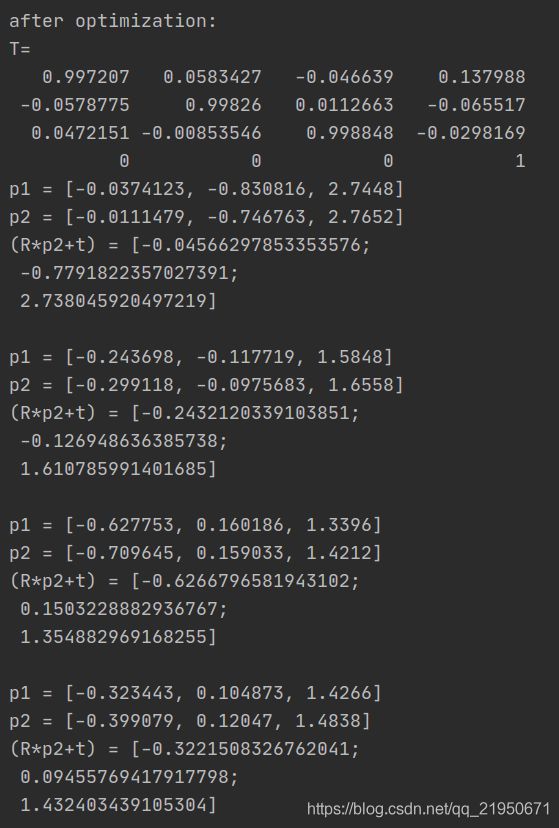
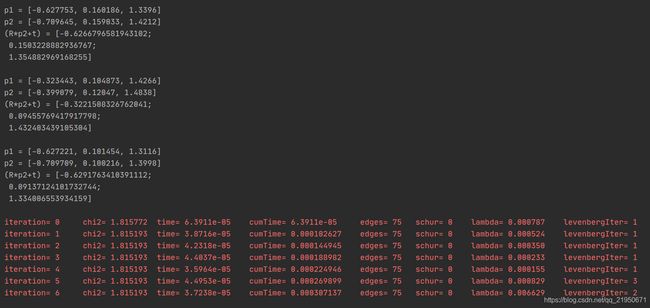
源码解读

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

void find_feature_matches(
        const Mat &img_1, const Mat &img_2,
        std::vector<KeyPoint> &keypoints_1,
        std::vector<KeyPoint> &keypoints_2,
        std::vector<DMatch> &matches);

Point2d pixel2cam(const Point2d &p, const Mat &K);

void pose_estimation_3d3d(
        const vector<Point3f> &pts1,
        const vector<Point3f> &pts2,
        Mat &R, Mat &t
);

void bundleAdjustment(
        const vector<Point3f> &points_3d,
        const vector<Point3f> &points_2d,
        Mat &R, Mat &t
);


/**
 * vertex and edges used in g2o ba
 * template 　
 * D:维度Dimension　T:类型EstimateType
 * Templatized BaseVertex
 * D  : minimal dimension of the vertex, e.g., 3 for rotation in 3D
 * T  : internal type to represent the estimate, e.g., Quaternion for rotation in 3D
 * 6:优化变量最小维度
 * Sophus::SE3d:优化变量SE(3)李代数位姿表示的类型
 * 结合这个程序学习:g2oCurveFitting.cpp
 */
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    virtual void setToOriginImpl() override {
        // Sophus::SE3d()初始化单位矩阵
        _estimate = Sophus::SE3d();
    }

    // left multiplication on SE3(李群左乘微小扰动对应李代数求导加法更新变量)
    virtual void oplusImpl(const double *update) override {
        Eigen::Matrix<double, 6, 1> update_eigen;
        update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
        // pose->setEstimate(Sophus::SE3d());
        _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;
    }

    virtual bool read(istream &in) override {}

    virtual bool write(ostream &out) const override {}
};

/**
 * template 
 * g2o::BaseUnaryEdge<3, Eigen::Vector3d, VertexPose>
    误差模型 模板参数<观测值维度，类型，顶点类型>
    观测值是像素
    顶点是相机位姿
    定义边，表示投影误差
    结合这个程序学习:g2oCurveFitting.cpp
 */
class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, VertexPose> {
public:
    // Eigen库为了使用SSE加速,内存分配上使用了128位的指针,但实际分配的可能时64位或32位与内存对齐有关系
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
    // 定义边的计算方式:输入是_point(point)
    EdgeProjectXYZRGBDPoseOnly(const Eigen::Vector3d &point) : _point(point) {}
    // edge->setMeasurement(Eigen::Vector3d(pts1[i].x, pts1[i].y, pts1[i].z));
    virtual void computeError() override {
        const VertexPose *pose = static_cast<const VertexPose *> ( _vertices[0] );
         /**
          * _measurement 的类型是　BaseUnaryEdge<3, Eigen::Vector3d
          * pose->estimate() 是优化的位姿态　就是优化的顶点
          * pose->setEstimate(Sophus::SE3d());
          */
        _error = _measurement - pose->estimate() * _point;
    }
    /**
     * 定义优化策略
     * 计算雅克比矩阵就是求每一个待优化变量的偏导数
     */
     //edge->setMeasurement(Eigen::Vector3d(pts1[i].x, pts1[i].y, pts1[i].z));
    virtual void linearizeOplus() override {
        VertexPose *pose = static_cast<VertexPose *>(_vertices[0]);
        Sophus::SE3d T = pose->estimate();
        Eigen::Vector3d xyz_trans = T * _point;
        /**
         * Identity　_jacobianOplusXi.matrix()
          -1         -0         -0          0   -1.73533 -0.0797886
          -0         -1         -0    1.73533          0 -0.0812386
          -0         -0         -1  0.0797886  0.0812386          0
         * hat　_jacobianOplusXi.matrix()
          -1        -0        -0         0   -1.2273  0.155471
          -0        -1        -0    1.2273         0 -0.145699
          -0        -0        -1 -0.155471  0.145699         0
         */
        // 单位矩阵初始化
        _jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();
        // cout << "Identity　_jacobianOplusXi.matrix()\n" << _jacobianOplusXi.matrix() << endl;
        // xyz_trans 向量转换到反对称矩阵
        _jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans);
        // cout << "hat　_jacobianOplusXi.matrix()\n" << _jacobianOplusXi.matrix() << endl;

    }

    bool read(istream &in) {}

    bool write(ostream &out) const {}

protected:
    Eigen::Vector3d _point;
};

int main(int argc, char **argv) {
    if (argc != 1) {
        cout << "usage: pose_estimation_3d3d img1 img2 depth1 depth2" << endl;
        return 1;
    }
    //-- 读取图像
    Mat img_1 = imread("/home/q/projects/slambook2/ch7/1.png", CV_LOAD_IMAGE_COLOR);
    Mat img_2 = imread("/home/q/projects/slambook2/ch7/2.png", CV_LOAD_IMAGE_COLOR);

    vector<KeyPoint> keypoints_1, keypoints_2;
    vector<DMatch> matches;
    find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
    cout << "一共找到了" << matches.size() << "组匹配点" << endl;

    // 建立3D点 深度图为16位无符号数，单通道图像
    Mat depth1 = imread("/home/q/projects/slambook2/ch7/1_depth.png", CV_LOAD_IMAGE_UNCHANGED);
    // 深度图为16位无符号数，单通道图像
    Mat depth2 = imread("/home/q/projects/slambook2/ch7/2_depth.png", CV_LOAD_IMAGE_UNCHANGED);
    Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
    vector<Point3f> pts1, pts2;

    for (DMatch m:matches) {
        ushort d1 = depth1.ptr<unsigned short>(int(keypoints_1[m.queryIdx].pt.y))[int(keypoints_1[m.queryIdx].pt.x)];
        ushort d2 = depth2.ptr<unsigned short>(int(keypoints_2[m.trainIdx].pt.y))[int(keypoints_2[m.trainIdx].pt.x)];
        if (d1 == 0 || d2 == 0)   // bad depth
            continue;
        Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K);
        Point2d p2 = pixel2cam(keypoints_2[m.trainIdx].pt, K);
        float dd1 = float(d1) / 5000.0;
        float dd2 = float(d2) / 5000.0;
        pts1.push_back(Point3f(p1.x * dd1, p1.y * dd1, dd1));
        pts2.push_back(Point3f(p2.x * dd2, p2.y * dd2, dd2));
    }

    cout << "3d-3d pairs: " << pts1.size() << endl;
    Mat R, t;
    pose_estimation_3d3d(pts1, pts2, R, t);
    cout << "ICP via SVD results: " << endl;
    cout << "R = " << R << endl;
    cout << "t = " << t << endl;
    cout << "R_inv = " << R.t() << endl;
    cout << "t_inv = " << -R.t() * t << endl;

    cout << "calling bundle adjustment" << endl;

    bundleAdjustment(pts1, pts2, R, t);

    // verify p1 = R * p2 + t
    for (int i = 0; i < 5; i++) {
        cout << "p1 = " << pts1[i] << endl;
        cout << "p2 = " << pts2[i] << endl;
        cout << "(R*p2+t) = " <<
             R * (Mat_<double>(3, 1) << pts2[i].x, pts2[i].y, pts2[i].z) + t
             << endl;
        cout << endl;
    }
}

void find_feature_matches(const Mat &img_1, const Mat &img_2,
                          std::vector<KeyPoint> &keypoints_1,
                          std::vector<KeyPoint> &keypoints_2,
                          std::vector<DMatch> &matches) {
    //-- 初始化
    Mat descriptors_1, descriptors_2;
    // used in OpenCV3
    Ptr<FeatureDetector> detector = ORB::create();
    Ptr<DescriptorExtractor> descriptor = ORB::create();
    // use this if you are in OpenCV2
    // Ptr detector = FeatureDetector::create ( "ORB" );
    // Ptr descriptor = DescriptorExtractor::create ( "ORB" );
    Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
    //-- 第一步:检测 Oriented FAST 角点位置
    detector->detect(img_1, keypoints_1);
    detector->detect(img_2, keypoints_2);

    //-- 第二步:根据角点位置计算 BRIEF 描述子
    descriptor->compute(img_1, keypoints_1, descriptors_1);
    descriptor->compute(img_2, keypoints_2, descriptors_2);

    //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
    vector<DMatch> match;
    // BFMatcher matcher ( NORM_HAMMING );
    matcher->match(descriptors_1, descriptors_2, match);

    //-- 第四步:匹配点对筛选
    double min_dist = 10000, max_dist = 0;

    //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
    for (int i = 0; i < descriptors_1.rows; i++) {
        double dist = match[i].distance;
        if (dist < min_dist) min_dist = dist;
        if (dist > max_dist) max_dist = dist;
    }

    printf("-- Max dist : %f \n", max_dist);
    printf("-- Min dist : %f \n", min_dist);

    //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
    for (int i = 0; i < descriptors_1.rows; i++) {
        if (match[i].distance <= max(2 * min_dist, 30.0)) {
            matches.push_back(match[i]);
        }
    }
}

Point2d pixel2cam(const Point2d &p, const Mat &K) {
    return Point2d(
            (p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
            (p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
    );
}

// 线性代数方法 SVD 求解 位姿
void pose_estimation_3d3d(const vector<Point3f> &pts1, const vector<Point3f> &pts2, Mat &R, Mat &t) {
    // 下面计算用到的公式是：第七章 SVD 7.50 公式  计算两组点的质心
    Point3f p1, p2;     // center of mass
    int N = pts1.size();
    //  pts1[-0.037412327, -0.83081567, 2.7448001;
    //  -0.24369837, -0.11771931, 1.5848;
    //  -0.62775266, 0.16018634, 1.3396;...

    //  pts2[-0.01114786, -0.74676317, 2.7651999;
    //  -0.2991184, -0.097568251, 1.6558;
    //  -0.70964509, 0.15903255, 1.4212;...
    for (int i = 0; i < N; i++) {
        p1 += pts1[i];
        p2 += pts2[i];
    }
    //  p1 = [-2.82142, -7.38721, 123.886]
    //  p2 = [-7.0357, -4.31404, 126.563]
    p1 = Point3f(Vec3f(p1) / N);
    p2 = Point3f(Vec3f(p2) / N);
    //  p1[-0.0376189, -0.0984961, 1.65181]
    //  p2[-0.0938094, -0.0575205, 1.68751]

    // remove the center 也就是归一化
    vector<Point3f> q1(N), q2(N);
    for (int i = 0; i < N; i++) {
        q1[i] = pts1[i] - p1;
        q2[i] = pts2[i] - p2;
    }
    //  q1[0.0002065897, -0.73231959, 1.0929893;
    //  -0.20607945, -0.019223213, -0.06701076;
    //  -0.59013373, 0.25868243, -0.3122108;

    // q2[0.082661502, -0.6892426, 1.0776908;
    //  -0.20530903, -0.040047709, -0.031709075;
    //  -0.61583573, 0.21655309, -0.26630902;


    // compute q1*q2^T
    // 原理是：第一版教材 公式 7.56
    Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
    for (int i = 0; i < N; i++) {
        W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();
    }
    cout << "W=" << W << endl;
    //  W=  11.8688   -0.717698   1.89486
    //      -1.88065   3.83391   -5.78219
    //       3.25846  -5.82734    9.65267

    // SVD on W  对W进行SVD分解求旋转矩阵R 原理是第一版 公式 7.58
    Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();

    cout << "U=" << U << endl;
    cout << "V=" << V << endl;

    Eigen::Matrix3d R_ = U * (V.transpose());
    if (R_.determinant() < 0) {
        R_ = -R_;
    }
    // 原理第一版教材公式: 7.53
    Eigen::Vector3d t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);

    // convert to cv::Mat
    R = (Mat_<double>(3, 3) <<
                            R_(0, 0), R_(0, 1), R_(0, 2),
            R_(1, 0), R_(1, 1), R_(1, 2),
            R_(2, 0), R_(2, 1), R_(2, 2)
    );
    t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}


/**
 * @brief 非线性BA 求解 位姿
 * @param pts1
 * @param pts2
 * @param R
 * @param t
 */
void bundleAdjustment(const vector<Point3f> &pts1, const vector<Point3f> &pts2, Mat &R, Mat &t) {
    // 构建图优化，先设定g2o
    typedef g2o::BlockSolverX BlockSolverType;
    typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
    // 梯度下降方法，可以从GN, LM, DogLeg 中选
    auto solver = new g2o::OptimizationAlgorithmLevenberg(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
    g2o::SparseOptimizer optimizer;     // 图模型
    optimizer.setAlgorithm(solver);   // 设置求解器
    optimizer.setVerbose(true);       // 打开调试输出

    // vertex 定义图的顶点
    VertexPose *pose = new VertexPose(); // camera pose
    pose->setId(0);
    // 设置图的顶点也就是要优化变量是 SE3欧式群->变换矩阵                                                                                                                                                                                                                                                                                                                                                                                                                                                             变换矩阵
    pose->setEstimate(Sophus::SE3d());
    optimizer.addVertex(pose);

    // edges 定义图的边
    for (size_t i = 0; i < pts1.size(); i++) {
        EdgeProjectXYZRGBDPoseOnly *edge = new EdgeProjectXYZRGBDPoseOnly(Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z));
        edge->setVertex(0, pose);
        edge->setMeasurement(Eigen::Vector3d(pts1[i].x, pts1[i].y, pts1[i].z));
        edge->setInformation(Eigen::Matrix3d::Identity());
        optimizer.addEdge(edge);
    }

    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    optimizer.initializeOptimization();
    optimizer.optimize(10);
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "optimization costs time: " << time_used.count() << " seconds." << endl;

    cout << endl << "after optimization:" << endl;
    cout << "T=\n" << pose->estimate().matrix() << endl;

    // convert to cv::Mat
    Eigen::Matrix3d R_ = pose->estimate().rotationMatrix();
    Eigen::Vector3d t_ = pose->estimate().translation();
    R = (Mat_<double>(3, 3) <<
                            R_(0, 0), R_(0, 1), R_(0, 2),
            R_(1, 0), R_(1, 1), R_(1, 2),
            R_(2, 0), R_(2, 1), R_(2, 2)
    );
    t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}