【LeetCode】第290场单周赛 --- 记录一次AK周赛
目录
- 写在前面
-
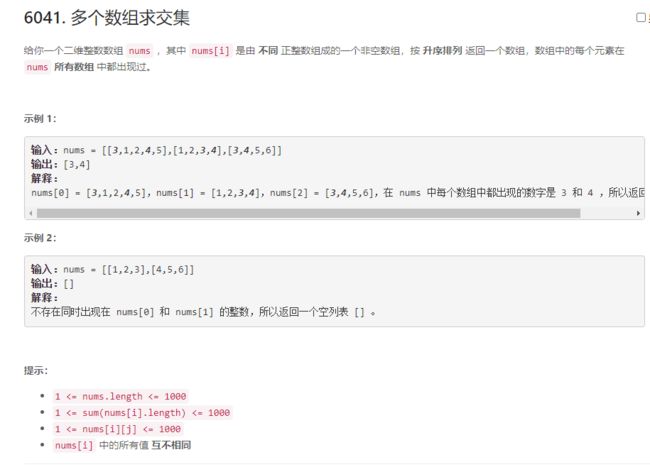
- 题1: 6041. 多个数组求交集
-
- 题目描述
- 解题思路
- 代码编写(Java版本)
- 题2: 6042. 统计圆内格点数目
-
- 题目描述
- 解题思路
- 代码编写(Java版本)
- 题3: 6043. 统计包含每个点的矩形数目
-
- 题目描述
- 思路一:二分搜索
- 思路二:二维偏序+树状数组
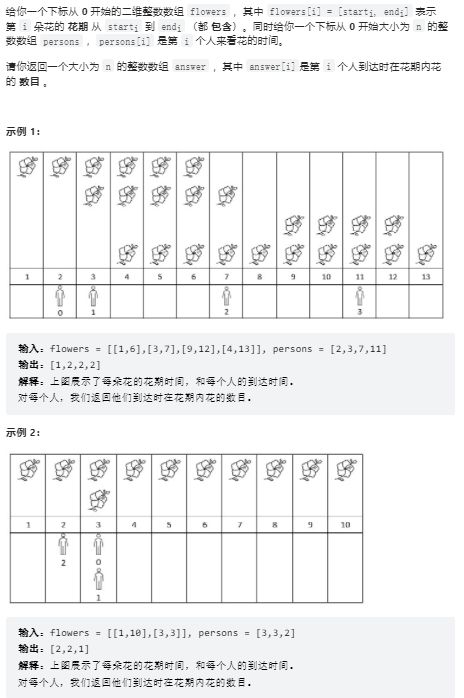
- 题4: 6044. 花期内花的数目
-
- 题目描述
- 思路一:排序+二分
- 思路二:排序
- 写在最后
写在前面
Hello朋友们,我是秋刀鱼,一只活跃于Java区与算法区的新人博主~

欢迎大家加入高校算法学习社区: https://bbs.csdn.net/forums/Suanfa,社区里大佬云集,大家互相交流学习!
今天给大家带来LeetCode 290场单周赛的题目解析,分享一下我解题时的思考过程。如果觉得还不错的话务必三连支持一下博主哦
主页:秋刀鱼与猫期待你的支持与关注~
题1: 6041. 多个数组求交集
题目描述
题目传送门
解题思路
非常简单的一道题目!
数据的区间范围是: [ 1 , 1000 ] [1,1000] [1,1000],该数据量下可以定义数组记录 [ 1 , 1000 ] [1,1000] [1,1000]每一个数出现的次数。最后按照升序将出现次数为 nums 长度的数输出即可。
代码编写(Java版本)
class Solution { public List<Integer> intersection(int[][] nums) { int len = nums.length; int[] t = new int[1001]; for (int[] num : nums) { for (int val : num) { t[val]++; } } List<Integer> ans = new ArrayList<>(); for (int i = 0; i <= 1000; ++i) { if (t[i] == len) { ans.add(i); } } return ans; } }
题2: 6042. 统计圆内格点数目
题目描述
题目传送门
提示:
1 <= circles.length <= 200circles[i].length == 31 <= xi, yi <= 1001 <= ri <= min(xi, yi)
解题思路
题目中已经给定了圆心 x , y x,y x,y 以及圆半径 r r r 的取值范围,因此可以通过暴力枚举的方式枚举所有可能包含在圆内部区间的点,通过判断枚举点与任意圆心的距离是否小于该圆心对应的半径即可。
代码编写(Java版本)
class Solution { public int countLatticePoints(int[][] circles) { int res = 0, len = circles.length; for (int i = 0; i <= 200; i++) { for (int j = 0; j <= 200; j++) { for (int k = 0; k < len; k++) { int a = circles[k][0] - i, b = circles[k][1] - j, c = circles[k][2]; if (a * a + b * b <= c * c) { res++; break; } } } } return res; } }
题3: 6043. 统计包含每个点的矩形数目
题目描述
题目传送门
提示:
1 <= rectangles.length, points.length <= 5 * 10e4rectangles[i].length == points[j].length == 21 <= li, xj <= 10e91 <= hi, yj <= 100- 所有
rectangles互不相同 。- 所有
points互不相同 。
思路一:二分搜索
核心思路
对于一个点是否能够被矩阵所包含,只需要判断该矩阵右上角坐标: ( x , y ) (x,y) (x,y) 是否都大于等于该点的坐标,如果满足则该点一定能够被矩阵包含。现在将问题转换为求解矩阵右上角坐标 ( x , y ) (x,y) (x,y) 均大于等于该点坐标 ( x i , y i ) (x_i,y_i) (xi,yi) 的矩阵个数。
解题方法
细心的小伙伴可能会发现, y y y 的取值范围为: [ 1 , 100 ] [1,100] [1,100] 。那么假设当前 p o i n t s points points 点的坐标为 ( x i , y i ) (x_i,y_i) (xi,yi) ,于是符合要求的矩阵坐标 ( x , y ) (x,y) (x,y) 一定满足 y ∈ [ y i , 100 ] y\in[y_i,100] y∈[yi,100] 。那么只需要遍历 [ y i , 100 ] [y_i,100] [yi,100] 区间内的所有矩阵坐标,满足 x i < = x x_i<=x xi<=x 的坐标符合题目的要求,将符合要求矩阵的数量输出即是最终答案。
但是上述思路因为数据量太大因此会超时,需要进行算法优化。
如果能够将所有 y y y 相同的矩阵坐标的 x x x 值按照 x x x 递增的次序存储在一个数组中,当遍历 [ y i , 100 ] [y_i,100] [yi,100] 时只需要将对应数组的值按照二分的方式查找第一个大于等于 x i x_i xi 的位置 l l l, n − l n-l n−l的值就是我们需要寻找的值。
此时的时间复杂度为: O ( y ⋅ l g ( x ) ⋅ l e n g t h ) O(y\cdot lg(x) \cdot length) O(y⋅lg(x)⋅length) 符合题目要求,这道题就这样搞定了!

思路一代码(Java版本)
class Solution {
public int[] countRectangles(int[][] rect, int[][] p) {
int n = p.length;
int[] ans = new int[n];
Arrays.sort(rect, (a, b) -> (a[1] != b[1] ? a[1] - b[1] : a[0] - b[0]));
// pos存放每一个 y 对应的 x 坐标
List<int[]>[] pos = new ArrayList[105];
for (int i = 1; i <= 100; i++) pos[i] = new ArrayList<>();
for (int[] x : rect) pos[x[1]].add(x);
for (int i = 0; i < n; i++) {
int sum = 0;
// 遍历 y 坐标
for (int j = p[i][1]; j <= 100; j++) {
List<int[]> cur = pos[j];
int l = 0, r = cur.size();
// 二分查找实现 upper_bound
while (l < r) {
int mid = l + (r - l) / 2;
if (cur.get(mid)[0] >= p[i][0] && cur.get(mid)[1] >= p[i][1]) r = mid;
else l = mid + 1;
}
sum += cur.size() - l;
}
ans[i] = sum;
}
return ans;
}
}
思路二:二维偏序+树状数组
二维偏序的定义
对于坐标轴中的点 i i i 其坐标为 ( x i , y i ) (x_i,y_i) (xi,yi) ,坐标中其余点的坐标满足 x < = x i x<=x_i x<=xi 且 y < = y i y<=y_i y<=yi 的点数量称为这个点 i i i 的偏序。
例如:下面图中: C C C 点的偏序为 0 , B B B 点的偏序为 2, A A A 点的偏序为 1 图片转自
求解二维偏序
***本题目中核心思路就是求解偏序,只不过原本偏序的定义需要满足小于等于的条件,而在本题中需要满足大于等于的条件,因此本题对偏序的定义有做修改。***
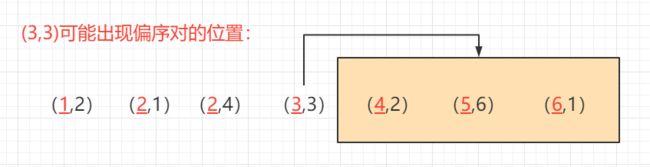
属于偏序的坐标 ( x , y ) (x,y) (x,y) 一定满足 x > = x i x>=x_i x>=xi 且 y > = y i y>=y_i y>=yi ,其实对于这两个条件我们可以优先满足一个:将二维坐标 ( x , y ) (x,y) (x,y) 按照 x x x 的递增顺序排序,例如下图所示:
那么就拿坐标 ( 3 , 3 ) (3,3) (3,3)来说,其偏序对只有可能出现其后方(因为需要满足 x x x >= x i x_i xi )
很显然橙色方框中的坐标不全都能够组成偏序对,因为偏序对还需要满足第二个条件: y y y >= y i y_i yi ,该条件应该如何判断呢 ?

这里我使用 树状数组 来解决。对于 ( 3 , 3 ) (3,3) (3,3) 后方的点的 y y y 坐标建立树状数组,树状数组中存储 y y y 出现的次数,定义方法 g e t ( y ) get(y) get(y) 获取 [ 1 , y ] [1,y] [1,y] 坐标数量的总和。
为了判断满足 y > = y i y>=y_i y>=yi 的总数,定义 m a x Y maxY maxY 为 y y y 坐标的最大值,因此只需要在树状数组中查询: g e t ( m a x Y ) − g e t ( y i − 1 ) get(maxY) - get(y_i-1) get(maxY)−get(yi−1) 就是该点 ( x i , y i ) (x_i,y_i) (xi,yi) 的偏序值。
解题思路
有了上面的思路,不难发现其实本题就是求解 p o i n t s points points 数组中每一个点在坐标轴中的偏序值。
按照上面的思路,将所有
rectangles与points的点加入到数组中,加入时需要区分点是从rectangles中加入还是points中加入。
rectangles加入的点需要被更新到树状数组中,points加入的点需要记录其原来在points中的位置,不更新到树状数组。加入完毕后按照 x x x 做降序排序,从第一个点开始遍历,确保树状数组中保存的是 x > = x i x>=x_i x>=xi 坐标的 y y y 信息。
- 如果是
points中的点,需要通过树状数组中的值求出其偏序对并更新到points数组中。- 如果是
rectangles中的点,需要将其 y y y 的值更新到树状数组中。最终遍历完所有点后返回 points 即是最终结果。
思路二代码(Java版本)
class Solution {
class Node {
int x, y, status,from;
Node(int x, int y, int status, int from) {
this.x = x;
this.y = y;
this.status = status;
this.from = from;
}
}
// 记录最大的 y 值
int maxY;
int[] tree;
int lowbit(int val) {
return val & (-val);
}
void update(int idx) {
for (; idx <= maxY; idx += lowbit(idx)) {
tree[idx]++;
}
}
int get(int idx) {
int sum = 0;
for (; idx > 0; idx -= lowbit(idx)) {
sum += tree[idx];
}
return sum;
}
public int[] countRectangles(int[][] rectangles, int[][] points) {
List<Node> nodes = new ArrayList<>();
int[] ret = new int[points.length];
for (int[] rectangle : rectangles) {
nodes.add(new Node(rectangle[0], rectangle[1], -1,-1));
maxY = Math.max(maxY, rectangle[1]);
}
int idx = 0;
for (int[] point : points) {
nodes.add(new Node(point[0], point[1], 1,idx));
maxY = Math.max(maxY, point[1]);
++idx;
}
nodes.sort((a,b)->{
return a.x == b.x ? b.y - a.y : b.x - a.x;
});
tree = new int[maxY + 1];
for (Node node : nodes) {
// 更新树状数组
if (node.status == -1) {
update(node.y);
}
// 求出偏序值
else{
ret[node.from] = get(maxY) - get(node.y - 1);
}
}
return ret;
}
}
题4: 6044. 花期内花的数目
题目描述
题目传送门
提示:
1 <= flowers.length <= 5 * 10e4flowers[i].length == 21 <= starti <= endi <= 10e91 <= persons.length <= 5 * 10e41 <= persons[i] <= 10e9
思路一:排序+二分
解题方法
如果将
flowers中每一个区间段称为:[begin,end],那么对于 i i i 时间点,假定其能观赏花的数目为: n u m num num。那么对于 i i i 时间点,如果在 [ 0 , i ] [0,i] [0,i]这段时间中,一共有 n n n 朵花期开始;如果在 [ 0 , i − 1 ] [0,i-1] [0,i−1]这段时间中,一共有 m m m 朵花花期结束,那么此时时间点 i i i 能够欣赏花的数目 n u m = n − m num = n-m num=n−m
因此为了快速获取 n , m n,m n,m 的值,可以将每一个花期的开始时间、结束时间存放在两个 List 中并按照升序排序。对于 i i i 时间点的 n , m n,m n,m 值只需要通过二分查找就可以快速获取,时间复杂度为: O ( n ⋅ l n g ) O(n\cdot lng) O(n⋅lng)
思路一代码(Java版本)
class Solution { public int lower_bound(List<Integer> list, int key) { int l = 0; int r = list.size(); while (l < r) { int m = (l + r) / 2; if (list.get(m) < key) { l = m + 1; }else{ r = m; } } return l; } public int upper_bound(List<Integer> list, int key) { int l = 0; int r = list.size(); while (l < r) { int m = (l + r) / 2; if (list.get(m) <= key) { l = m + 1; }else{ r = m; } } return l; } public int[] fullBloomFlowers(int[][] flowers, int[] persons) { List<Integer> begin = new ArrayList<>(); List<Integer> end = new ArrayList<>(); for (int[] flower : flowers) { begin.add(flower[0]); end.add(flower[1]); } begin.sort((a,b)->{ return a - b;}); end.sort((a, b) -> { return a - b; }); int n = begin.size(); int len = persons.length; for (int i = 0; i < len; ++i) { int cur = persons[i]; int n = upper_bound(begin, cur); int m = lower_bound(end, cur); persons[i] = beginNum - endNum; } return persons; } }
思路二:排序
解题方法
将花期分为
begin与end分别表示花期的开始时间与结束时间,将其与persons中查询的时间值x存储并按照递增的顺序排序。同时存储一个标记位来表示该时间值来自于
begin、end、person中的哪一个。我在代码中用INF表示该值为花期的开始时间;-INF表示为花期的结束时间;其余情况表示这是一个请求时间。那么从开始位置进行遍历,使用一个变量
tmp存储当前遍历的时间点花朵的数目。
- 如果遍历到的值为花期开始时间,即:
p.second == INF,则让tmp加一表示进入一个新的花期。- 如果遍历到的值为花期结束时间,即:
p.second == -INF,则让tmp减一表示离开一个新的花期。- 否则表示该遍历的时间点为
persons中查询的时间点,将当前的tmp存储。最终返回结果。
思路一代码(C++版本)
class Solution {
typedef pair pii;
const int INF = 1e9+5;
public:
vector fullBloomFlowers(vector>& flowers, vector& persons) {
vector vec;
for (auto &f : flowers) vec.push_back(pii(f[0], -INF)), vec.push_back(pii(f[1], INF));
for (int i = 0; i < persons.size(); i++) vec.push_back(pii(persons[i], i));
sort(vec.begin(), vec.end());
vector ans(persons.size());
int tmp = 0;
for (pii p : vec) {
if (p.second == -INF) tmp++;
else if (p.second == INF) tmp--;
else ans[p.second] = tmp;
}
return ans;
}
};
写在最后
总的来说本次周赛的难度一般,并没有太难的题,甚至我觉得最后一题是我做过最简单的一道困难题。不过虽然题目简单但还是需要高度地集中注意力,稍有差错就可能因为忽略题目给定的条件而 WA。
最后感谢你能够耐心看完