2020蓝桥杯省赛第一场A组(C/C++)个人题解

结果填空

A. 跑步训练

【解题】
按题意模拟即可，先按分钟变化，当体力不足600时跳出循环，按比例再加上相应的秒数即可。

#include
#include
#include
using namespace std;
int main()
{
	int i,j;
	int ti=0;
	int power=10000;
	while(1)
	{
		if(power>=600)
		{
			power-=600;
			ti+=60;
		}
		else break;
		
		power+=300;
		ti+=60;
	}
	ti+=power/10;//每分钟减600,均匀减小,故每秒减600/60=10; 
	printf("%d\n",ti);
	return 0;
}

//ans==3880;

ans:3880

B. 合并检测

【解题】
[更新解法] 由于该国民众的被感染率为1%，并且为均匀分布，那么相当于100个人里面有1个感染，因此当k>=100的值的时候，合并检测中必定有阳性，会导致所有人都要单独检测，因此k的遍历返回可以缩小至 [1,100) 区间中。

取100个人，则有1人是被感染的。
假设分成k组，则每组有[(100/k)向上取整]个人。
则所需试剂盒数量为：
	f(k)=k+[100/k](其中[]表示向上取整)
其中前半部分是k组合并检测需要k个试剂盒;后半项是被感染者所在的组所有人要再单独检测。
遍历k∈[1,100)即可。

#include
#include
#include
using namespace std;

int main(){
	int k;
	int minn=101;//最少的试剂盒数量;
	int minpos=0;//取最小值时的k的值; 
	//f(k)=k+[100/k]
	for(k=1;k<100;k++){
		int temp;
		if(100%k==0) temp=k+100/k; 
		else temp=k+100/k+1;
		if(temp<minn){
			minn=temp;
			minpos=k;
		}
	}
	printf("%d\n",minpos);
	return 0;
} 

//ans:10

ans:10

C. 分配口罩

【解题】
这个题就是把数组分成两个部分，求两部分和最小值的包装版本，可以用暴力dfs也可以dp(0-1背包作背包容量为sum/2的dp)，结果填空且只有15个数，直接暴力搜即可。

#include
#include
#include
#include 
using namespace std;
typedef long long ll;
ll num[15]={9090400,8499400,5926800,8547000,4958200,4422600,5751200,4175600,6309600,5865200,6604400,4635000,10663400,8087200,4554000};
ll minn=0x3f3f3f3f;
ll sum;

void dfs(int pos,ll now)
{
	if(pos>=15)
	{
		minn=min(minn,abs(sum-2*now));
		return ;
	}
	dfs(pos+1,now+num[pos]);//选 
	dfs(pos+1,now); //不选 
}

int main()
{
	int i,j;
	int n,m;
	sum=0;
	for(i=0;i<15;i++)
	{
		sum+=num[i];
	}
	dfs(0,0);
	printf("%lld\n",minn);
	return 0;
 } 
 
 //ans==2400; 

ans:2400

D. 矩阵

【解题】
DP进行方案数计数，dp(i,j)表示前i个数选其中j个放入第一行，转移策略如代码中注释所示。

#include
#include
#include
using namespace std;
const int maxn=2500;
int dp[maxn][maxn];//dp[i][j]表示前i个数放其中j个到第一行的方案数; 
int main()
{
	int i,j;
	memset(dp,0,sizeof(dp));
	dp[1][1]=1;//1肯定放到第一行(若放到第二行不可能比第一行大)
	//维护dp表的下三角即可(j>i的上三角无意义)
	//dp策略:
	//1.数字放在第一行肯定可以,后面遍历的数字越来越大;
	//2.数字放在第二行的条件是目前第一行的数字比第二行多,
	//	因为若目前少,则之后肯定得有更大的数放到第一行,与要求冲突 
	for(i=2;i<=2020;i++)
	{
		for(j=1;j<=i;j++)
		{
			dp[i][j]=(dp[i][j]+dp[i-1][j-1])%2020;//放到第一行; 
			if(i-j<=j)//i-j为放第二行的数字数,即放第二行的数字数小于第一行的数字数的情况(此时i是正要遍历的,所以等号可取) 
			{
				//放到第二行; 
				dp[i][j]=(dp[i][j]+dp[i-1][j])%2020;
			} 
		}
	}
	printf("%d\n",dp[2020][1010]);
	return 0;
 } 
 //ans==1340

ans:1340

E. 完美平方数

【解题】
感谢评论区大佬提供的思路，打表发现所述完美平方数必须为各数位值均属于{0,1,4,9}组成的数。
因此可以用0,1,4,9在各数位枚举去构造，这样时间复杂度是4^len(其中len是数字的长度)，但是这样还是无法在有限时间内找到第2020个数，只能找到大概第900个数，后面速度就比较慢了，因为第2020个数估计出现在len=19的位置，因此需要4 ^ 19的时间…

#include
#include
#include
#include
using namespace std;
typedef long long ll;
int base[]={0,1,4,9};
ll ans;
int tot=0;
bool fin=false;

//用{0,1,4,9}为各数位值去构造. 
void dfs(int pos,int len,ll sum){
	if(pos>len){
		if((ll)(sqrt(sum))*(ll)(sqrt(sum))==sum){
			tot++;
			printf("%d %lld\n",tot,sum);
		}
		if(tot==2020){
			ans=sum;
			fin=true;
		}
		return ;
	} 
	int start;
	if(pos==1) start=1;//最高位不能为0,否则会重复计数. 
	else start=0;
	for(int i=start;i<4&&!fin;i++){
		dfs(pos+1,len,sum*10+base[i]);
	}
	return ;
}

int main()
{
	ll i;
	tot=4;//单个位数的先初始出来(0,1,4,9);
	ll ans;
	int len=2; 
	while(tot<2020)
	{
		dfs(1,len,0);
		len++;
	} 
	printf("%lld\n",ans);
	return 0;
 } 

 //ans:

打表程序:

#include
#include
#include
using namespace std;
typedef long long ll;

//打表程序 
int main()
{
	ll i;
	int tot=7;//现在已找到第7个(0,1,4,9,49,100,144);
	i=13;//12*12==144,从13*13开始即可 
	while(tot<50)
	{
		ll num=i*i;
		while(num!=0)
		{
			ll now=num%10;
			if(now!=0&&now!=1&&now!=4&&now!=9)//数位不是完全平方数 
			{
				break;
			}
			num/=10;
		}
		if(num==0)
		{
			tot++;
			printf("%lld\n",i*i);
		}
		i++;
	} 
	return 0;
 } 

程序题

F. 解码

【解题】
这题也是思路很直接，若是数字再补上num-1个字母即可。

#include
#include
#include
using namespace std;
const int maxn=105;
char s1[maxn];
char s2[maxn*maxn];
int main()
{
	int i,j;
	scanf("%s",s1);
	char now=s1[0];
	s2[0]=now;
	int len=0;
	for(i=1;i<strlen(s1);i++)
	{
		if(s1[i]>='0'&&s1[i]<='9')
		{
			for(j=1;j<s1[i]-'0';j++) 
			{
				s2[++len]=now;	
			}
		}
		else
		{
			now=s1[i];
			s2[++len]=now;
		}
	} 
	s2[++len]='\0';
	printf("%s\n",s2);
	return 0;
 } 

G. 走方格

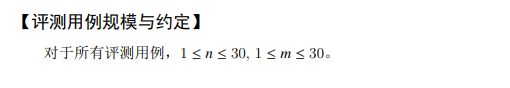
【解题】
经典DP计数题，加了一个行号列号偶数不能走的限制。

#include
#include
#include
using namespace std;
const int maxn=50;
int dp[maxn][maxn];

int main()
{
	int i,j;
	int n,m;
	scanf("%d%d",&n,&m);
	if(n%2==0&&m%2==0) printf("0\n");
	else
	{
		memset(dp,0,sizeof(dp));
		dp[1][1]=1;
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=m;j++)
			{
				if(i%2==0&&j%2==0) dp[i][j]=0;
				else
				{
					dp[i][j]=max(dp[i][j],dp[i-1][j]+dp[i][j-1]);
				}
			}
		}
		printf("%d\n",dp[n][m]);
	}
	return 0;
 } 

H. 整数小拼接

【解题】
将各数字以字符串形式输入，按长度排序，对每次遍历得到的两个数字，若两数字的长度之和小于K的长度，直接ans+2，若两数的长度之和大于K的长度，直接break出遍历(因为按长度排序了，现在的长度大于了K，之后的长度肯定也大于K)，这样其实是O(n^2)+一点优化（对于n为10 ^ 5的数据量其实是可以卡的，此处有没有更优的方法？）

#include
#include
#include 
#include
using namespace std;
const int maxn=1e5+6;
typedef long long ll;
struct node{
	char s[20];
	int len;
}a[maxn];
char str[20];

bool cmp(node a,node b)
{
	return a.len<b.len;
}

ll get_value(char* s)
{
	ll value=0;
	for(int i=0;i<strlen(s);i++)
	{
		value=value*10+s[i]-'0';
	}
	return value;
}

int main()
{
	int i,j,k;
	int n;
	/*
	以字符串形式输入:
	若lenlenk直接出来; 
	*/ 
	scanf("%d %s",&n,str);
	int l=strlen(str);
	for(i=1;i<=n;i++)
	{
		scanf("%s",&a[i].s);
		a[i].len=strlen(a[i].s);
		//printf("%s",a[i].s);
	}
	ll ans=0;
	ll str_v=get_value(str);
	//printf("%lld\n",str_v); 
	sort(a+1,a+1+n,cmp);
	for(i=1;i<=n;i++)
	{
		bool fin=false;
		for(j=i+1;j<=n;j++)
		{
			if(a[i].len+a[j].len<l)
			{
				ans+=2;
			}
			else if(a[i].len+a[j].len==l)
			{
				ll v1=get_value(a[i].s);
				ll v2=get_value(a[j].s);
				ll va=v1*pow(10,a[j].len)+v2;
				ll vb=v2*pow(10,a[i].len)+v1;
				if(va<=str_v) ans++;
				if(vb<=str_v) ans++;
			}
			else
			{
				fin=true;
				break;//因为按长度从小到大排,现在不行之后的肯定也不行; 
			}
		}
		if(fin) break;
	}
	printf("%lld\n",ans);
	return 0;
}

I. 超级胶水

【解题】
这道题第一眼是贪心，第二眼是区间DP，但瞄了一下数据范围，贪心或区间DP应该都不能拿满(估计O(n^2))，手算了一波好像按照花费是乘积，重量变成两者之和这种约束是无论怎么选总花费都一样的…都为各重量两两乘积的和。
数学归纳法证明：

设总花费为f
当n=2时，设石头重量分别为a,b，则f=a*b正确;
当n=3时，设石头重量分别为a,b,c，
	则所有合并方式分别为:
		f1=a*b+(a+b)*c=a*b+a*c+b*c;
		f2=a*c+(a+c)*b=a*b+a*c+b*c;
		f3=b*c+(b+c)*a=a*b+a*c+b*c;
		f=f1=f2=f3，正确;
假设当n=k时结论正确,设石头重量分别为a1,a2,...ak
	即f=a1*a2+a1*a3+...+a1*an+...+a(k-1)*ak
当n=k+1时，设石头重量分别为a1,a2,...ak,a(k+1)
	无论将a(k+1)在哪一步进行合并，
	其都可以看成是a(k+1)与ai的一个置换(1<=i<=k)
	设a(k+1)与其中的ai进行了置换，
	石头表示为(a1,a2,...,a(k+1),...ak),ai
	对于前面括号中的部分，由假设的n=k的情况可以得到:
		f1=a1*a2+...a1*an+...a(k+1)*a(i+1)+...+a(k+1)*ak+...+a(k-1)*ak
	对前面括号的合并后可以看成剩两堆石头X,ai，
	其中X的重量为a1+a2+...+a(k+1)+...+ak
	对数量为2的情况，
		花费f2=(a1+a2+...+a(k+1)+...+ak)*ai
			 =a1*ai+a2*ai+...ak*ai+a(k+1)*ai
	故当n=k+1时，
	总花费为f=f1+f2=a1*a2+...+a1*a(k+1)+...+ak*a(k+1)
	因此假设正确。

故得到各重量两两乘积的和即可，时间复杂度O(n)

#include
#include
#include
using namespace std;
const int maxn=1e5+6;
typedef long long ll;
ll num[maxn];
ll sum,ans;

int main()
{
	int i,j;
	int n;
	scanf("%d",&n);
	for(i=1;i<=n;i++)
	{
		scanf("%d",&num[i]); 
	}
	sum=num[1];
	ans=0;
	for(i=2;i<=n;i++)
	{
		ans+=sum*num[i]; 
		sum+=num[i];//前i个石头的重量和; 
	}
	printf("%lld\n",ans);
	return 0;
}

J. 网络分析

【解题】
感谢评论区大佬提供的思路，采用类似带权并查集的思想可以在O(m*log(m))的时间完成（朴素的并查集+遍历更新需要O(n * m)的时间复杂度）。
思路为：相较于朴素并查集，增加一个value数组存储当前节点到其父节点的边权,这里边权value[i]的含义是节点i的当前存储信息量，借助find函数路径压缩的时候同时更新。每次在某节点发送信息时，方法是找到根节点，建立一个虚节点作为根节点的父节点，该虚节点成为新的根节点。
（其实就是借助树的层次来区别不同节点所累加的信息量，越靠近根节点的节点是越晚加入的，可以画图理解）

#include
#include
#include
using namespace std;
const int maxn=2e5+5;
int f[maxn],value[maxn];
//其中,f[i]表示的是节点i的父节点id,value[i]记录节点i与其父节点之间的边权.
 
int find(int x){
	if(x==f[x]) return x;
	else{
		int z=f[x];//记录路径压缩前原父节点的id
		f[x]=find(f[x]);
		value[x]+=value[z];
		return f[x]; 
	}	
}

int main(){
	int i,j;
	int n,m;
	scanf("%d%d",&n,&m);
	for(i=1;i<=n;i++){
		f[i]=i;
		value[i]=0;
	}
	int op,a,b;
	int tot=n;//当前总节点数,每次发送测试信息时,建立虚节点作为新的根节点 
	for(i=1;i<=m;i++){
		scanf("%d%d%d",&op,&a,&b);
		//op==1表示连通节点a和节点b;
		//op==2表示在节点p发送一条大小为t的信息;
		if(op==1){
			int fa=find(a);
			int fb=find(b);
			if(fa!=fb){
				f[fa]=fb;
				value[fa]=0; //连通后两节点还没有发送信息,因此边权初始化为0. 
			}
		} 
		else{
			int fp=find(a);
			tot++;//建立虚节点
			value[tot]=0;
			f[tot]=tot;
			f[fp]=tot;
			value[fp]=b; 
		}
	}
	for(i=1;i<=tot;i++){
		int temp=find(i);//最后再更新一次,将根节点权值更新到各个节点. 
	}
	for(i=1;i<=n;i++){
		if(i!=n) printf("%d ",value[i]);
		else printf("%d\n",value[i]);
	}
	//printf("%d\n",ans);
	return 0;
}