机器学习之分类方法K近邻(KNN)

一、原理

1、基本思想及步骤

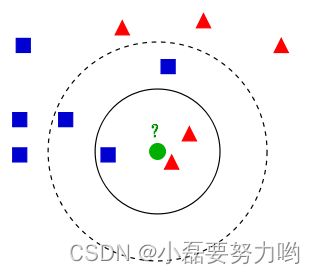
• k近邻(KNN)是一种基本分类与回归方法，属于有监督学习（带有标签）。分类问题中的k紧邻，输入的是实例的特征向量（特征空间的点），输出的是实例的类别，可以取多类。它的原理很简单，就是服从多数原则。详细来说：给定一个数据集，其中的实例类别已定，在训练数据集中找到与目标实例最近的k各实例，这k个实例若大多数属于某个类别，就把目标实例归分为这个类别。看个例子，就明白了。
• 蓝色方块和红色三角属于给定的数据集，绿色圆圈为待分类，现在让我们分析以下这个绿色圆圈到底属于哪个类？
  • 若k=3，则与绿色圆圈最近的有两个红色三角和一个蓝色方块，根据服从多数原则，我们将绿色圆圈划分到红色三角里；若k=5，则与绿色圆圈最近的有两个红色三角和三个蓝色方块，根据服从多数原则，我们将绿色圆圈划分到蓝色方块里；由此可知，待分类数据到底属于哪一类根据k值的不同而不同。

• 步骤：
• 输入：训练集 $T=(x_i,y_1),(x_2,y_2),\dots \dots ,(x_n,y_n)$，其中$x_i$为实例的特征向量，$y_i$ 是实例的真实类别；待分类数据特征向量为x。
• 输出：待分类x的类别y。
• （1）根据给定的距离度量，在训练集T中找出距离实例x最近的k个点。
• （2）在这k个点中根据分类原则（如多数表决）决定x的类别。
• k近邻的特殊情况是k=1的情形，成为最近邻算法。
• 现在我们就基本上理解K近邻的原理了，很简单吧，但其中的K值怎么选取，是K近邻的一大难点，还有两点间的距离选择哪个距离度量和分类决策原则（大部分运用多数表决规则 = 经验风险最小化）呢，也是其中我们需要思考的。
• 缺点：样本不平衡时即一类样本数量远远多于另一类样本，导致虽然离样本距离小的训练样本少，但大容量类的样本占据较大的数量时会导致分类错误。

2、距离度量

• 距离度量主要有三种计算方法：欧氏距离、曼哈顿距离和切比雪夫距离。

• 特征空间中两个实例间的距离是两个实例点相似程度的反映。一般情况下，我们使用的都是欧式距离，但也可以是其他距离，例如更一班的$L_p$距离或者Minkowski距离。前提要进行归一化。

• 设特征空间$\chi$是n维实数向量空间$R^n$，$x_i,x_j\in \chi$,$x_m=(x_i^{(1)},x_i^{(2)},\dots x_i^{(n)}{)}^T,m=i,j$ ，则$x_i，x_j$的$L_p$距离为：
  $$L_p(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^p{)}^{\frac{1}{p}},p>=1$$

• 当p = 1 时，则为曼哈顿距离，即：
  $$L_1(x_i,x_j)=\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}|$$

• 当p = 2 时，则为欧氏距离，即：
  $$L_2(x_i,x_j)=(\sum _{l=1}^n|x_i^{(l)}-x_j^{(l)}{|}^2{)}^{\frac{1}{2}}$$

• 当p = $\infty$ 时，则为切比雪夫距离，即：
  $$L_{\infty }(x_i,x_j)=ma{x}_l|x_i^{(l)}-x_j^{(l)}|$$

3、K值的选取

• k值得选取会对k近邻得结果产生很大的影响。

• 如果k值很小，就相当于在很小的领域中训练实例进行预测，学习的“近似误差”会减小，只有与待分类实例较近（相似得）的训练实例才会对预测结果起到作用，但缺点是学习的估计误差会增大，若邻近实例恰好是噪声，则预测结果肯定是错误得，容易产生过拟合；

• 如果k值较大，就相当于在较大的领域中训练实例进行预测，优点是减小学习的估计误差，这时与待分类实例较远的训练实例（不相似得）也会对预测结果起到作用，是预测结果发生错误。

• 如果K=N，则无论输入什么实例，那么改实例得类别都是训练数据集中数据最多的那个类别，模型过于简单，完全忽略了训练实例中得大量有用信息，不可取。

• 在应用中，通常会取一个较小的值，采用交叉验证选取最优K值。

• 近似误差：对现有训练集的训练误差，关注训练集，如果近似误差过小可能会出现过拟合的现象，对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。

• 估计误差：可以理解为对测试集的测试误差，关注测试集，估计误差小说明对未知数据的预测能力好，模型本身最接近最佳模型。

二、python实战

1、回归

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
np.random.seed(0)

# 随机生成40个(0, 1)之前的数，乘以5，再进行升序  作为特征x 一维的 方便可视化
X = np.sort(5 * np.random.rand(40, 1), axis=0)
# 创建[0, 5]之间的500个数的等差数列, 作为回归后的测试数据  画出回归线
T = np.linspace(0, 5, 500)[:, np.newaxis]
# 使用sin函数得到y值，并拉伸到一维  (X,y) 形成训练集 
y = np.sin(X).ravel()
# y值增加噪声
y[::5] += 1 * (0.5 - np.random.rand(8))

# 设置多个k近邻进行比较
n_neighbors = [1, 3, 5, 8, 10, 40]
# 设置图片大小
plt.figure(figsize=(18,8))
for i, k in enumerate(n_neighbors):
    # 欧氏距离p=2
    clf = KNeighborsRegressor(n_neighbors=k, p=2, metric="minkowski")
    # 训练
    clf.fit(X, y)
    # 预测
    y_ = clf.predict(T)
    plt.subplot(2, 3, i + 1)
    plt.scatter(X, y, color='red', label='train_data')
    plt.plot(T, y_, color='blue', label='pre_data')
    plt.axis('tight')
    plt.legend()
    plt.title("KNeighborsRegressor (k = %i)" % (k))

plt.tight_layout()
plt.show()

• 从图可以看出：k=1的时候，每个训练数据均在回归线上，此时形成了过拟合；而当k=40的时候，仅有一点点数据在回归线上，无论测试集x为多少数值，它的y值是定值，此时形成欠拟合，训练无意义。k = 5或者k=8的时候拟合效果好像还是不错的。

2、分类

• sklearn自带数据集：手写体预测

2.1、K值的确定

from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split,validation_curve
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler

plt.rcParams['font.sans-serif'] =['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

digits = load_digits()

X = digits['data'][:,:2]  # 取数据前两个特征 方便可视化
Y = digits['target']      # 标签

# 分割训练集和测试集 
X_train, X_test, y_train, y_test = train_test_split(X,Y,random_state= 0,test_size=0.3) 

# 数据标准化
X_train = StandardScaler().fit_transform(X_train)
X_test = StandardScaler().fit_transform(X_test)

# 价差验证精度得分
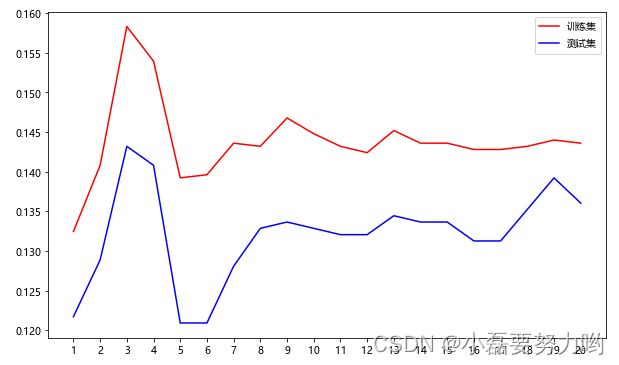
train_scores, test_scores = validation_curve(
                                            KNeighborsClassifier(),  # KNN算法
                                            X_train, y_train, cv=3, # 输入训练集 且划分为子训练集和子测试集 7:3
                                            param_name='n_neighbors', #
                                            param_range=range(1, 21), # 训练50次
                                            scoring='accuracy')

train_scores_mean = np.mean(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)

plt.figure(figsize=(10,6))
plt.plot(np.arange(1,21).astype(dtype=np.str),train_scores_mean,color='red',label='训练集')
plt.plot(np.arange(1,21).astype(dtype=np.str),test_scores_mean,color='blue',label='测试集')
plt.legend()
plt.show()

• K值选择3较好。此时训练集和测试集精度相比较来说较高。

2.2、分类

from sklearn.metrics import accuracy_score
knn = KNeighborsClassifier(n_neighbors=3,p=2,metric="minkowski")
knn.fit(X_train, y_train)
y_pre= knn.predict(X_test)
print(accuracy_score(y_test, y_pre)) # 0.1074074074074074
#或者print(knn.score(X_test,y_test))
print(knn.predict([[0.3,0.4],[7.8,-9.1],[12.9,43.2]))  # [2 0 5]
# 特征为[0.3,0.4],[7.8,-9.1],[12.9,43.2] 的手写体分别为 2 0 5 

参考：
近似误差与估计误差参考于 K-近邻算法的超参数K值以及取值问题
《统计学习方法 李航著》