【机器学习系列】【模型评价】【ROC曲线、约登指数最佳阈值】一个函数中实现约登指数计算并集成到ROC图中,给出默认阈值及最佳阈值下的混淆矩阵
输入实际标签、预测的概率值、预测标签,计算最佳阈值,输出ROC曲线,输出默认阈值下的混淆矩阵和最佳阈值下的混淆矩阵
目录
使用约登指数计算最佳阈值
result_evaluation()函数实现约登指数计算并集成到ROC图中,给出默认阈值及最佳阈值下的混淆矩阵
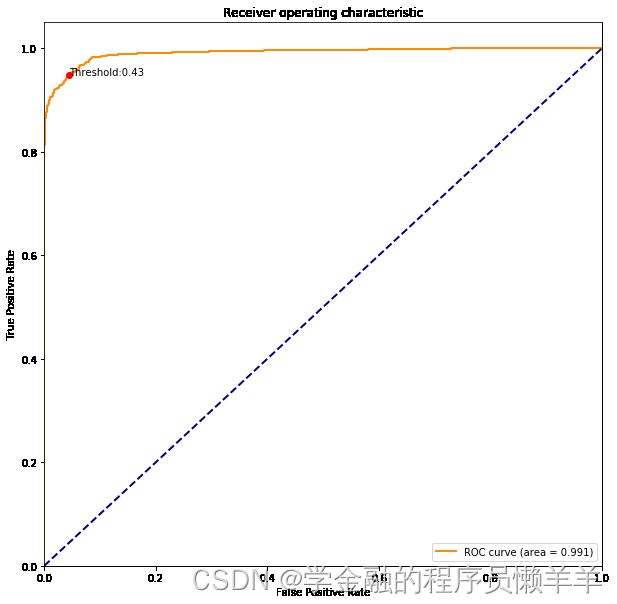
结果展示
使用约登指数计算最佳阈值
#最佳阈值点(使用约登指数)
def Find_Optimal_Cutoff(TPR, FPR, threshold):
y = TPR - FPR
Youden_index = np.argmax(y) # Only the first occurrence is returned.
optimal_threshold = threshold[Youden_index]
point = [FPR[Youden_index], TPR[Youden_index]]
return optimal_threshold, point
result_evaluation()函数实现约登指数计算并集成到ROC图中,给出默认阈值及最佳阈值下的混淆矩阵
#输出混淆矩阵、精确率、召回率、F1、均方误差和确定系数并画roc曲线函数
def result_evaluation(y,prob,pred):
"""
输入实际标签、预测的概率值、预测标签,计算最佳阈值,输出ROC曲线,输出默认阈值下的混淆矩阵和最佳阈值下的混淆矩阵
Parameters:
y - 实际标签(测试集的y)
prob - 模型预测的概率值(estimtor.predict_proba()的返回值)
pred - 模型预测值(estimtor.predict()的返回值)
注:参数数据类型为array
Returns:
无
Raises:
KeyError - raises an exception
"""
# if(type(prob)!='array'):
# prob = np.array(prob)
# #print(prob)
fpr,tpr,threshold = roc_curve(y,prob[:,1]) ###计算真正率和假正率
roc_auc = auc(fpr,tpr) ###计算auc的值
optimal_th, optimal_point = Find_Optimal_Cutoff(TPR=tpr, FPR=fpr, threshold=threshold)
plt.figure()
lw = 2
plt.figure(figsize=(10,10))
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve (area = %0.3f)' % roc_auc) ###假正率为横坐标,真正率为纵坐标做曲线
plt.plot(optimal_point[0], optimal_point[1], marker='o', color='r')
plt.text(optimal_point[0], optimal_point[1], f'Threshold:{optimal_th:.2f}')
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic')
plt.legend(loc="lower right")
#TN|FP
#FN|TP
#混淆矩阵
pred2 = (prob[:,1] >=optimal_th ).astype(bool)
print('最佳阈值下混淆矩阵:')
print(confusion_matrix(y,pred2))
accuracy = accuracy_score(y, pred2)
print("准确率:",accuracy)
pre = metrics.precision_score(y, pred2)
print("精确率:",pre)
print("召回率:",metrics.recall_score(y, pred2))
print("F1",metrics.f1_score(y, pred2))
print("均方误差",mean_squared_error(y, pred2))
print("确定系数",r2_score(y, pred2))
print("*****************************************")
print("*****************************************")
print('非最佳阈值下混淆矩阵:')
print(confusion_matrix(y,pred))
accuracy = accuracy_score(y, pred)
print("准确率:",accuracy)
pre = metrics.precision_score(y, pred)
print("精确率:",pre)
print("召回率:",metrics.recall_score(y, pred))
print("F1",metrics.f1_score(y, pred))
print("均方误差",mean_squared_error(y, pred))
print("确定系数",r2_score(y, pred))
plt.show()结果展示
最佳阈值下混淆矩阵: [[3497 161] [ 189 3469]] 准确率: 0.952159650082012 精确率: 0.9556473829201102 召回率: 0.948332422088573 F1 0.9519758507135017 均方误差 0.047840349917987975 确定系数 0.8086386003280481 ***************************************** ***************************************** 非最佳阈值下混淆矩阵: [[3558 100] [ 270 3388]] 准确率: 0.9494259158009841 精确率: 0.9713302752293578 召回率: 0.9261891744122471 F1 0.9482227819759306 均方误差 0.05057408419901586 确定系数 0.7977036632039366