matlab:圆内均匀随机取点
文章目录
-
- 1.舍选法
- 2.反函数法
- 3.代码
这里介绍两种圆内均匀取点的方法:舍选法和反函数法。
1.舍选法
顾名思义,舍选法是指在正方形(边长等于圆直径)的上面均匀撒点,然后在正方形上画圆,超出圆形的舍弃掉,只保留圆内的点:
效果如下

2.反函数法
一般取某个概率密度函数下的随机数,会用到反函数法,这里的反函数指的是累积分布函数的反函数。如图所示,纵轴为概率,横轴为随机数的取值,可以看到在纵轴区间相等的间隔内,横轴不同的随机数被取到的概率是不同的,但是相同间隔内的概率是相等的,也就是说纵轴的随机数是均匀的,当我们在按照均匀分布在纵轴上随机取(0,1)区间中的随机数的时候,会对应到的累积分布函数的横坐标的值,而这个过程即是取某个概率密度函数下的随机数的过程。对于上述的理解至关重要,较好的理解方式是等纵轴间隔下对应横坐标的某区间,而这个区间被取到的概率就是对应的纵轴的区间概率值的大小。
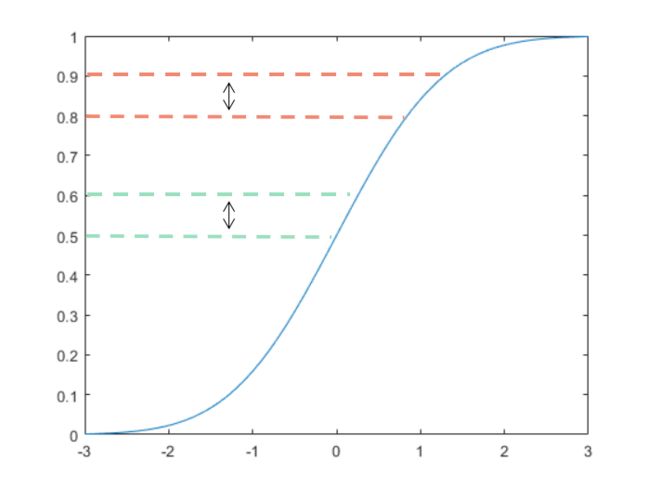
在此处的问题中,随机点要在圆内均匀分布,按照字面上理解,意思应该是每单位的面积点的数量要相同,即数量要和面积呈正比。那么,接下来的工作就是找到在半径R上的点的分布密度。

上图为圆的一部分,是一个扇形,张角即为 θ \theta θ,由圆心O到A的距离为 r 0 r_{0} r0,由A到B的距离为 Δ r \Delta r Δr,那么我想计算AB这段对应的面积,应该有如下公式计算得出:
S 0 = π ( r 0 + Δ r ) 2 θ 2 π − π r 0 2 θ 2 π = θ 2 ( 2 r 0 Δ r + Δ r 2 ) \begin{aligned} S_{0}&=\frac{\pi(r_{0}+\Delta r)^{2}\theta}{2\pi}-\frac{\pi r_{0}^{2}\theta}{2\pi}\\ &=\frac{\theta}{2}(2r_{0}\Delta r+\Delta r^{2}) \end{aligned} S0=2ππ(r0+Δr)2θ−2ππr02θ=2θ(2r0Δr+Δr2)
相应的,在R上取另一段长度记为 r 1 r_{1} r1,也有对应在 r 1 r_{1} r1处的面积。
S 1 = π ( r 1 + Δ r ) 2 θ 2 π − π r 1 2 θ 2 π = θ 2 ( 2 r 1 Δ r + Δ r 2 ) \begin{aligned} S_{1}&=\frac{\pi(r_{1}+\Delta r)^{2}\theta}{2\pi}-\frac{\pi r_{1}^{2}\theta}{2\pi}\\ &=\frac{\theta}{2}(2r_{1}\Delta r+\Delta r^{2}) \end{aligned} S1=2ππ(r1+Δr)2θ−2ππr12θ=2θ(2r1Δr+Δr2)
下面计算二者的比值:
lim Δ r → 0 S 0 S 1 = r 0 r 1 \lim_{\Delta r \rightarrow 0}\frac{S_{0}}{S_{1}}=\frac{r_{0}}{r_{1}} Δr→0limS1S0=r1r0
很明显位于 r 0 r_{0} r0和 r 1 r_{1} r1处的扇形面积正比于半径之比。
因此可以断定,点的密度应当正比于取的r。因此在半径R上的随机函数,其概率密度函数 f f f应当满足于如下条件:
f ( r 0 ) f ( r 1 ) = r 0 r 1 \frac{f(r_{0})}{f(r_{1})}=\frac{r_{0}}{r_{1}} f(r1)f(r0)=r1r0
这里很好理解,既然点的数量正比于 r r r,这也就是说其概率密度正比于 r r r。
因此我们构造概率密度函数:
f ( x ) = k x f(x)=kx f(x)=kx
其函数图像长这个样子:

其中, x x x的取值范围就为 [ 0 , R ] [0,R] [0,R]。但 k k k还不确定,所以要首先确定 k k k的值。
根据概率密度函数的要求,其积分结果等于1:
∫ 0 R k x d x = 1 2 k x 2 ∣ 0 R = 1 2 k R 2 = 1 \int_{0}^{R}kxdx=\frac{1}{2}kx^{2}|_{0}^{R}=\frac{1}{2}kR^{2}=1 ∫0Rkxdx=21kx2∣0R=21kR2=1
得出:
k = 2 R 2 k=\frac{2}{R^{2}} k=R22
由此,得到累积概率分布函数 F ( x ) F(x) F(x)的完整形式:
F ( x ) = ∫ 2 R 2 x d x = 2 R 2 ( 1 2 x 2 + C ) F(x)=\int \frac{2}{R^{2}}xdx=\frac{2}{R^{2}}(\frac{1}{2}x^{2}+C) F(x)=∫R22xdx=R22(21x2+C)
当 x = 0 x=0 x=0时,累积分布 F ( x ) F(x) F(x)应当为0,当 x = R x=R x=R时,累积概率分布 F ( x ) F(x) F(x)应当为1,。由此得出 C = 0 C=0 C=0,即累积概率分布函数最终版本为:
F ( x ) = 1 R 2 x 2 F(x)=\frac{1}{R^{2}}x^{2} F(x)=R21x2
由上式可以获得反函数:
F − 1 ( x ) = R x F^{-1}(x)=R\sqrt{x} F−1(x)=Rx
根据反函数法, x x x为[0,1]均匀分布的随机数时,符合概率密度函数 f ( x ) f(x) f(x)的分布。最终,我们就找到了这个随机数发生器。
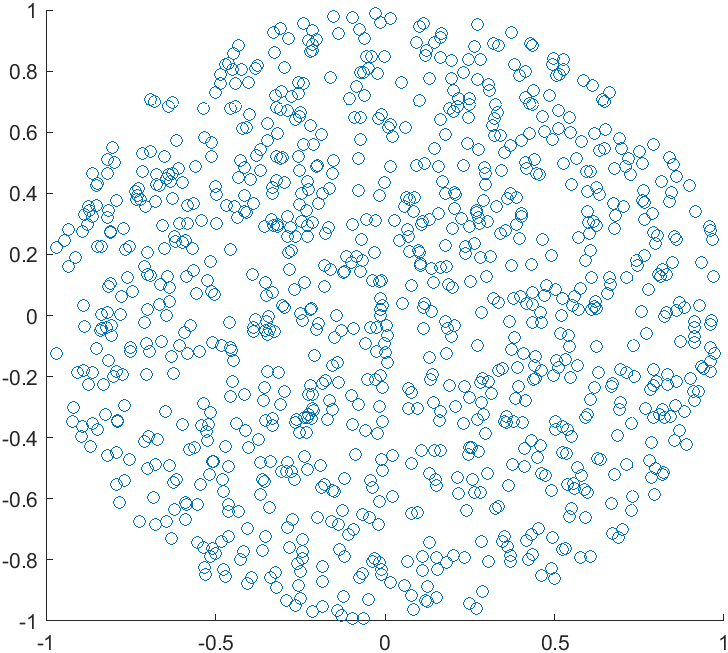
效果如下:
当然上述的推导是从概率密度函数间接得出累积概率分布函数,其实我们也可以从另一个角度解释下图,从而直接得出累积概率分布函数的公式:

当我们取 r 0 r_{0} r0时,其相应的扇形面积为:
S 0 = π r 0 2 θ 2 π \begin{aligned} S_{0}&=\frac{\pi r_{0}^{2}\theta}{2\pi}\\ \end{aligned} S0=2ππr02θ
注意到半径所对应的面积会随半径的平方成正比,而这个面积其实与累积概率分布函数值成正比,即面积越大,点数量越多,概率越大。
所以累积概率分布函数形式应该为:
F ( x ) = g x 2 F(x)=gx^{2} F(x)=gx2
当 x = R x=R x=R时, F ( x ) F(x) F(x)应当取最大值1,代入到上式中得到:
g = 1 R 2 g=\frac{1}{R^{2}} g=R21
所以累积分布函数为:
F ( x ) = 1 R 2 x 2 F(x)=\frac{1}{R^{2}}x^{2} F(x)=R21x2
这个结果与前一种间接方法一样。
比较取1000点时,两种方法在matlab中所用时间:
%舍选法
\>> TestRandCircle
历时 0.001868 秒。
%反函数法
\>> TestRandCircle
历时 0.001485 秒。
所以反函数法在matlab中的取点速度要比舍选法更高。
3.代码
%matlab
%取圆内的随机数;
xy=zeros(1000,2);
tic
for i=1:1:1000
[xy(i,1),xy(i,2)]=RandCircle(1); %注意要分开赋值!!
end
toc
scatter(xy(:,1),xy(:,2));
%反函数法
function [x,y]=RandCircle(radius)
rand_theta=rand()*pi*2;
rand_radius=sqrt(rand())*radius;
x=cos(rand_theta)*rand_radius;
y=sin(rand_theta)*rand_radius;
end
%%舍选法
% function [x,y]=RandCircle(radius)
% while 1
% x=(rand()-0.5)*2*radius;
% y=(rand()-0.5)*2*radius;
% if (x^2+y^2)相关资料:
在圆中均匀分布随机点