时间复杂度和空间复杂度

算法的时间复杂度和空间复杂度

首先我们先了解什么是算法，算法（Algorithm）是指用来操作数据、解决程序中的问题的方法
如果我们有一个问题，用不同的算法去解决，结果可能是一样的，但是中间消耗的时间和空间一定是不一样的
算法分析有二种：第一种是时间的效率，第二种是空间的效率

什么是时间复杂度

算法的基本操作的执行次数，为算法的时间复杂度
时间复杂度是指程序要运算多少次，这个算法所需要的计算工作量
测试一个程序的执行时间通常有两种方法**

事后统计法

一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道
这方法可以但是有二个缺点：
一 是必须在计算器上实际测试
二 是所得时间的统计量依赖于计算机的硬件、软件等环境因素，有时容易掩盖算法本身的优势

事前分析估算

在编写程序前，依据统计方法对算法进行估算（大概的运行次数）
一个程序在计算机上运行时所消耗的时间取决于下列因素：

1. 算法采用的策略方法
2. 编译产生的代码质量
3. 问题的输入规模
4. 机器执行指令的速度

计算常见的时间复杂度

实际练习

例题1：

请计算一下Fun执行了几次呢？
void Fun(int n)
{
	int count = 0;
	for (int i = 0; i < n; i++)//count在这里执行了N*N次。
	{
		for (int j = 0; j < n; j++)
		{
			count++;
		}
	}
	for (int i = 0; i < 2 * n; i++)//在这里执行了2*N次。
	{
		count++;
	}
	for (int i = 0; i < 10; i++)//在这里执行了10次。
	{
		count++;
	}
}

准确的次数是：N²+2N+10次
在这里我们只统计了主要的执行次数。然而时间复杂度其实是一种估算，是由影响时间复杂度最大项决定的，在这里影响最大的项为N²
Fun执行的次数：

N的值	N²的值	计算的次数
10	100	130
100	10000	10210
1000	1000000	1002010

随N值的增大，这个表达式 N²对结果的影响是最大的
时间复杂度是估算，是看表达式中影响最大的那一项
我们计算时间复杂度时，其实并不一定要计算精确的次数，而只需要大概的执行次数，这里我们使用大O的渐进法
大O符号：适用于描述函数中渐进行为的表示法
推导大O阶的方法方法：

1. 用常数1代替式中所有常数。
2. 在修改过的式子中保留最高阶。
3. 若最高阶为常数结果就是1。
4. 若最高阶不是常数的话结果就是这个最高阶

例子 1：

计算Fun的时间复杂度
void Fun(int N)
{
	int count = 0;
	for (int K = 0; K < 2 * N; K++)//执行2N次
	{
		count++;
	}
	int M = 0;
	for (M = 10; M > 0; M--)//执行10次
	{
		count++;
	}
	printf("%d\n", count);
}

准确次数：2*N+10
答案是：O(N)
O（）表示是估算

例子2：

计算Fun2的时间复杂度
void Fun2(int N, int M)
{
    int count = 0;
    for (int k = 0; k < N; k++) 执行次数为N
    {
        const++;
    }
    for (int k = 0; k < M; k++) 执行次数为M
    {
        const++;
    }
}

答案是：O(N+M)

是因为我们不知道N和M的大小，N和M都是未知数，注意时间复杂度里不可能只有一个未知数，有可能有多个未知数

假设：题中说M远远大于N，
那么答案就是：O(M)

假设：M和N差不多大，
那答案是：O(M) 或 O(N)，可以理解成二倍N或者 二倍M

例子3：

计算Fun3的时间复杂度
void Fun3(int N)  这里的N对我们的时间复杂度没有影响
{
    int count = 0;
    for (int k = 0; k < 100; k++)  在此处执行了100次
    {
        count++;
    }
    printf("%d\n", count);
}

答案：O(1)

1. 用常数1代替式中所有常数

意思是只要是常量，都用1去替代
无论是10，还是100，只要是常数，都是O(1)
确定的常数次(常量)，都是O(1)

例子4：

在 char* str的字符串里找，rac需要的字符，找到了就返回

计算Fun4的时间复杂度
const char* strch(const char* str, char rac)
{
    while (*str != '\0')   这里str是字符串
    {
        if (*str == rac)
        {
            return str;
        }
        str++;
    }
    return NULL;
}

假设在长度为N的字符串，找字符‘a’ ，一进来就找到了
那字符‘e’呢，要找到第五个字符才能找到
字符‘x’呢，找遍整个字符都找不到

这就要分情况了
有些算法的时间复杂度存在最好、平均和最坏的情况
最坏情况：操作执行的最大次数（上界）
平均情况：操作执行的期望运行次数
最好情况：操作执行的最小次数
例如：在长度为N的字符串，找字符‘a’
最好的情况：1次找到
平均的情况：N/2次找到
最坏的情况：N次找到

在实际中一般情况关注的是最坏的情况，所以答案是：O(N)

例子5：

计算这个冒泡排序的时间复杂度
void bubble(int* str,int sz)
{
	int i = 0;
	for (i = 0; i < sz-1; i++)
	{
		int j = 0;
		for (j = 0; j < sz - 1 - i; j++)
		{
			if (str[j] > str[j + 1])
			{
				int tmp = str[j];
				str[j] = str[j + 1];
				str[j + 1] = tmp;
			}
		}
	}
}

看下面动态图，方便理解冒泡排序

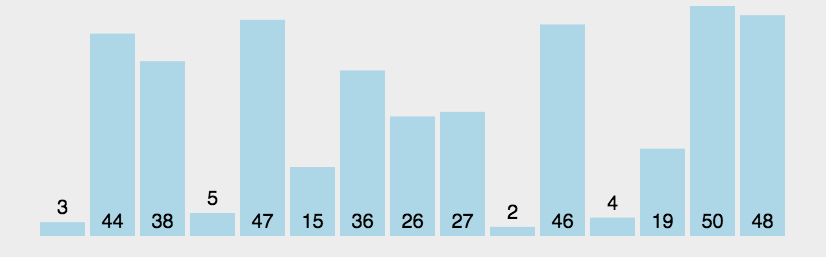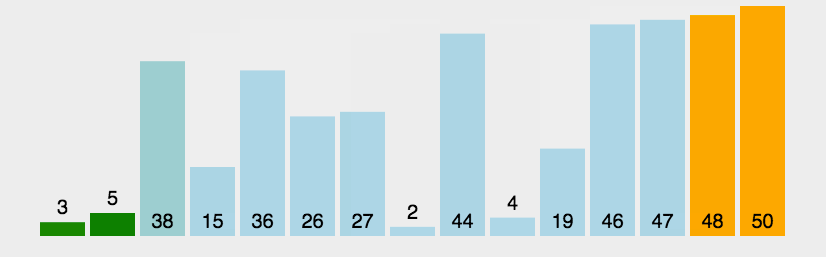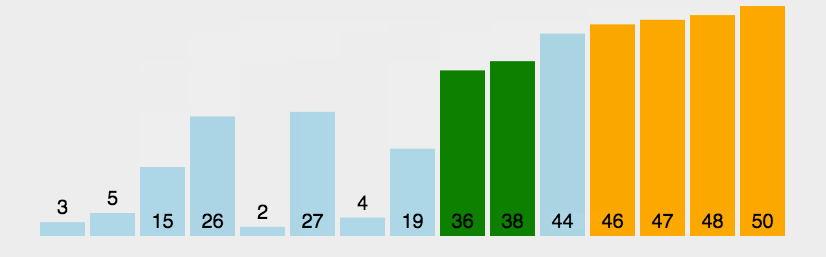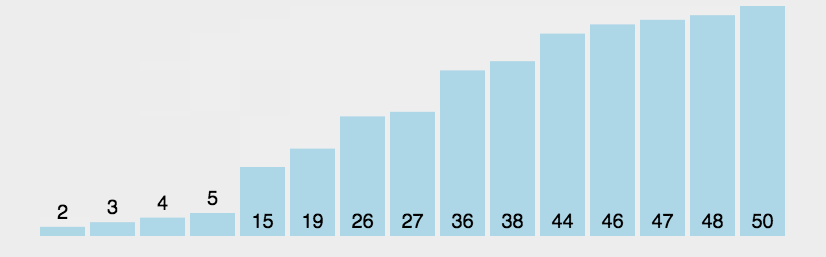
第一趟冒泡：N次
第二趟冒泡：N-1次
第三趟冒泡：N-2次
…
第N趟：1次
准确的次数是：（N+1）*N/2
答案：O（N²）

例子6：

这个例子是二分查找

计算Fun6的时间复杂度
int Binary(int* a, int n, int x)
{
    int left = 0;
    int right = n;
    while (left < right)
    {
        int mid = left + (right - left) / 2;
        if (a[mid] < x)
            left = mid + 1;
        else if (a[mid] > x)
            right = mid;
        else
            return mid;
    }
    return -1;
}

假设找了X次
1*.2*.2*.2…*2 = N
2^x = N
x = logN
答案是：O(logN)

例子7：

计算Fun7的时间复杂度
计算阶乘的递归
long long Fac(int N)
{
   return N < 2 ？ N : Fun(n-1)*N;
   }

它递归了N次，每次递归运算 O（1）
整体就是:O(N)

时间的复杂度对比

常见的时间复杂度：
O(N^2)、O(N)、O(logN)、O(1)

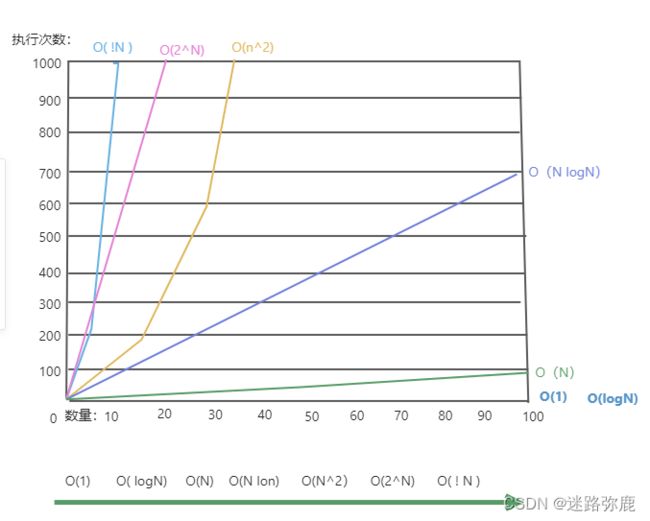
空间复杂度

空间复杂度是计算算法所耗费的存储空间。
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度，同样反映的是一个趋势，我们用 S(n) 来定义。
空间复杂度比较常用的有：O(1)、O(n)、O(n²)，我们下面来看看：

例子1：

int i = 1;
int j = 2;
++i;
j++;
int m = i + j;

代码中的 i、j、m 所分配的空间都不随着处理数据量变化，因此它的空间复杂度 S(n) = O(1)

例子2：

int[] m = new int[n]
for(i=1; i<=n; ++i)
{
   j = i;
   j++;
}

这段代码中，第一行new了一个数组出来，这个数据占用的大小为n，这段代码的2-6行，虽然有循环，但没有再分配新的空间，因此，这段代码的空间复杂度主要看第一行即可，即 S(n) = O(n)