【算法刷题】——力扣第77场双周赛
力扣第77场双周赛
- 一、统计是给定字符串前缀的字符串数目
-
- ️1.题目描述
- ️2.题目分析
- ️3.代码实现
- 二、最小平均差
-
- ️1.题目描述
- ️2.题目分析
- ️3.代码实现
- 三、统计网格中没有被保卫的格子数
-
- ️1.题目描述
- ️2.题目分析
- ️3.代码实现
一、统计是给定字符串前缀的字符串数目
原题传送门
️1.题目描述
给你一个字符串数组 words 和一个字符串 s ,其中 words[i] 和 s 只包含 小写英文字母 。
请你返回 words 中是字符串 s 前缀 的 字符串数目 。
一个字符串的 前缀 是出现在字符串开头的子字符串。子字符串 是一个字符串中的连续一段字符序列。
示例:
输入:
words = [“a”,“b”,“c”,“ab”,“bc”,“abc”], s = “abc”
输出:
3
说明:
words 中是 s = “abc” 前缀的字符串为: “a” ,“ab” 和 “abc” 。
所以 words 中是字符串 s 前缀的字符串数目为 3 。
️2.题目分析
想着第一题简单,看完一遍题目看了下示例就直接写代码了。仅比较了每个字符串的第一个字符,啪一下很快啊,WA
果然,wa一下就老实了,认真看了下题目,匹配前缀,需要字符数组中每个字符串的每一个字符都与给定字符串进行匹配,如果成功就是前缀
(注意:给定字符串的长度需要满足 ≥ 字符数组中每个字符串的长度)
️3.代码实现
class Solution {
public int countPrefixes(String[] words, String s) {
int count = 0;
for(String s1 : words){
//如果s长度 小于 s1长度 一定不是前缀
if(s.length() < s1.length()) continue;
int len = s1.length();
boolean flag = true;
for(int i = 0;i < len;i++){
//如果有一个不相等的就结束比较
if(s.charAt(i) != s1.charAt(i)){
flag = false;
break;
}
}
if(flag) count++;
}
return count;
}
}
二、最小平均差
原题传送门
️1.题目描述
给你一个下标从 0 开始长度为 n 的整数数组 nums 。
下标 i 处的 平均差 指的是 nums 中 前 i + 1 个元素平均值和 后 n - i - 1 个元素平均值的 绝对差 两个平均值都需要 向下取整 到最近的整数。
请你返回产生 最小平均差 的下标。如果有多个下标最小平均差相等,请你返回 最小 的一个下标。
注意:两个数的 绝对差 是两者差的绝对值。 n 个元素的平均值是 n 个元素之 和 除以(整数除法)n 。 0 个元素的平均值视为 0 。
示例 1:
输入: nums = [2,5,3,9,5,3]
输出: 3
解释:
- 下标 0 处的平均差为:|2 / 1 - (5 + 3 + 9 + 5 + 3) / 5| = |2 / 1 - 25 / 5| = |2 - 5| = 3 。
- 下标 1 处的平均差为:|(2 + 5) / 2 - (3 + 9 + 5 + 3) / 4| = |7 / 2 - 20 / 4| = |3 - 5| = 2 。
- 下标 2 处的平均差为:|(2 + 5 + 3) / 3 - (9 + 5 + 3) / 3| = |10 / 3 - 17 / 3| = |3 - 5| = 2 。
- 下标 3 处的平均差为:|(2 + 5 + 3 + 9) / 4 - (5 + 3) / 2| = |19 / 4 - 8 / 2| = |4 - 4| = 0 。
- 下标 4 处的平均差为:|(2 + 5 + 3 + 9 + 5) / 5 - 3 / 1| = |24 / 5 - 3 / 1| = |4 - 3| = 1 。
- 下标 5 处的平均差为:|(2 + 5 + 3 + 9 + 5 + 3) / 6 - 0| = |27 / 6 - 0| = |4 - 0| = 4 。
下标 3 处的平均差为最小平均差,所以返回 3 。
提示:
1 <= nums.length <= 1050 <= nums[i] <= 105
️2.题目分析
题目意思就是求解nums数组,前 i+1 个元素的平均值 与 后 n-i-1 个元素的平均值 之差的绝对值的 最小值的位置下标 i
吸取第一题的教训理解题目意思后,才开始写代码,上来就是一个暴力双循环,啪一下很快啊,WA 果然还是老老实实想其他方法吧
因为每次都是从 下标 i 进行分隔,前面的i+1 个的元素和 与后面的元素和 两者相加就是nums数组的元素和,因此,后面元素的和 = 数组和 - 前面元素的和
- 求nums数组元素和 count
- 从前往后遍历数组 另设一个变量 sum 每次加上遍历的元素
- 后面元素的和就是 count - sum
- 求前后两个元素和的平均值 并求绝对值的差
- 比较更新最小值下标
(注意:n-i-1可能为 0 这个时候 就不能 作分母了。 求和数据是可能超过int类型的,因为选择long类型的变量记录和)
️3.代码实现
class Solution {
public int minimumAverageDifference(int[] nums) {
int n = nums.length;
int min = Integer.MAX_VALUE;
int idx = -1;
long count = 0;
long sum = 0;
//求和
for(int i = 0 ; i < n;i++) count+=nums[i];
for(int i = 0; i < n;i++){
// 前 i + 1个元素的和
sum += nums[i];
//求平均值
long l = sum/(i+1);
long r = 0;
//考虑 n-1-i等于0的情况
if(i!= n-1) {
r = (count - sum) / (n - i - 1);
}
//求差值的绝对值 并更新
int num = (int) Math.abs(l-r);
if(num < min){
min = num;
idx = i;
}
}
return idx;
}
}
三、统计网格中没有被保卫的格子数
原题传送门
️1.题目描述
给你两个整数
m和n表示一个下标从 0 开始的m x n网格图。同时给你两个二维整数数组guards和walls,其中guards[i] = [rowi, coli]且walls[j] = [rowj, colj],分别表示第 i 个警卫和第 j 座墙所在的位置。
一个警卫能看到 4 个坐标轴方向(即东、南、西、北)的 所有 格子,除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被 至少 一个警卫看到,那么我们说这个格子被 保卫 了。
请你返回空格子中,有多少个格子是 没被保卫 的。
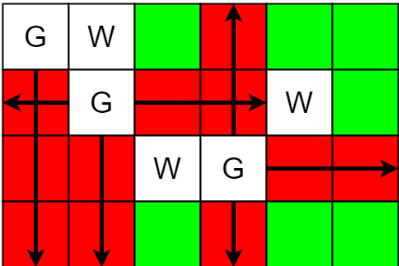
输入: m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]
输出: 7
解释: 上图中,被保卫和没有被保卫的格子分别用红色和绿色表示。 总共有 7 个没有被保卫的格子,所以我们返回 7 。
提示:
1 <= m, n <= 10^52 <= m * n <= 10^51 <= guards.length, walls.length <= 5 * 10^42 <= guards.length + walls.length <= m * nguards[i].length == walls[j].length == 20 <= rowi, rowj < m0 <= coli, colj < nguards 和 walls 中所有位置 互不相同 。
️2.题目分析
根据题目描述,首先想到了是DFS,由于周赛时间是晚上10点半 —— 12点,写到这里就已经11点了,太晚了,要回宿舍睡大觉了…
第二天以dfs的思路写着写着就写不下去了,主要是怎么如何只进行四个方向的持续遍历,如果使用dfs会以每个格子为起点进行上下左右遍历,但是题目意思显然是 仅朝着四个方向,看了题解区大佬的解法,使用方向数组可以解决这个问题了。
- 初始化一个 m x n 的数组res 数组值 -1表示墙 1表示守卫 2表示被保护 0表示没有被保护
- 将墙和守卫的位置对res数组进行状态更新
- 遍历每个守卫,使用方向数组,并不断进行四个方向遍历 直至遇到墙或者其他守卫 或者超过res数组边界 并将保卫的地方更新数组值为 2
- 遍历数组res 统计0的个数 就是所求
️3.代码实现
class Solution {
int[][] res;
public int countUnguarded(int m, int n, int[][] guards, int[][] walls) {
res = new int[m][n];
// -1表示墙 1表示守卫 2表示被保护 0表示没有被保护
for (int[] guard : guards) {
res[guard[0]][guard[1]] = 1;
}
for (int[] wall : walls) {
res[wall[0]][wall[1]] = -1;
}
//定义一个方向数组
int[][] dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
//从每个守卫出发遍历四个方向 标记被保护的位置
for (int[] guard : guards) {
int x = guard[0];
int y = guard[1];
for (int i = 0; i < 4; i++) {
int nx = x + dir[i][0], ny = y + dir[i][1];
//检查 nx ny 是否合法 并且 不能被墙或者守卫挡着
while (nx >= 0 && ny >= 0 && nx < m && ny < n && res[nx][ny] != -1 && res[nx][ny] != 1) {
res[nx][ny] = 2;
//关键 保证只是向四个方向扩散
nx += dir[i][0];
ny += dir[i][1];
}
}
}
int ans = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (res[i][j] == 0) ans++;
}
}
return ans;
}
}
就先分析前三题吧,第四题再想想