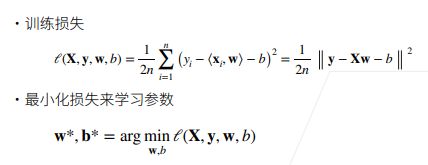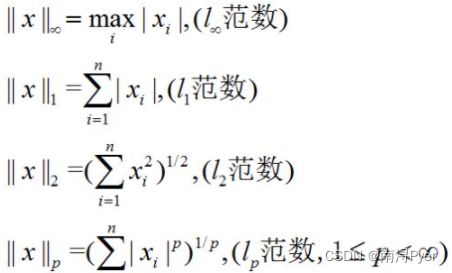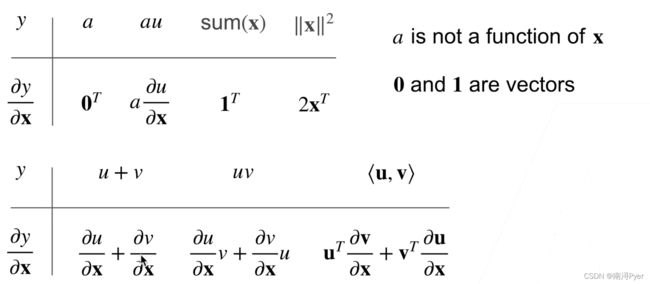【动手学深度学习v2笔记】线性回归 + 基础优化算法

1 线性回归

1.1 一个简单模型

1.2 线性模型

![在这里插入图片描述](https://img-blog.csdnimg.cn/8c8da08b92db46a4af6d4581ba361d8a.png

上图将权重层和输入层看成一层，输入层各权重均为1。

1.3 平方损失

1.4 训练数据

1.5 损失函数

argmin()函数是求当损失函数最小的时候的参数值。

1.6 显式解

方程的解可以写出y=f(x)的叫显式解，要求解的未知量单独放在方程的左边，右边均为已知的字母和常数。
只能写出f(x,y)=C的叫隐式解，即要求解的未知量没有单独的拿出来放在方程的一边，方程往往是比较复杂的。

矩阵转置

范数求导

2 基础优化算法

2.1 梯度下降

当模型没有显示解时：

梯度：使得函数值增加最快的方向
梯度下降：使得函数值下降最快的方向
学习率：代表沿梯度下降的方向走多远

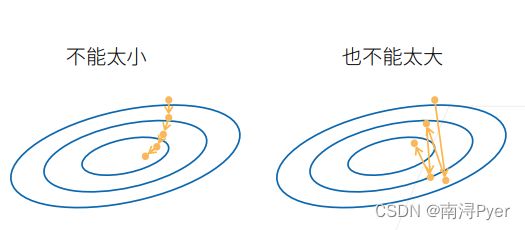
2.2 选择学习率

学习率太小：计算梯度次数太多，消耗资源大。
学习率太大：会导致震荡

2.3 小批量随机梯度下降

2.4 选择批量大小

3 线性回归的从零开始实现

%matplotlib inline
import random
import torch
from d2l import torch as d2l

%matplotlib inline这一句是IPython的魔法函数，可以在IPython编译器里直接使用，作用是内嵌画图，省略掉plt.show()这一步，直接显示图像。 如果不加这一句的话，我们在画图结束之后需要加上plt.show()才可以显示图像。

3.1 生成数据集

def synthetic_data(w, b, num_examples):  #@save
    """生成 y = Xw + b + 噪声。"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b 
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
# features中的每一行都包含一个二维数据样本
# labels中的每一行都包含一维标签值（一个标量）
features, labels = synthetic_data(true_w, true_b, 1000)

X为一个矩阵，行数表示有多少个样本，列数表示有多少个features

torch.normal(means, std, out=None)

返回一个张量，包含从给定参数means，std的离散正态分布中抽取随机数。
均值means是一个张量，包含每个输出元素相关的正态分布的均值。
标准差std是一个张量，包含每个输出元素相关的正态分布的标准差。
均值和标准差的形状不须匹配，但每个张量的元素个数须相同。
out (Tensor) – 可选的输出张量

torch.matmul(x, y)

当输入的矩阵x，y是都是二维时，就是普通的矩阵乘法

torch.reshape((-1, 1))

参数-1，表示模糊reshape的意思。
比如：reshape（-1,3），固定3列 多少行不知道。

print('features:', features[0],'\nlabel:', labels[0])

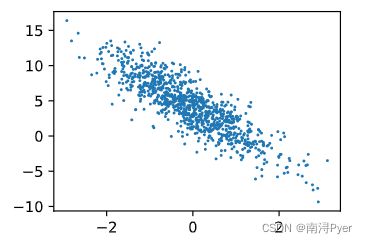
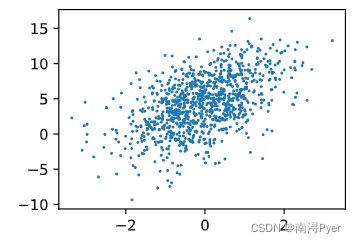
# W[1]<0，负相关
d2l.set_figsize()
# 绘制散点图 
# detach分离出数值，不再含有梯度
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);
# d2l.plt.show()

# W[0]>0，正相关
d2l.set_figsize()
d2l.plt.scatter(features[:, 0].detach().numpy(), labels.detach().numpy(), 1);
# d2l.plt.show() 

matplotlib.pyplot.scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, *, data=None, **kwargs)

x，y：表示的是大小为(n,)的numpy数组，即散点的坐标。
s：是一个实数或者是一个数组大小为(n,)，散点的面积。
c：散点的颜色（默认值为蓝色，‘b’）。
marker：散点样式（默认值为实心圆，‘o’）。
alpha：散点透明度（[0, 1]之间的数，0表示完全透明，1则表示完全不透明）。
linewidths：散点的边缘线宽。
edgecolors：散点的边缘颜色

3.2 读取数据集

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])
        # 二维张量的访问，torch中tensor的特性
        yield features[batch_indices], labels[batch_indices]

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

'''
tensor([[ 0.0285, -0.1467],
        [ 0.6119,  0.0424],
        [ 0.5622, -1.2591],
        [-0.2556,  2.8628],
        [-0.4648, -0.1241],
        [ 0.6994,  0.8691],
        [-0.6269, -0.2140],
        [ 0.2635, -1.6105],
        [-0.2415,  0.5402],
        [-0.6873, -0.9715]]) 
 tensor([[ 4.7522],
        [ 5.2650],
        [ 9.6032],
        [-6.0618],
        [ 3.7040],
        [ 2.6282],
        [ 3.6846],
        [10.1839],
        [ 1.8840],
        [ 6.1346]])
'''

yield 的作用就是把一个函数变成一个 generator，带有 yield 的函数不再是一个普通函数，Python 解释器会将其视为一个generator，调用 fab(5) 不会执行 fab 函数，而是返回一个 iterable 对象。
在 for循环执行时，每次循环都会执行 fab 函数内部的代码，执行到 yield b 时，fab 函数就返回一个迭代值，下次迭代时，代码从yield b 的下一条语句继续执行，而函数的本地变量看起来和上次中断执行前是完全一样的，于是函数继续执行，直到再次遇到 yield。
也可以手动调用 fab(5) 的 next() 方法（因为 fab(5) 是一个 generator 对象，该对象具有 next() 方法）

def fab(max): 
    n, a, b = 0, 0, 1 
    while n < max: 
        yield b      # 使用 yield
        # print b 
        a, b = b, a + b 
        n = n + 1
 
for n in fab(5): 
    print n
# 1 
# 1 
# 2 
# 3 
# 5

>>>f = fab(5) 
>>> f.next() 
1 
>>> f.next() 
1 
>>> f.next() 
2 
>>> f.next() 
3 
>>> f.next() 
5 
>>> f.next() 
Traceback (most recent call last): 
 File "", line 1, in <module> 
StopIteration

Python yield 使用浅析

3.3 初始化模型参数

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

3.4 定义模型

def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

3.5 定义损失函数

def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

3.6 定义优化算法

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

with torch.no_grad()
在使用pytorch时，并不是所有的操作都需要进行计算图的生成（计算过程的构建，以便梯度反向传播等操作）。而对于tensor的计算操作，默认是要进行计算图的构建的，在这种情况下，可以使用 with torch.no_grad():，强制之后的内容不进行计算图构建。
param.grad.zero_()
在默认情况下，PyTorch会累积梯度，我们需要清除之前的值,再一次调用sgd时就是下一个batch得到的param.grad，batch和batch是没有关系的。

pytorch中with torch.no_grad():
pytorch之object.grad.zero_()

3.7 训练

lr = 0.03
num_epochs = 3
# 定义的模型名称，便于以后换模型
net = linreg
# 定义的模型损失名称，便于以后换损失函数
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # `X`和`y`的小批量损失
        # 因为`l`形状是(`batch_size`, 1)，而不是一个标量。`l`中的所有元素被加到一起，
        # 并以此计算关于[`w`, `b`]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

'''
epoch 1, loss 0.043538
epoch 2, loss 0.000165
epoch 3, loss 0.000050
'''

loss.sum().backward()中对于sum()的理解
pytorch backward() 的一点简单的理解

3.8 比较参数

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
'''
w的估计误差: tensor([0.0010, 0.0004], grad_fn=)
b的估计误差: tensor([2.0504e-05], grad_fn=)
'''

4 线性回归的简洁实现

4.1 生成数据集

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

4.2 读取数据集

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    # TensorDataset将输入的两类数据进行一一对应
    # * 表示对Tuple解包入参
    dataset = data.TensorDataset(*data_arrays)
    # DataLoader重新排序
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

# 这里我们使用iter构造Python迭代器，并使用next从迭代器中获取第一项.
next(iter(data_iter))
'''
[tensor([[-0.6054, -0.8844],
         [-0.7336,  1.4959],
         [ 0.0251, -0.5782],
         [-0.3874, -2.7577],
         [-0.2987, -1.6454],
         [-1.6794,  0.9353],
         [-1.1240,  0.0860],
         [ 0.7230, -0.3869],
         [ 0.2812, -1.3614],
         [ 1.4122,  0.7235]]),
 tensor([[ 5.9993],
         [-2.3407],
         [ 6.2172],
         [12.8106],
         [ 9.2043],
         [-2.3530],
         [ 1.6639],
         [ 6.9765],
         [ 9.3874],
         [ 4.5664]])]
'''

4.3 定义模型

# `nn` 是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

'''
nn.Sequential：可以看出list of layers，是一个有序的容器，神经网络模块将按照在传入构造器的顺序依次被添加到计算图中执行，同时以神经网络模块为元素的有序字典也可以作为传入参数。

'''

pytorch系列7 -----nn.Sequential讲解

4.4 初始化模型参数

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
'''
tensor([0.])
'''

4.5 定义损失函数

loss = nn.MSELoss()

4.6 定义优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

4.7 训练

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

'''
epoch 1, loss 0.000254
epoch 2, loss 0.000098
epoch 3, loss 0.000098
'''

4.8 比较参数

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

'''
w的估计误差： tensor([0.0007, 0.0007])
b的估计误差： tensor([-0.0007])
'''